TIL 16) DFS & BFS with Javascript

1. DFS

dfs는 깊이 우선 탐색이라고 하며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.

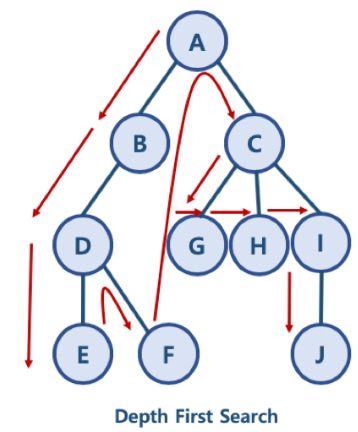
1-1) 스택을 이용한 DFS 구현

탐색을 마친 노드와 탐색이 필요한 노드를 각각 배열로 선언한다.

첫 번째 노드를 탐색이 필요한 노드에 push 하면서 탐색이 시작된다.

탐색이 필요한 노드가 없어질 때까지 탐색을 계속한다.

const graph = {
  A: ["B", "C"],
  B: ["A", "D"],
  C: ["A", "G", "H", "I"],
  D: ["B", "E", "F"],
  E: ["D"],
  F: ["D"],
  G: ["C"],
  H: ["C"],
  I: ["C", "J"],
  J: ["I"],
};


const dfs1 = (graph, startNode) => {
  const visited = []; // 탐색을 마친 노드
  let needVisit = []; // 탐색이 필요한 노드

  needVisit.push(startNode); // 탐색 시작

  while (needVisit.length > 0) {
    // 탐색이 필요한 노드가 0이 될때까지 반복
    const node = needVisit.shift(); // pop과 shift로 어디 방향부터 탐색할 지 정한다. shift는
    if (!visited.includes(node)) {
      // 탐색을 마친 노드에 없다면?
      console.log(`탐색을 마친 노드 node ${node}`);
      visited.push(node); //탐색을 마쳤으므로 탐색을 마친 노드에 넣어줌
      needVisit = [...graph[node], ...needVisit];
      console.log(`다음 탐색할 노드인 needVisit : ${needVisit}`);
    }
  }
  return visited;
};


// output
탐색을 마친 노드 node A
다음 탐색할 노드인 needVisit : B,C
탐색을 마친 노드 node B
다음 탐색할 노드인 needVisit : A,D,C
탐색을 마친 노드 node D
다음 탐색할 노드인 needVisit : B,E,F,C
탐색을 마친 노드 node E
다음 탐색할 노드인 needVisit : D,F,C
탐색을 마친 노드 node F
다음 탐색할 노드인 needVisit : D,C
탐색을 마친 노드 node C
다음 탐색할 노드인 needVisit : A,G,H,I
탐색을 마친 노드 node G
다음 탐색할 노드인 needVisit : C,H,I
탐색을 마친 노드 node H
다음 탐색할 노드인 needVisit : C,I
탐색을 마친 노드 node I
다음 탐색할 노드인 needVisit : C,J
탐색을 마친 노드 node J
다음 탐색할 노드인 needVisit : I
[
  'A', 'B', 'D', 'E',
  'F', 'C', 'G', 'H',
  'I', 'J'
]

1-2) 재귀를 이용한 DFS 구현

스택을 계속해서 반복하는 것과 비슷하게 재귀도 구현하면 된다.

방문하지 않은 노드만을 찾아서 dfs함수를 다시 호출하여 실행한다.

// 그래프는 위와 같음

let visited = [];
const dfs2 = (graph, start) => {
  if (!visited.includes(start)) {
    // 방문하지 않은 노드만 탐색
    visited.push(start);
    for (let i = 0; i < graph[start].length; i++) {
      dfs2(graph, graph[start][i]); 
      // 해당 노드의 자식,부모 모두 dfs2의 param으로 전달해서 재호출한다.
    }
  }
};

dfs2(graph, "A");
console.log(visited);

// output
[
  'A', 'B', 'D', 'E',
  'F', 'C', 'G', 'H',
  'I', 'J'
]

2. BFS

BFS는 Breadth Frist Search의 약자로 넓이 우선 탐색이다.

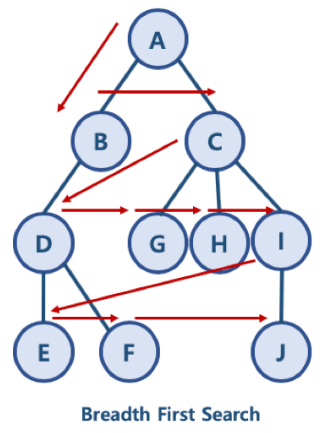
2-1) BFS를 큐로 구현

const Bfs = (graph, startNode) => {
  const visited = []; // 탐색을 마친 노드
  let needVisit = []; // 탐색이 필요한 노드

  needVisit.push(startNode); // 탐색 시작

  while (needVisit.length > 0) {
    // 탐색이 필요한 노드가 0이 될때까지 반복
    const node = needVisit.shift(); // pop과 shift로 어디 방향부터 탐색할 지 정한다. shift는
    if (!visited.includes(node)) {
      // 탐색을 마친 노드에 없다면?
      console.log(`탐색을 마친 노드 node ${node}`);
      visited.push(node); //탐색을 마쳤으므로 탐색을 마친 노드에 넣어줌
      needVisit = [...needVisit, ...graph[node]];
      //console.log(`need Visit : ${needVisit}`);
      console.log(`다음 탐색할 노드의 집합인 needVisit : ${needVisit}`);
      console.log(
        `추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:${graph[node]}`
      );
      console.log("=======");
    }
  }
  return visited;
};
console.log(Bfs(graph, "A"));


// output
탐색을 마친 노드 node A
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:B,C
다음 탐색할 노드의 집합인 needVisit : B,C
=======
탐색을 마친 노드 node B
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:A,D
다음 탐색할 노드의 집합인 needVisit : C,A,D
=======
탐색을 마친 노드 node C
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:A,G,H,I
다음 탐색할 노드의 집합인 needVisit : A,D,A,G,H,I
=======
탐색을 마친 노드 node D
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:B,E,F
다음 탐색할 노드의 집합인 needVisit : A,G,H,I,B,E,F
=======
탐색을 마친 노드 node G
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:C
다음 탐색할 노드의 집합인 needVisit : H,I,B,E,F,C
=======
탐색을 마친 노드 node H
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:C
다음 탐색할 노드의 집합인 needVisit : I,B,E,F,C,C
=======
탐색을 마친 노드 node I
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:C,J
다음 탐색할 노드의 집합인 needVisit : B,E,F,C,C,C,J
=======
탐색을 마친 노드 node E
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:D
다음 탐색할 노드의 집합인 needVisit : F,C,C,C,J,D
=======
탐색을 마친 노드 node F
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:D
다음 탐색할 노드의 집합인 needVisit : C,C,C,J,D,D
=======
탐색을 마친 노드 node J
추가 탐색을 위해 needVisit에 들어가야할 ...graph[node]:I
다음 탐색할 노드의 집합인 needVisit : D,D,I
=======
[
  'A', 'B', 'C', 'D',
  'G', 'H', 'I', 'E',
  'F', 'J'
]

3. 예제

사실 이번 TIL은 코드스테이츠의 코플릿에 있는 DFS/BFS 문제를 풀면서 작성하였다.

기존에는 DFS/BFS의 개념만 알고있었을 뿐, 이렇게 상세히 구현은 해본 적이 없다.

코플릿에서의 문제는 다음과 같다.

문제

let bfs = function (node) {
  // TODO: 여기에 코드를 작성합니다.
};
// 이 아래 코드는 변경하지 않아도 됩니다. 자유롭게 참고하세요.
let Node = function (value) {
  this.value = value;
  this.children = [];
};
// 위 Node 객체로 구성되는 트리는 매우 단순한 형태의 트리입니다.
// membership check(중복 확인)를 따로 하지 않습니다.
Node.prototype.addChild = function (child) {
  this.children.push(child);
  return child;
};

입출력 예시

let root = new Node(1);
let rootChild1 = root.addChild(new Node(2));
let rootChild2 = root.addChild(new Node(3));
let leaf1 = rootChild1.addChild(new Node(4));
let leaf2 = rootChild1.addChild(new Node(5));
let output = bfs(root);
console.log(output); // --> [1, 2, 3, 4, 5]
leaf1.addChild(new Node(6));
rootChild2.addChild(new Node(7));
output = bfs(root);
console.log(output); // --> [1, 2, 3, 4, 5, 7, 6]

BFS만 예로 들어보겠다. 위에 작성한 것처럼 TODO도 동일한 로직으로 작성하면 된다.

let bfs = function (node) {
    let visited = [];
  let needVisited = [];
  visited.push(node.value);
  needVisited = [...node.children];
  while(needVisited.length>0){
    const visitnode = needVisited.shift(); // 방문 배열의 맨 앞에서 하나 추출
    visited.push(visitnode.value);
    needVisited = [...needVisited,...visitnode.children];
  }