자료 구조 - 힙(heapq)

힙은 특정한 규칙을 가지는 트리로, 최댓값과 최솟값을 찾는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한다.

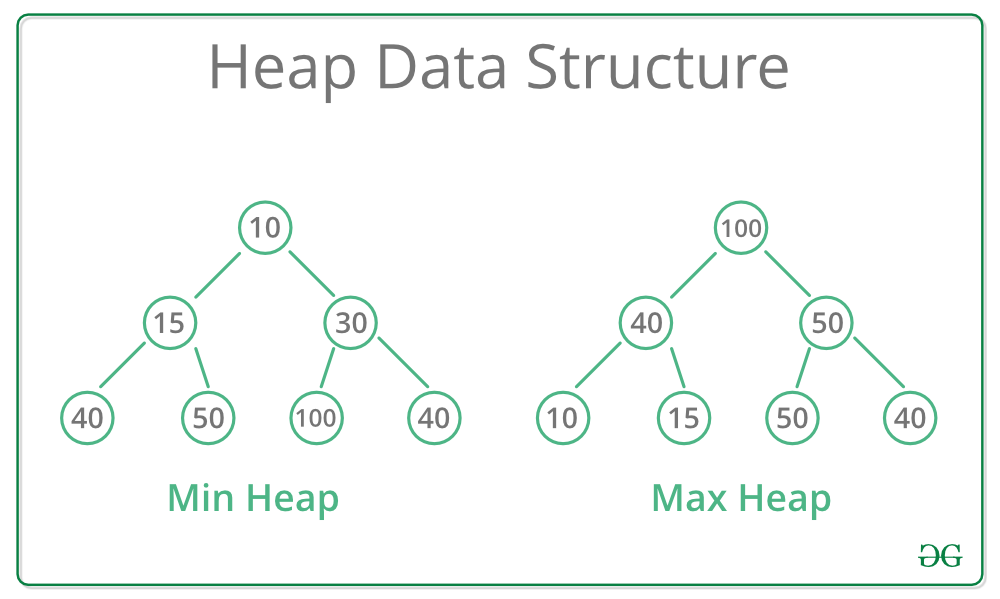
힙 property

부모노드와 자식모드의 키값 사이에는 대소 관계가 성립된다.

• 최소 힙: 부모 노드의 키값이 자식 노드의 키값보다 항상 작은 힙
• 최대 힙: 부모 노드의 키값이 자식 노드의 키값보다 항상 큰 힙

파이썬 힙 자료구조 heapq 모듈

파이썬 heapq 모듈은 내장 모듈로 heapq (priority queue) 알고리즘을 제공한다.
모든 부모 노드는 그의 자식 노드보다 값이 작거나 큰 이진트리(binary tree) 구조인데, 내부적으로는 인덱스 0에서 시작해 k번째 원소가 항상 자식 원소들(2k+1, 2k+2) 보다 작거나 같은 최소 힙의 형태로 정렬된다.

힙 함수 활용하기

• heapq.heappush(heap, item) : item을 heap에 추가

import heapq
heap = []
heapq.heappush(heap, 50)
heapq.heappush(heap, 10)
heapq.heappush(heap, 20)
print(heap)
# [10, 50, 20]

• heapq.heappop(heap) : heap에서 가장 작은 원소를 pop & 리턴. 비어 있는 경우 IndexError가 호출됨.

result = heapq.heappop(heap)

print(result)
print(heap)

# 10
# [20, 50]

• heapq.heapify(x) : 리스트 x를 즉각적으로 heap으로 변환함 (in linear time, O(N) )

heap2 = [50 ,10, 20]
heapq.heapify(heap2)
print(heap2)
# [10, 50, 20]

최대 힙 만들기
파이썬의 heapq 모듈은 최소 힙으로 구현되어 있기 때문에 최대 힙 구현을 위해서는 트릭이 필요하다.
바로 y = -x 변환을 하여 최솟값 정렬이 최댓값 정렬로 바꾸는 것이다.

힙에 원소를 추가할 때 (-item, item)의 튜플 형태로 넣어주면 튜플의 첫 번째 원소를 우선순위로 힙을 구성하게 된다. 이때 원소 값의 부호를 바꿨기 때문에, 최소 힙으로 구현된 heapq 모듈을 최대 힙 구현에 활용하게 되는 것이다.

아래의 예시는 리스트 heap_items에 있는 원소들을 max_heap이라는 최대 힙 자료구조로 만드는 코드이다.

import heapq
heap_items =[1,3,5,7,9]
max_heap = []
for item in heap_items:
    heapq.heappush(max_heap, (-item, item))
print(max_heap)
# [(-9, 9), (-7, 7), (-3, 3), (-1, 1), (-5, 5)]