미분으로 함수값 추론하기
함수증가
미분값을 더해주면 함수는 증가하게 됩니다.
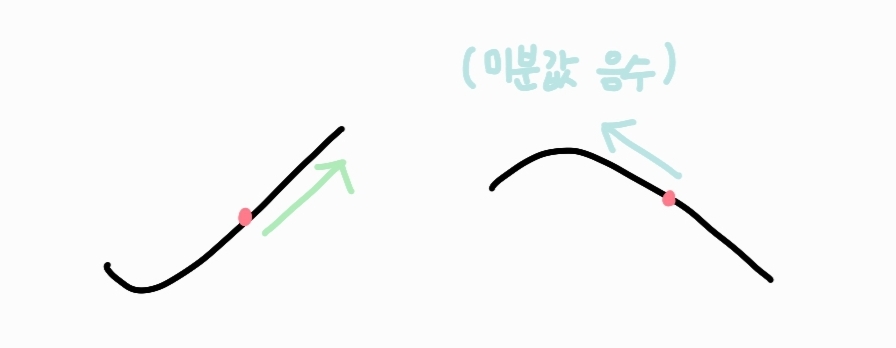
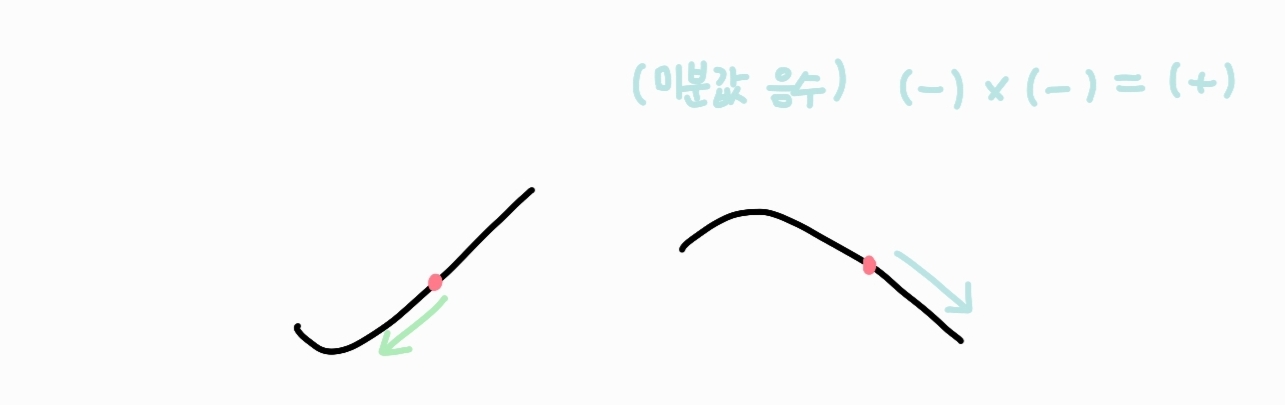
함수감소
미분값을 빼주면 함수는 감소하게 됩니다.
경사하강법으로 선형회귀 계수 구하기
선형모델의 경우 아래 식과 같이 역행렬을 이용하여 회귀분석이 가능했습니다.
이제 역행렬을 이용하지 않고 경사하강법을 이용하여 적절한 선형모델을 찾아보도록 하겠습니다.
선형회귀의 목적은 norm 를 최소화하는 를 찾는 것 입니다. 따라서 다음과 같은 그레디언트 벡터를 구해야합니다.
다음과 같이 치환하여 미분을 하게 되면,
다음과 같은 식을 구할 수 있습니다.
💻 알고리즘
경사하강법 기반 선형회귀 알고리즘은 다음과 같은 코드로 나타낼 수 있습니다.
for i in range(T):
error = y - x @ beta
grad = - transpose(X) @ error
beta = beta - lr * grad경사하강법은 만능일까?
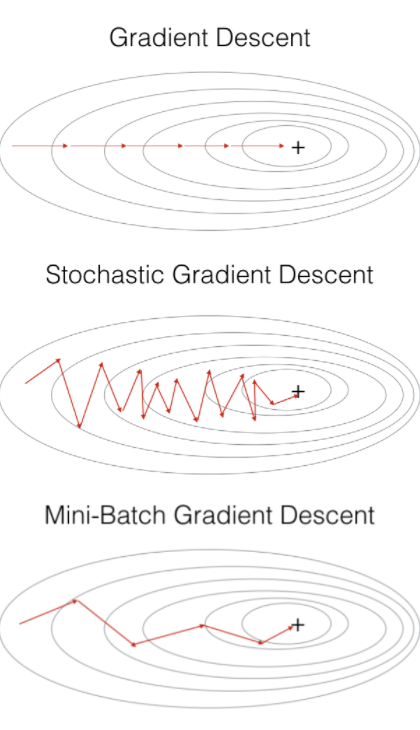
이론적으로 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해서 수렴이 보장됩니다.
그렇기 때문에 비선형회귀 문제의 경우 목적식이 볼록하지 볼록하지 않을 수 있으므로 수렴이 항상 보장된다고는 할 수 없습니다.

확률적 경사하강법(Stochastic Gradient Descent:SGD)
볼록이 아닌(non-convex) 목적식에서 경사하강법을 사용할 때 쓰이는 방법입니다. 모든 데이터를 이용하여 파라미터를 업데이트 하는 대신 데이터 한개 또는 일부를 활용하여 업데이트합니다. 따라서 연산자원을 좀 더 효율적으로 활용하는데 도움이 됩니다.
SGD는 batch_size = 1인 경사하강법을 말하며, 볼록이 아닌 목적식에서도 사용이 가능하므로 경사하강법보다 머신러닝 학습에 더 효율적이라고 할 수 있습니다.

미니배치 확률적 경사하강법 (Mini-Batch Stochastic Gradient Descent: MSGD)
MSGD는 전체 데이터를 batch_size개 씩 나눠 배치로 학습 하는 방식을 말합니다. 여기서 batch_size는 사용자가 지정할 수 있습니다.
예를 들어, 전체 데이터가 1000개라고 하고, batch_size를 10으로 지정한다면, 전체를 100개씩 총 10 묶음의 배치로 나누어 1 Epoch당 10번 경사하강법을 진행합니다.