[Algorithm & DS] 최소 신장 트리 (MST, Minimum Spanning Tree)

✅ Spanning Tree

✏️ Spanning Tree란

그래프 내의 모든 정점을 포함하는 트리

• Spanning Tree == 신장 트리 == 스패닝 트리
• Spanning Tree는 그래프의 최소 연결 부분 그래프 이다.
  • 최소 연결 : 간선의 수가 가장 적다.
  • n개의 정점을 가지는 그래프의 최소 간선의 수는 (n-1)개 이고, (n-1)개의 간선으로 연결되어 있으면 필연적으로 트리 형태가 되고 이것이 바로 Spanning Tree가 된다.
• 즉, 그래프에서 일부 간선을 선택해서 만든 트리

✏️ Spanning Tree의 특징

• DFS/BFS를 이용하여 그래프에서 신장 트리를 찾을 수 있다.
  • 탐색 도중에 사용된 간선만 모으면 만들 수 있다.
• 하나의 그래프에는 많은 신장 트리가 존재할 수 있다.
• Spanning Tree는 트리의 특수한 형태이므로 모든 정점들이 연결되어 있어야 하고, 사이클을 포함해서는 안된다.
• 따라서, Spanning Tree는 그래프에 있는 n개의 정점을 정확히 (n-1)개의 간선으로 연결한다.

✏️ Spanning Tree의 사용 사례

• 통신 네트워크 구축
  

  • 예를 들어, 회사 내의 모든 전화기를 가장 적은 수의 케이블을 사용하여 연결하고자 하는 경우
  • n개의 위치를 연결하는 통신 네트워크를 최소의 링크(간선)를 이용하여 구축하고자 하는 경우, 최소 링크의 수는 (n-1)개가 되고, 따라서 Spanning Tree가 가능해진다.

✅ 최소 신장 트리 (MST, Minimum Spanning Tree)

✏️ 최소 신장 트리(MTS)란

Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리

• MST == Minimum Spanning Tree == 최소 신장 트리
• 각 간선의 가중치가 동일하지 않을때, 단순히 가장 적은 간선을 사용한다고 해서 최소 비용이 얻어지는 것은 아니다.
• MST는 간선의 가중치를 고려하여 최소 비용의 Spanning Tree를 선택하는 것을 말한다.
• 즉, 네트워크(가중치를 간선에 할당한 그래프)에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결하는 것이다.

✏️ 최소 신장 트리의 특징

1. 간선의 가중치의 합이 최소여야한다.
2. n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용해야 한다.
3. 사이클이 포함되어서는 안된다.

✏️ 최소 신장 트리의 사용 사례

통신망, 도로망, 유통망에서 길이, 구축 비용, 전송 시간 등을 최소로 구축하려는 경우

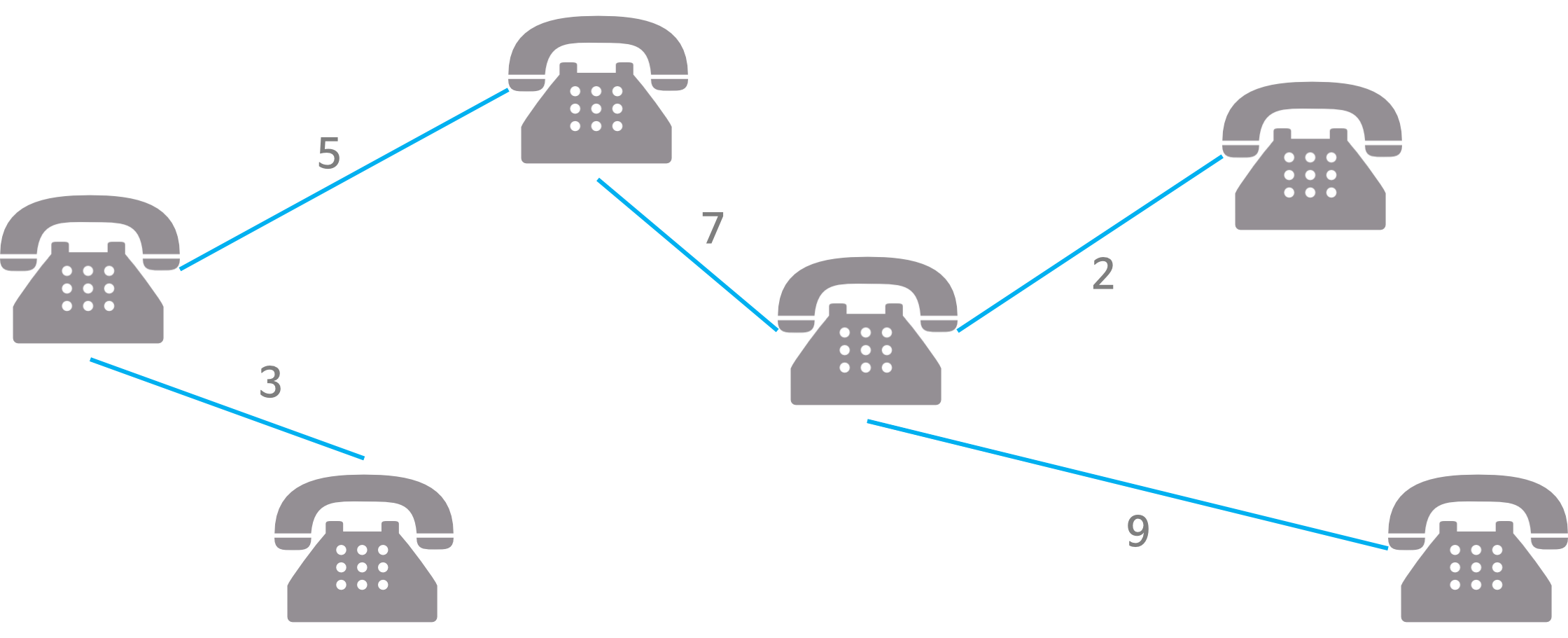
• 도로 건설
  • 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제
• 전기 회로
  • 단자들을 모두 연결하면서 전선의 길이가 최소가 되도록 하는 문제
• 통신
  • 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제
• 배관
  • 파이프를 모두 연결하면서 파이프의 총 길이가 최소가 되도록 연결하는 문제

✏️ 최소 신장 트리의 구현 방법

1. Kruskal 알고리즘

2. Prim 알고리즘