로지스틱 회귀
로지스틱 회귀(Logistic Regression)는 기계 학습과 통계 분야에서 사용되는 분류(classification) 알고리즘 중 하나. 이름은 회귀(regression)라는 용어가 들어가지만, 실제로는 분류 문제를 다룸. 이 알고리즘은 주로 두 개의 가능한 출력 클래스(이진 분류)를 예측하는 데 사용되며, 다중 클래스 분류로 확장할 수도 있음.
로지스틱 회귀의 핵심 아이디어는 입력 특성과 가중치(weight)를 사용하여 입력 데이터 포인트가 특정 클래스에 속할 확률을 예측하는 것. 이 예측은 로지스틱 함수(또는 시그모이드 함수)를 사용하여 0과 1 사이의 확률 값으로 변환됩니다. 로지스틱 함수는 S 모양의 곡선을 그리며, 입력값이 양수 무한대로 커지면 1에 수렴하고, 음수 무한대로 작아지면 0에 수렴. 이러한 특성으로 인해 로지스틱 회귀는 이진 분류에 적합.
로지스틱 회귀의 학습 과정은 주어진 데이터를 기반으로 최적의 가중치(계수)를 찾는 것을 포함. 이 학습 과정에서 일반적으로 로그-우도(log-likelihood)나 크로스 엔트로피 손실 함수와 같은 목적 함수를 최소화하는 방향으로 가중치를 조정.
로지스틱 회귀는 간단하면서 효과적인 분류 알고리즘이며, 다양한 분야에서 활발하게 사용. 예를 들면 의학 분야에서 질병 진단, 마케팅에서 고객 이탈 예측, 자연어 처리에서 텍스트 분류 등 다양한 응용 분야에서 활용됨
k최근접 이웃 분류기의 확률 예측
해당 데이터 들을 형식에 맞춰 준비해 놓은 후
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)이는 2장에서 훈련했던 것 처럼 사이킷 런의 이웃 객체를 만들고 훈련세트 모델을 훈현한 다음 훈련 세트와 테스트 세트의 점수를 확인해 보겠다. 최근접 이웃의 갯수를 3으로 지정하여 사용해 보았다.
print(kn.predict(test_scaled[:5])) 테스트 케이스에 있는 5개의 타깃 값을 예측해 보았다.
이는
import numpy as np
proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals = 4))위와 같은 코드를 통해 확률을 계산하고 그 확률에 맞춰서 예측을 해준다.

distances, indexes = kn.kneighbors(test_scaled[3:4])
print(train_target[indexes])위를 통해 해당 테스트케이스의 확률이 가장 가까운 이웃의 비율이 맞는지 확인해 보자
로지스틱 회귀 이름은 회귀지만 분류모델을 말한다.
시그모이드 함수를 활용하여 이를 나타내는데 다음과 같은 예시로 시그모이드 함수를 만든다
import numpy as np
import matplotlib.pyplot as plt
z = np.arange(-5,5,0.1)
phi = 1/(1+np.exp(-z))
plt.plot(z,phi)
plt.xlabel('z')
plt.ylabel('phi')
plt.show()위는 -5부터 5까지의 z값을 0.1 마다 계산하여 함수로 만든것을 의미하고 아래와 같은 결과를 얻을 수 있다.
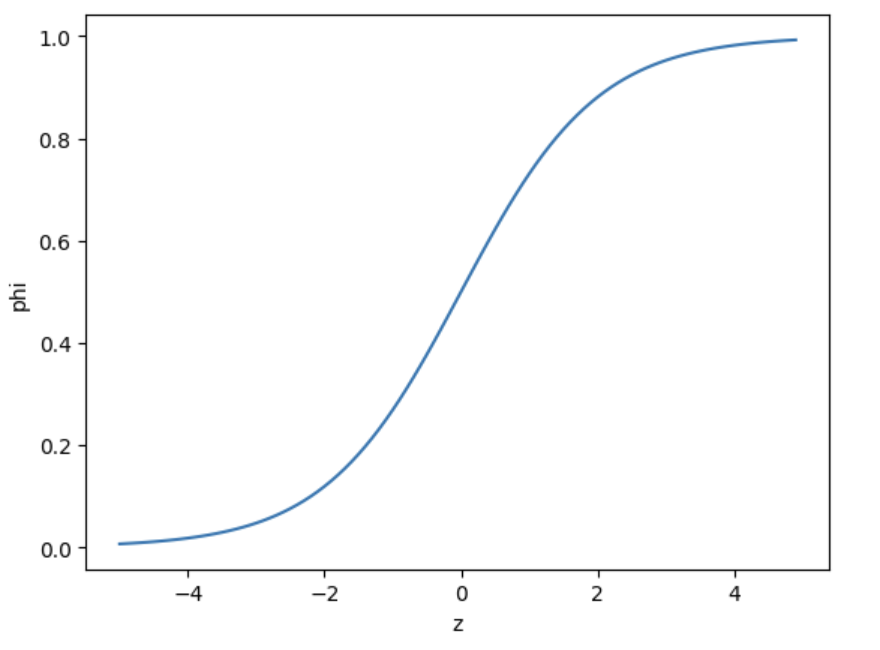
로지스틱 회귀로 이진 분류 수행하기
char_arr = np.array(['A','B','C','D','E'])
print(char_arr[[True,False,True,False,False]])위와 같은 방식으로 도미와 빙어 행만 골라보자
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]이제 이 데이터로 로지스틱 회귀 모델을 훈련해 보자
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)
print(lr.predict(train_bream_smelt[:5]))

두번째 샘플을 제외하고는 모두 도미로 예측했다.위의 로지스틱 회귀 또한 예측 메서드를 제공한다.
print(lr.predict_proba(train_bream_smelt[:5]))
알파벳 순서대로나열 된다
첫번째 요소는 도미, 두번째 요소는 빙어
print(lr.coef_,lr.intercept_)
decisions = lr.decision_function(train_bream_smelt[:5])
print(decisions)위는 로지스틱 회귀가 학습한 계수를 확인해보고
logisticRegression모델로 z 값을 계산해 본것이다

이제 z 값을 시그모이드 함수를 통과 시키면
from scipy.special import expit
print(expit(decisions))확률을 얻을 수 있다.
이제 이진분류를 바탕으로 7개의 생선을 분류하는 다중 분류로 넘어가겠습니다.
로지스틱 회귀 다중 분류 수행하기
lr = LogisticRegression(C = 20,max_iter = 1000)
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled,train_target))
print(lr.score(test_scaled,test_target))
훈련세트와 테스트 세트에 대해 점수가 높고 과대,과소 적합에 치우쳐져 있지 않으니 예측을 출력해보자
print(lr.predict(test_scaled[:5]))이제 테스트 세트의 처음 5개 샘플에 대한 예측 확률을 출력해보자. 출력을 간소하게 하기 위해 소수점 네자리에서 반올림 하겠다.
proba = lr.predict_proba(test_scaled[:5])
print(np.round(proba, decimals = 3))
선형 방정식의 모습을 확인해보자
print(lr.coef_.shape, lr.intercept_.shape)그 후 소프트 맥스 함수를 사용해 확률로 바꾸어 보자
decision = lr.decision_function(test_scaled[:5])
print(np.round(decision, decimals = 2))
from scipy.special import softmax
proba = softmax(decision, axis = 1)
print(np.round(proba, decimals = 3))


