Model Evaluation and Regularization

Evaluation → selection

Regularization → overfitting

Clustering Model Evaluation

clustering에서는 # of cluster을 명시해야 한다. (cluster의 개수 ..)

Clustering에서 Model Evaluation은 Cluster의 개수를 결정하는 것을 의미한다.

K-means에서는 inertia와 silhouette score / coefficient의 방법이 있다.

Inertia

Inertia란 거리의 제곱을 평균을 낸 값을 의미하며, 거리는 각각의 sample과 각 sample이 속해있는 centroid의 거리이다. 이는 k-means clustering에서 minimizing cost를 의미한다.

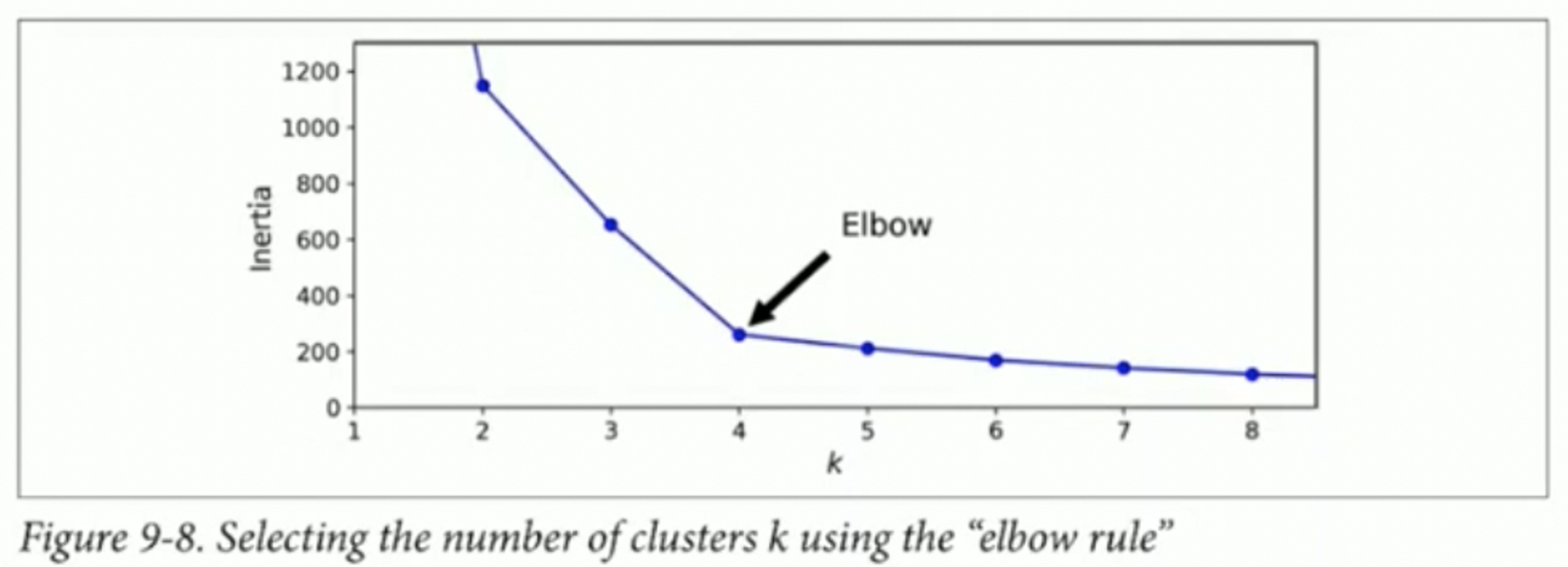
x축으로는 cluster의 개수를, 세로축으로는 inertia를 그렸을 때, 변화하는 기준점을 Elbow 라고 하고, 해당 Elbow가 각 클러스터의 개수를 정하는 한계점으로 정한다.

Silhouette score

각각의 sample에 대해 silhouette coefficient를 구해서 해당 값들의 평균을 silhouette score라고 한다.

silhouette score를 구하기 위해서는 intra-cluster distance와 nearest-cluster distance를 구해야 한다.

Intra-cluster distance는 sample에 대해서 같은 cluster에 속해있는 다른 sample들 과의 거리의 평균을 의미한다.

Nearest-cluster distance는 sample에 대해 다른 cluster 중 가장 가까운 cluster에 속해있는 sample들 과의 거리의 평균을 의미한다.

여기서 silhouette coefficient는 nearest-cluster disance에서 intra-cluster distance를 뺀 값에 둘 중 더 큰 값으로 나눈 값을 silhouette coefficient라고 한다.

기준이 되는 sample 해당 sample이 속한 cluster에 가까워 질수록 1의 값에 가까워지게 된다. 그런데 기준이 되는 sample이 두 cluster의 경계값에 위치한다면 0의 값에 가까워지게 된다. 기준이 되는 sample이 nearest cluster과 근접한 곳에 위치한다면 -1의 값에 가가워지게 된다. 이는 잘못된 cluster에 속해있는 경우라고 생각할 수도 있다.

수식으로 표현하자면 다음과 같다.

이 때, $a$는 intra-cluster distance의 평균, $b$는 nearest-cluster distance의 평균을 의미한다.

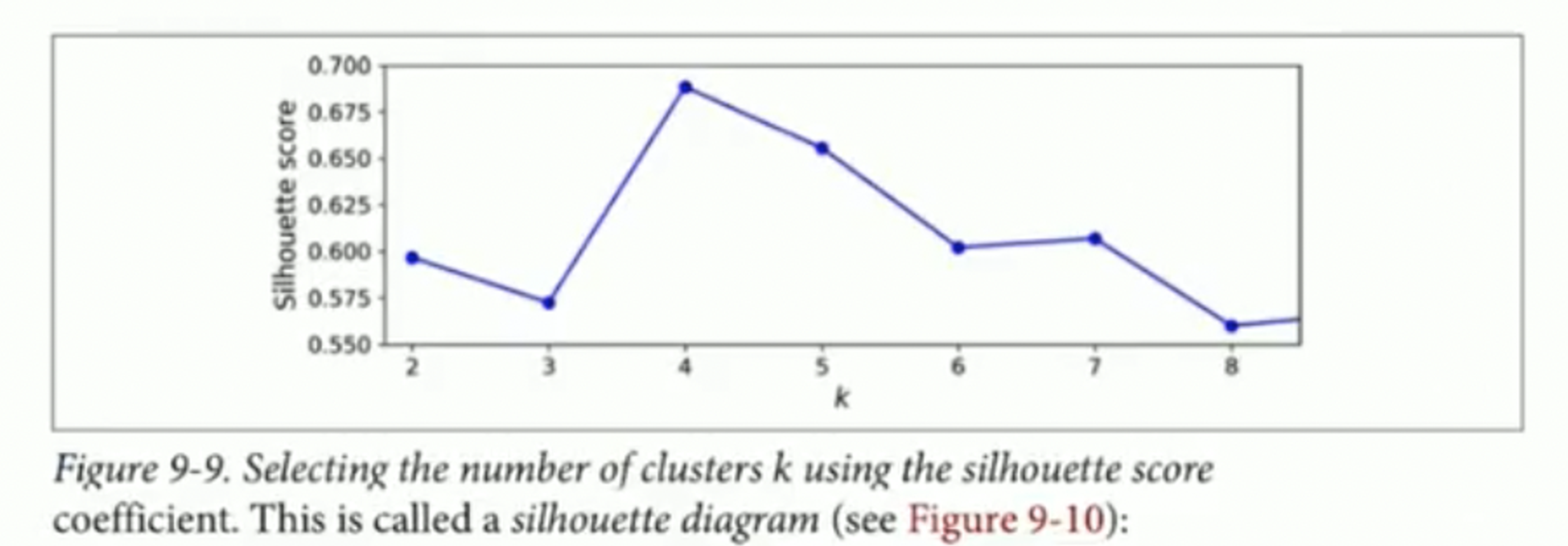
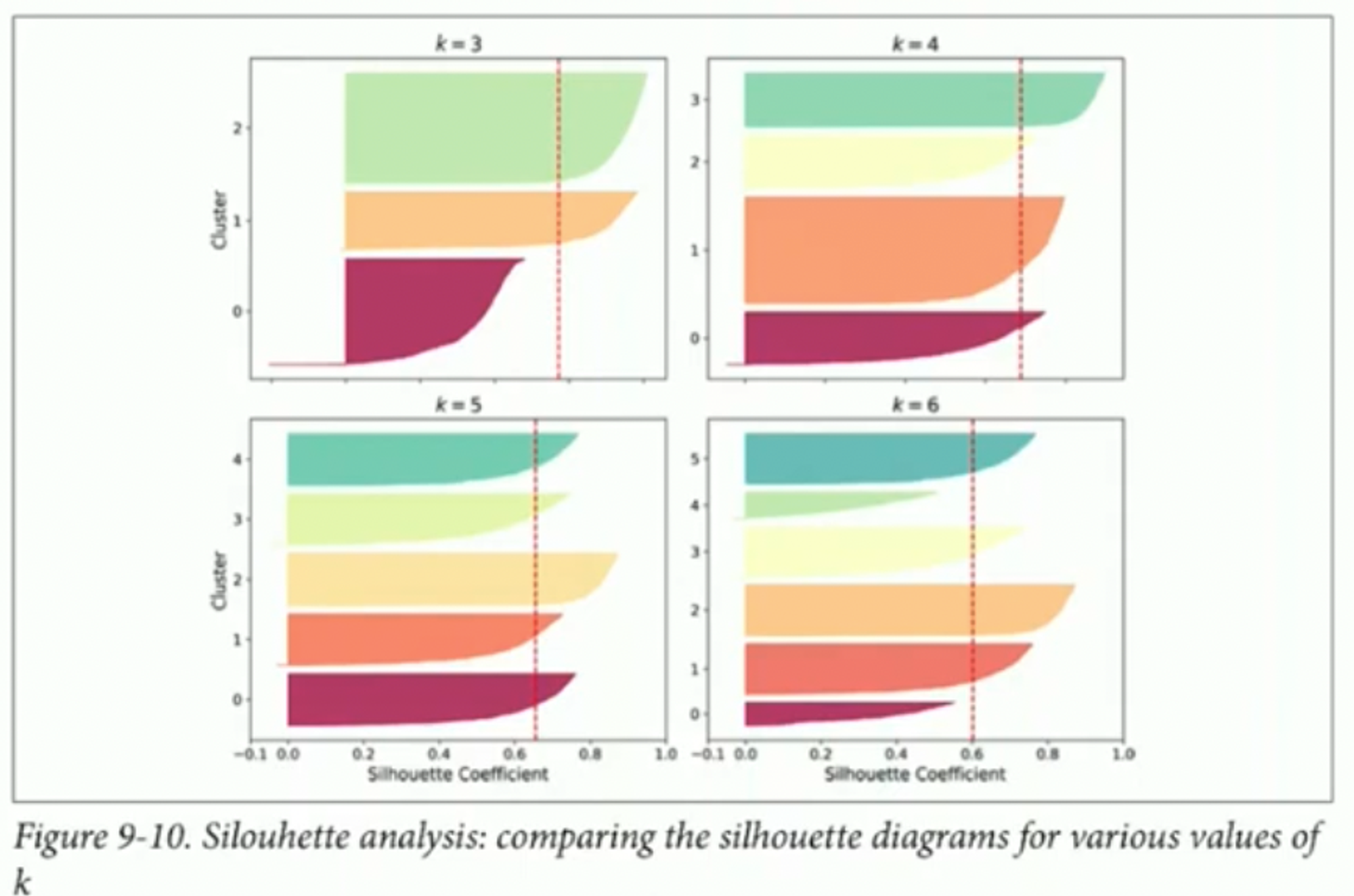
해당 그림은 cluster의 개수에 따라 silhouette coefficient를 표현한 그림이다. 해당 그림을 통해 silhouette coefficient의 분포를 확인할 수 있고, inertia보다 많은 정보를 담게 된다.

Polynomial Regression and Regularization

Polynomial은 다항식을 의미한다. 즉, 다항 회귀와 관련하여 알아보고, 해당 회귀에서 발생하는 과적합을 어떻게 줄일지 결정한다.

$y = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3$이라는 다항식이 존재할 때, 주어지는 input ($x$)를 바로 model에 입력하는 것이 아니라 feature를 추출하여 model에 입력하여 output ($y$)를 구하게 된다.

즉, model이 $y(z) = \theta_0 + \theta_1z_1 + \theta_2z_2 + \theta_3z_3$과 같은 형태로 나타내게 되는 것이다.

예를 들어 설명하겠다. $\mathbf{x} = \begin{bmatrix} 1 \space 2 \space 3 \space 4 \space 5\end{bmatrix}^T, \mathbf{y} = \begin{bmatrix} 4 \space 2 \space 1 \space 2 \space 4\end{bmatrix}^T$와 같은 값들이 존재한다고 한다면 다음과 같이 normal equation을 통해 구할 수 있다.

1차식인 경우 다음과 같이 파라미터를 바로 구할 수 있었다.

$\mathbf{x} = \begin{bmatrix} 1 \space 1 \\ 1 \space 2 \\ 1 \space 3 \\ 1 \space 4 \\ 1 \space 5\end{bmatrix}, \mathbf{y} = \begin{bmatrix} 4 \\ 2 \\ 1 \\ 2 \\ 4 \end{bmatrix}$, $\hat{\theta} = (\mathbf{x}^T\mathbf{x})^{-1}\mathbf{x}^T\mathbf{y}$이고, $y = \theta_0 + \theta_1x$로 모델이 나오게 된다.

2차로 모델을 확장하는 경우 모델은 $y = \theta_0 + \theta_1x + \theta_2x^2$이고 다음과 같이 normal equation을 구할 수 있다.

$\mathbf{x} = \begin{bmatrix} 1 \space 1 \space 1 \\ 1 \space 2 \space 4 \\ 1 \space 3 \space 9\\ 1 \space 4 \space 16\\ 1 \space 5 \space 25\end{bmatrix}, \mathbf{y} = \begin{bmatrix} 4 \\ 2 \\ 1 \\ 2 \\ 4 \end{bmatrix}$에 대해 $\hat{\theta} = (\mathbf{x}^T\mathbf{x})^{-1}\mathbf{x}^T\mathbf{y}$ 다음을 구하면 3 x 1의 parameter를 구할 수 있다.

마찬가지로 Batch Gradient Descent로 구한다면 다음과 같다.

$\theta = \theta - 2\eta\sum_{n=1}^{5}(\theta_0+\theta_1x+\theta_2x^2-y)\mathbf{x}_n$로 구할 수 있다.

Polynomial regression

모델의 차수(모델의 복잡도)는 어떻게 결정해야 할까?

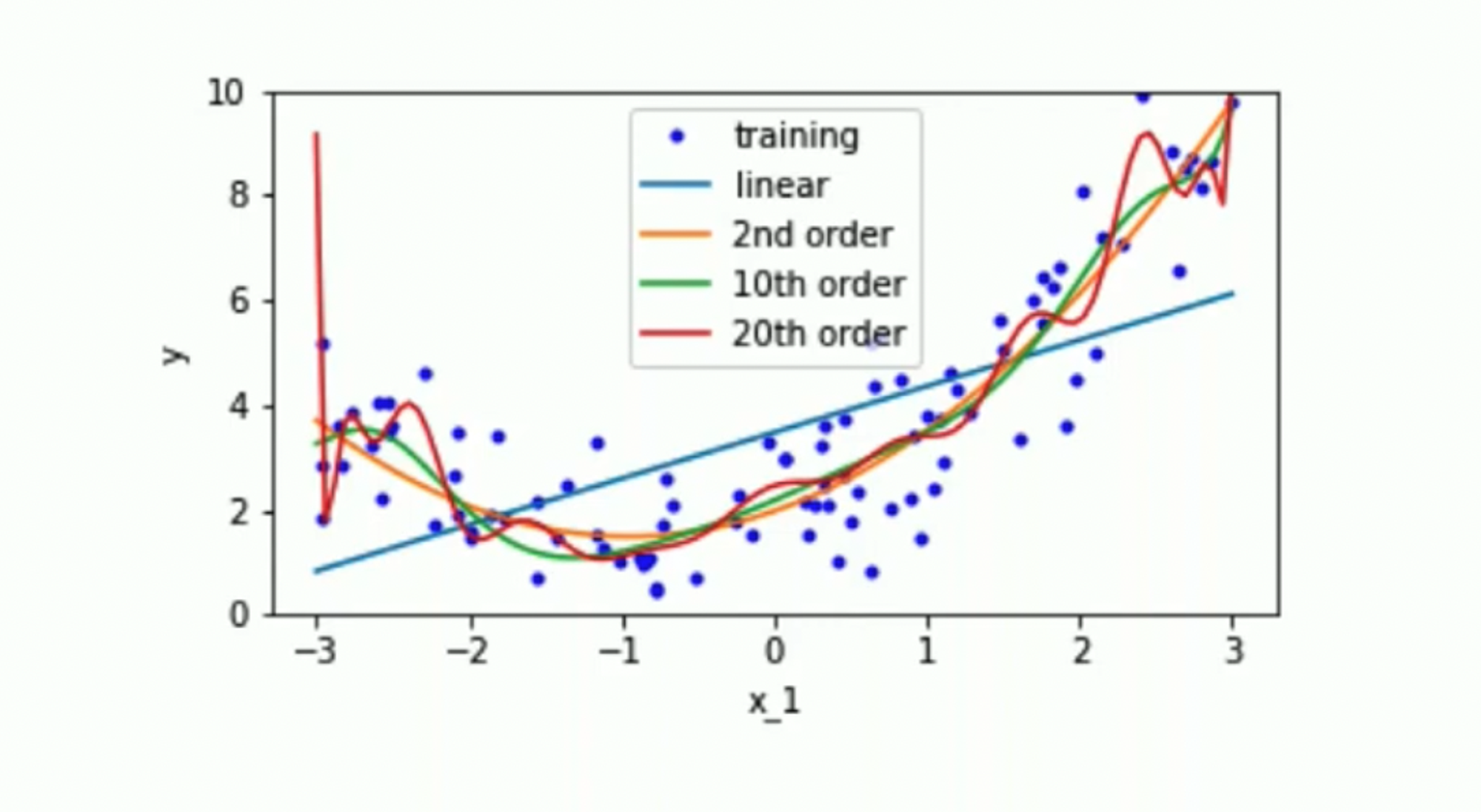
모델이 복잡해질수록 일반화 및 경향성을 다루지만 noise를 허용하지 않게 되는 현상이 존재한다. 이와 달리 모델이 단순화될수록 noise를 허용하게 되지만 경향성을 따르지 않게 된다.

Overfitting and Underfitting

overfitting

학습 데이터에 대해서는 좋은 성능을 보이지만, 처음 보는 데이터에 대해서는 일반화를 하지 못한다. 학습 데이터의 양이나 노이즈에 비해 모델이 너무 복잡할 때, 모델이 학습데이터를 일반화하는 범위를 넘어서 과도하게 의존하는 것이다.

underfitting

모델이 너무 단순화여 학습 데이터에 대해서도 부정확하다.

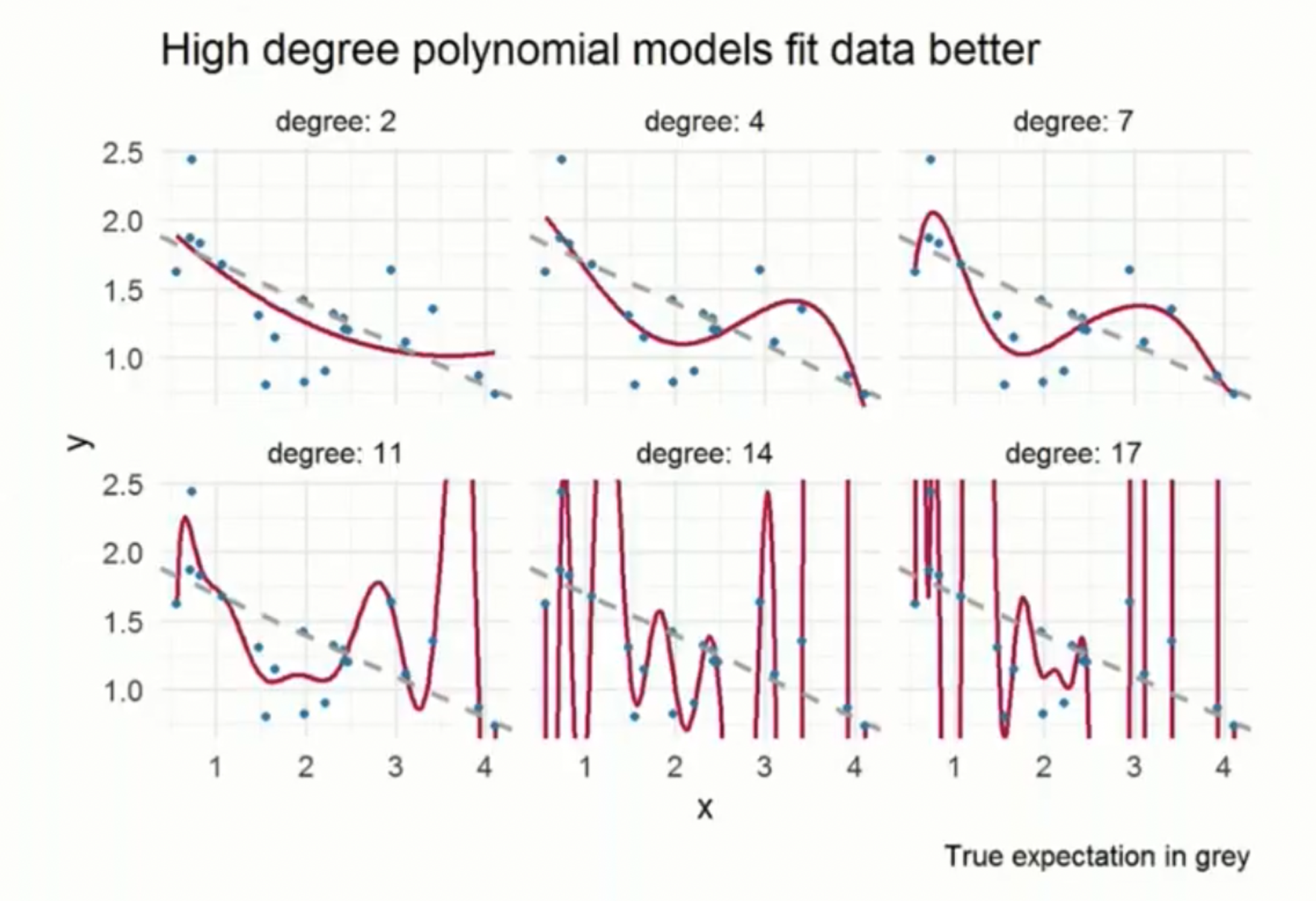
주어진 데이터가 있는 구간에서는 경향성을 따라가게 되지만, 데이터가 없는 구간은 예측을 통해 모델을 생성해야 한다. degree가 17인 경우 경향성을 따르지 않고 예측을 하여 과도한 모습을 보이고 있다.

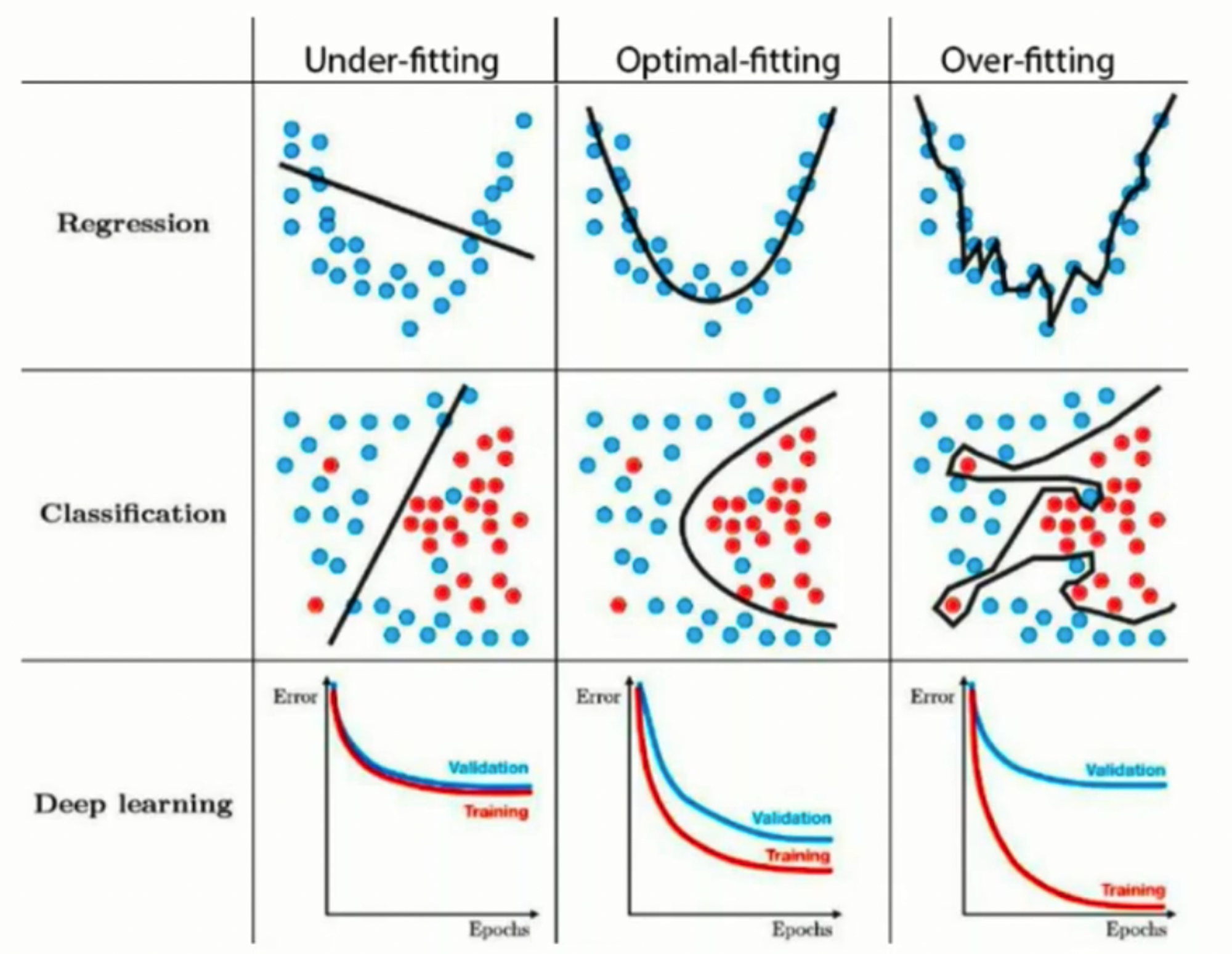
training 데이터에 대해서는 epoch이 늘어날 수록 error가 감소하지만, validation 혹은 test 데이터에 대해서는 그렇지 못한 모습을 보이는 경우 overfitting을 의심할 수 있다.

Regularization

정규화란 비용함수에 복잡도에대한 penalty를 추가하여 과적합에 대한 비용을 optimizing cost에 반영한 것을 의미한다.

Ridge regression

SSE와 parameter에는 trade-off이 존재한다. 위의 수식을 최소화하여 모델의 복잡도를 감소시키는 방법이다. 여기서 $\alpha$가 커지는 경우 parameter가 커지는 효과를 높여 모델을 더 단순하게 만들게 되고, 작아진다면 정규화가 작게된다. 즉, hyperparameter $\alpha$를 통해 두 항목 간의 상대적인 비중을 조절한다.

closed form solution은 $\hat{\theta} = (\mathbf{x}^T\mathbf{x}+\alpha\mathbf{I}_n)^{-1}\mathbf{x}^ty$이다.

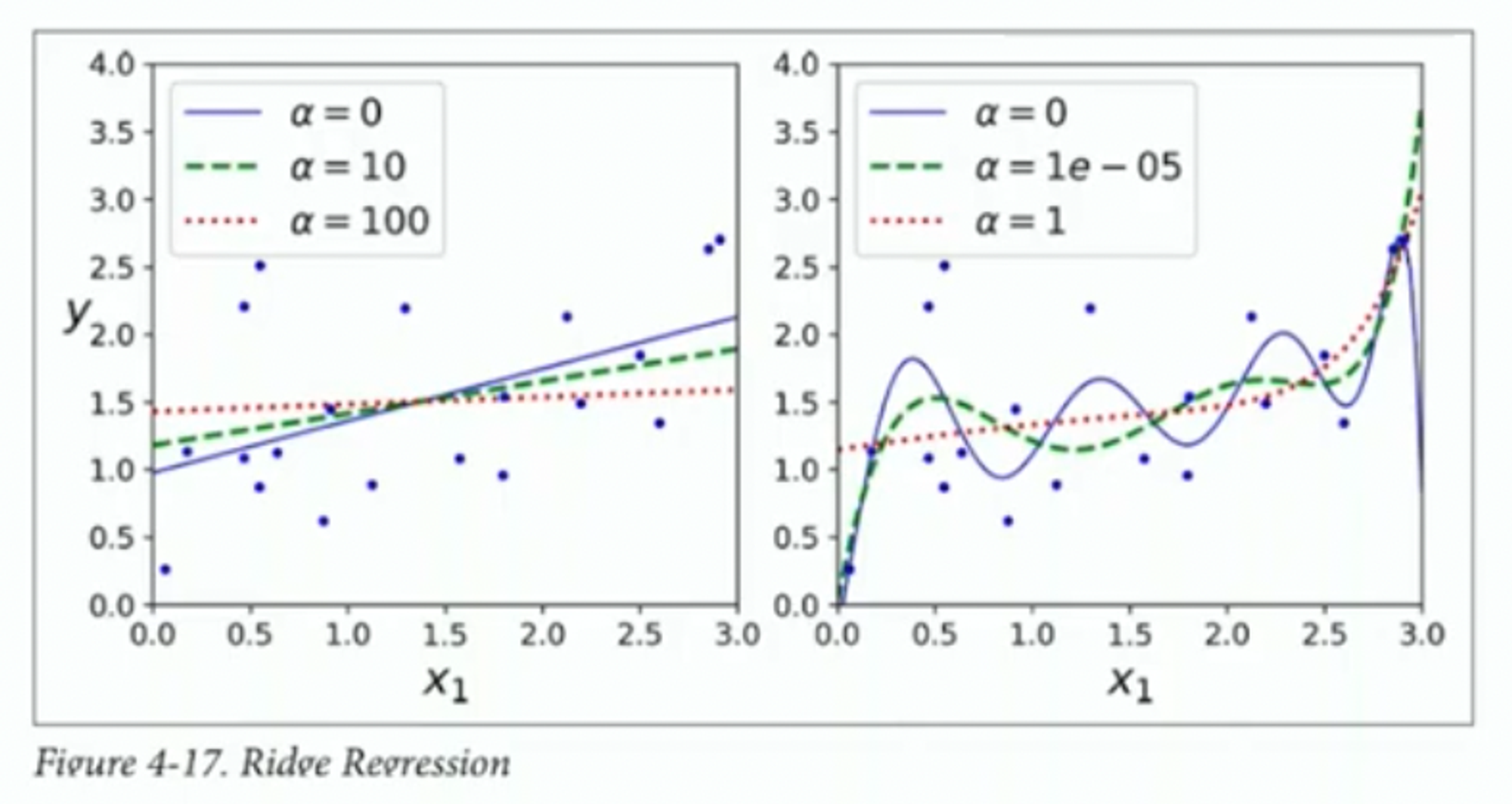
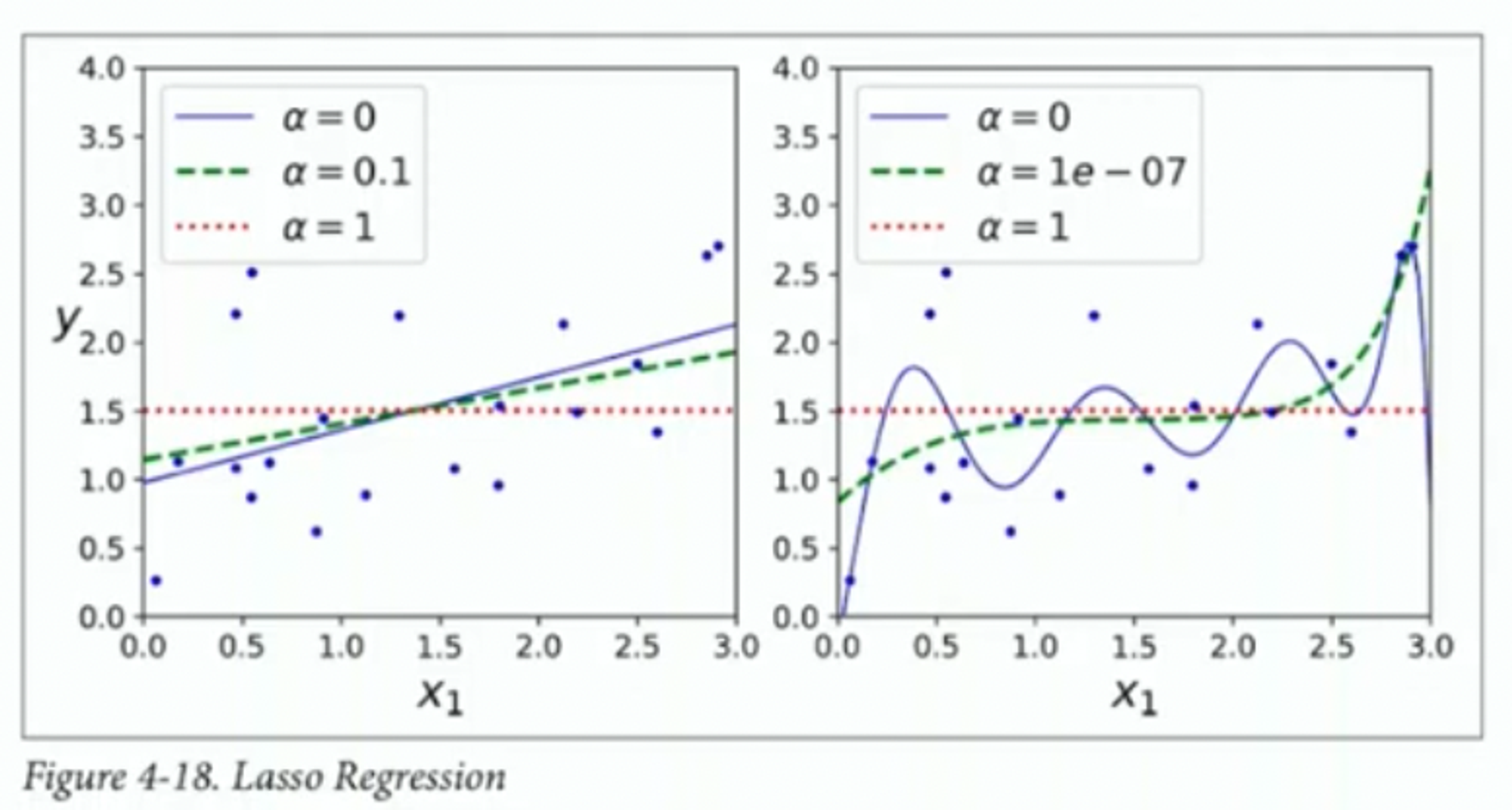
LASSO

Least Absolute Shrinkage and Selection Operator Regression으로 중요하지 않은 feature들의 weight를 0으로 만드는 경향이 있다.