K-Means Clustering

clustering ← unsupervised method ⇒ 입력만 존재함

입력 (sample) → clustering (군집화) → label 형태 (즉, 어떤 것들이 모여있다!)

k-means clustering이라고 하는 이유는 $x_1, x_2, ..., x_n$이라는 입력과 $k$라는 cluster의 개수를 입력해야하기 때문이다.

최종적으로 출력으로 나오는 것은 one-of-k coding으로 되어있는 label이 주어지는데, 우리는 이를 $R$이라고 하며, $N$ x $K$의 행렬로 표현이 된다.

k-means clustering에서는 중심 (centroid) 혹은 평균 (mean)으로 불리는 $k$개의 점을 사용하여 iterative 하게 동작한다.

주어진 sample과 어떤 시점의 주어진 $k$개의 중심을 통해 label을 계산한다. 그리고 해당 label과 sample을 통해 $k$개의 중심의 위치를 업데이트 한다. 이를 iterative하게 동작하도록 하는 방법이다.

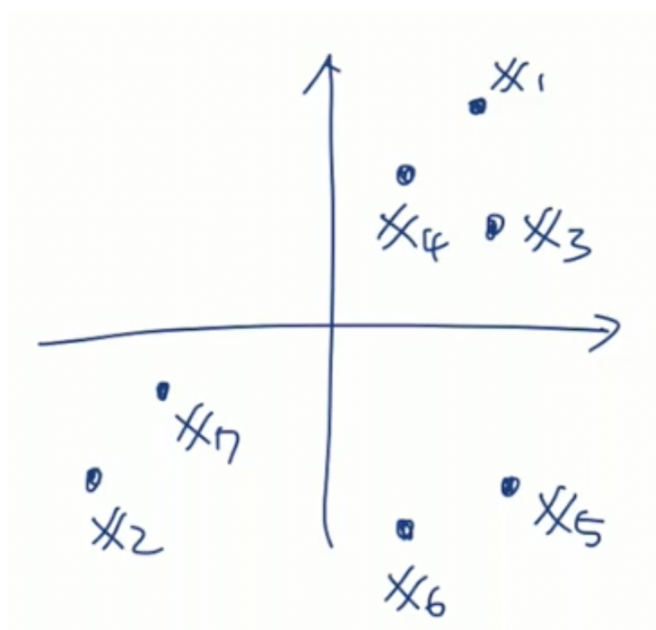
최초 다음과 같은 sample이 주어졌다고 하자. $k$개의 중심의 위치를 우리는 $\mu$라고 표현한다. $k$를 3이라고 지정했을 때, 최초 $\mu$의 위치를 다음과 같이 설정했다고 하자.

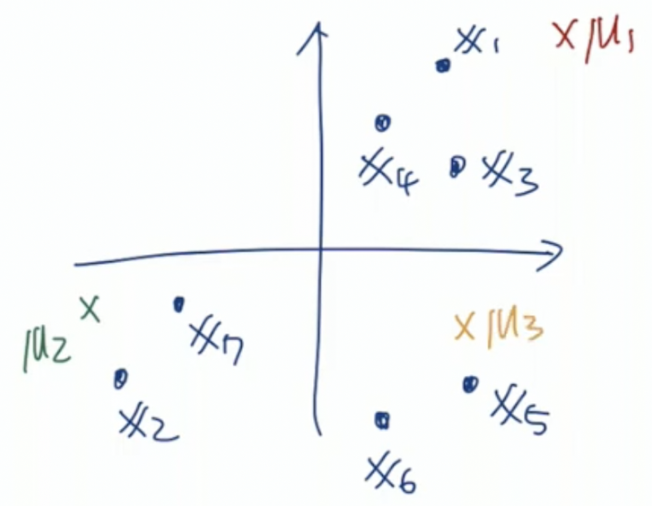
현재 sample의 개수는 7개이고, cluster의 개수는 3개이다. $R_{7 \mathbf{x} 3} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{bmatrix}$과 같이 label이 형성되게 된다.

주어진 sample $x_1, x_2, ..., x_7$과 주어진 centroid $\mu_1, \mu_2, \mu_3$을 통해 다음 label을 만들었다. 여기서 $\mu_1$과 가장 가깝다고 판단된 sample의 개수는 위 label에서 1열이 1인 값, 총 3개이다. $\mu_2, \mu_3$에 대해서도 같은 연산을 진행할 수 있다.

해당 시점에서 $\mu$을 업데이트 한다고 하자, $\mu_1 = \frac{1}{3}(x_1 + x_3 + x_4)$, $\mu_2 = \frac{1}{2}(x_2 + x_7)$, $\mu_3 = \frac{1}{2}(x_5 + x_6)$으로 업데이트 하면 된다.

이를 반복한다면 모여있다고 판단되는 군집의 중심으로 $\mu$들이 이동하게 된다.

$R = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 & 1 \\ \end{bmatrix}$이라는 label이 주어진다면, $\mu_1 = \frac{1}{2}(x_1 + x_3), \space \mu_2 = \frac{1}{2}(x_2 + x_4)$로 구할 수 있다.

혹은 $D_{5 \mathbf{x} 3} = \| x_n - \mu_n \|_2$인 $D = \begin{bmatrix} 1 & 4 & 9 \\ 2 & 5 & 6 \\ 8 & 2 & 7 \\ 6 & 1 & 9 \\ 10 & 5 & 1\\ \end{bmatrix}$이 주어졌을 때, 이를 통해 $R_{5 \mathbf{x} 3} = \begin{bmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$을 구할 수 있다.

어떻게? → $\mu$와 거리가 가장 가까운 값에 해당하는 $\mu$가 $R$값이 됨!

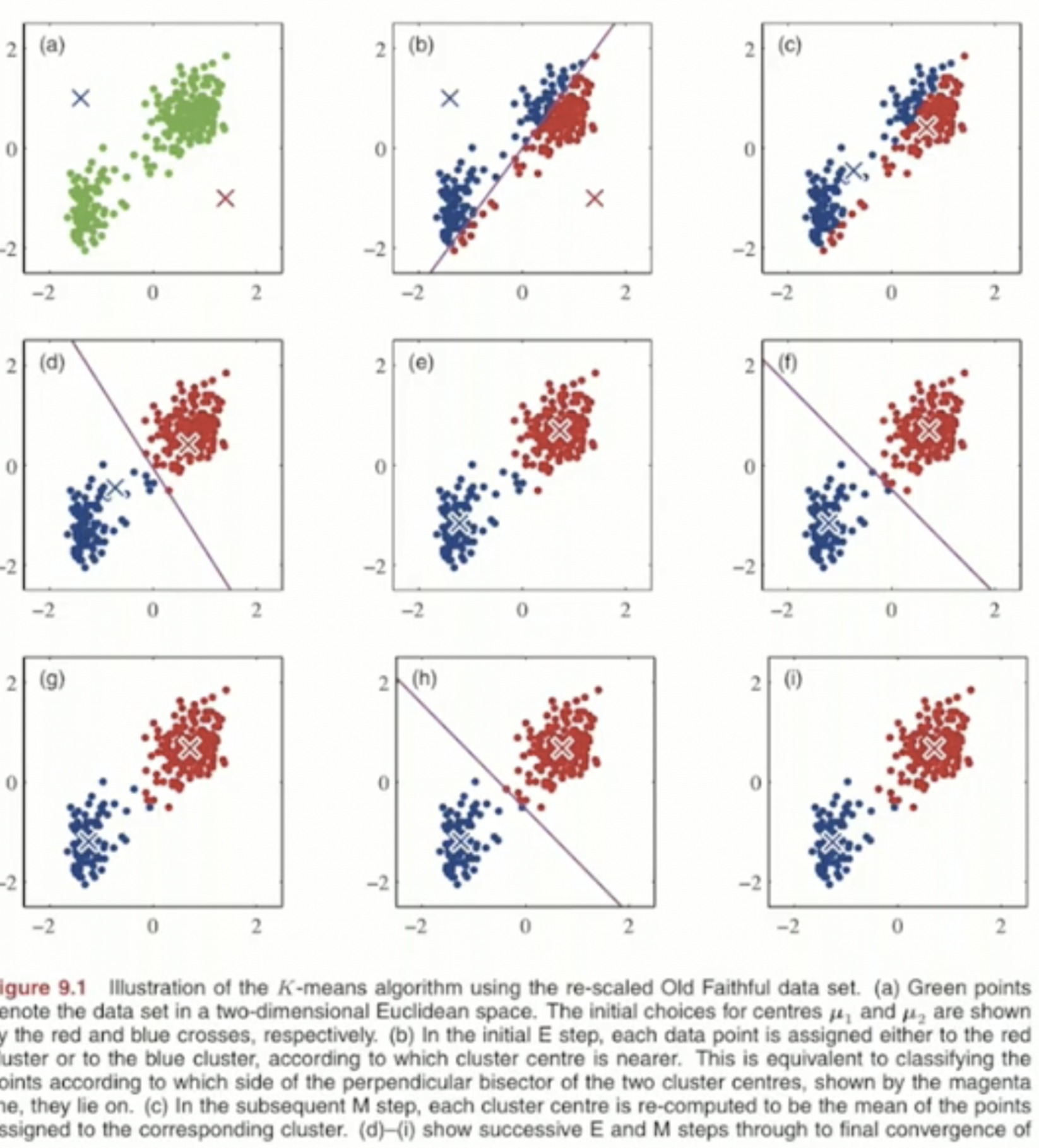
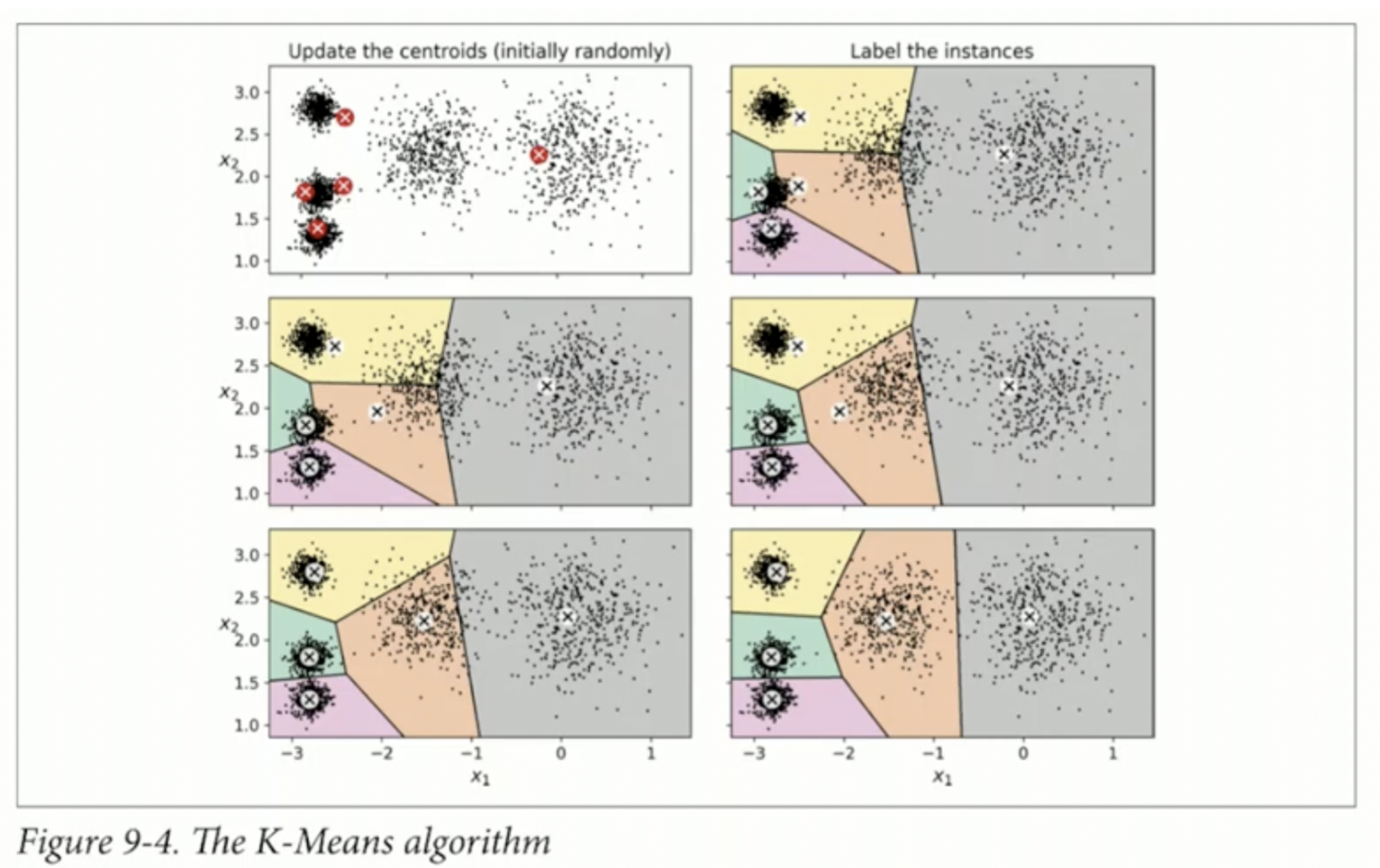
해당 그림이 k-means clustering을 가장 잘 표현한 그림이다.

$k$를 2로 설정하고, $\mu$의 초기 위치를 random하게 설정한다. 주어진 sample과 주어진 centroid의 위치를 비교해서 어떤 $\mu$와 가까운지에 대해 색을 구분하여 군집을 구별했다. 해당 두 점을 수직으로 등분하는 선이 경계값이 된다. 이후 $\mu$를 업데이트 하고, 이를 반복하여 최종 그림인 (i)가 나오게 된다.

K-means: method

input 값은 $\{ x_1, x_2, ..., x_N \}$, $k = 1, ..., K$인 $\mu_k$가 주어진다.

사실 K-means도 최적화 문제인데

위 수식처럼 정의된 cost를 최적화 하는 문제이다.

예를 들어 label $R = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ \end{bmatrix}$을 $\sum_{n=1}^{3}\sum_{k=1}^{2}r_{nk}\|x_n-\mu_k\|^2$를 계산하면 $r_{nk}$ 때문에 결과적으로는 $\|x_1-\mu_1\|^2 + \|x_2-\mu_2\|^2 + \|x_3-\mu_1\|^2$라는 식이 나오게 된다.

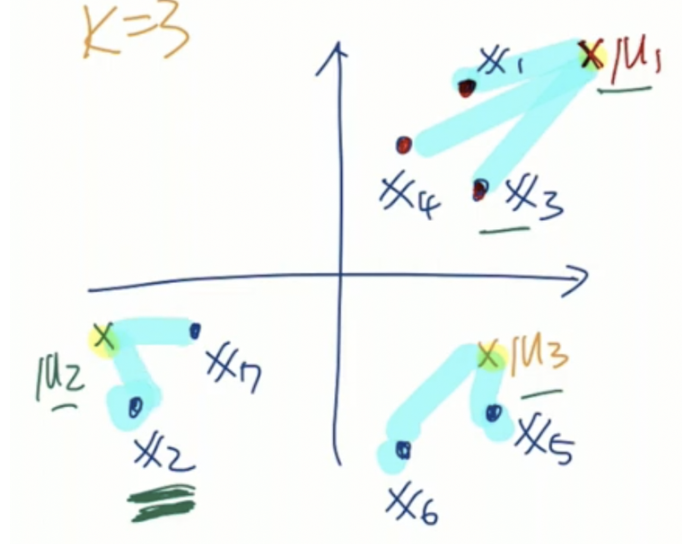
결국 cost $J$는 sample과 해당 sample로 부터 가장 가까이 존재하는 centroid와의 거리의 제곱의 합을 의미한다.

해당 cost를 minimize한다면 centroid가 모여있는 sample 모두와 가장 가까운 거리가 될 때를 의미한다.

위 수식과 같이 표현할 수 있지만 해당 수식은 결론 $R$을 구하겠다는 의미이다.

또한 $\mu$를 업데이트 하는 수식은 다음과 같다

여기서 분모는 $k$번째 속하는 sample의 개수이고, 분자는 $k$번째 속하는 sample의 합이다.

k-means에서는 boundary가 어떻게 나타나는지도 중요하다.

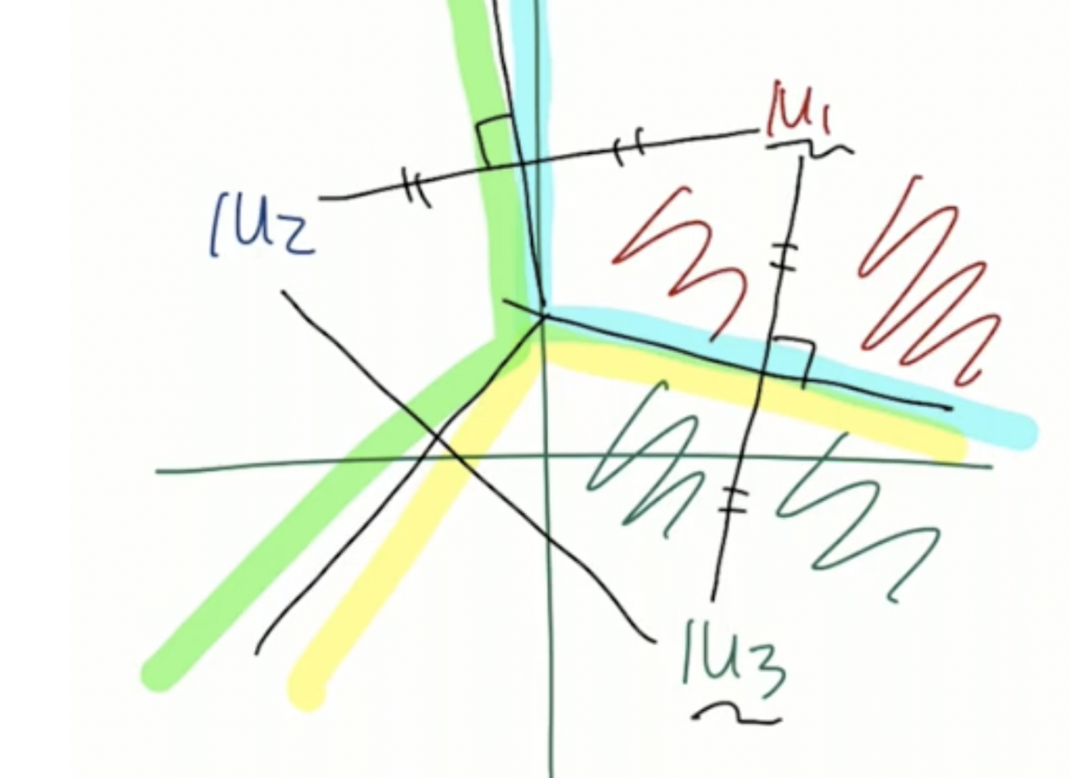
다음과 같이 boundary를 기준으로 sample이 어떤 군집에 위치하는지 정해진다.

해당 decision boundary는 다음과 같은 성질이 있는데 첫 번째는 convex하다는 점이고, 두번째는 single connect라는 것이다. 그리고 우리는 해당 boundary를 Voronoi tessellation이라고 부른다.

single connect라는 점은 각각의 수직 이등분선으로 연결되기 떄문이다.

Mixture of Gaussian Clustering

k-means와의 공통점은 iterative하게 동작한다는 점이다. 그러나 차이점은 k-means는 discrete하여 label이 one-hot으로 표현되어있지만, MoG의 경우 probabilistic 확률적으로 표현된다는 점이다.

즉, 어떤 cluster에 얼마만큼의 확률로 속한다라는 결론이 나오게 된다.

MoG에서는 다음 개념이 중요하다. 첫째, mixture of Gaussian과 둘째, responsibility 마지막으로 parameter을 update하는 방법이다.

Mixture (Mixture distribution)

임의의 distribution은 해당 개형이 어떻게 나올지 모른다.

이러한 임의의 형상의 확률 분포를 다룰 때 mixture distribution 을 사용한다.

즉, 우리가 알고 싶은 무작위한 확률 분포를 우리가 기존에 사용할 수 있는 확률분포의 합으로 표현한다.

$p(x) = \frac{1}{3}p_1(x)+\frac{1}{3}p_2(x)+\frac{1}{3}p_3(x) = \sum_{k=1}^{K}\pi_kp_k(x)$로 표현하고, $\pi$를 mixing coefficient라고 표현한다. mixing coefficient가 가져야 할 조건은 하나인데 $\sum \pi_k = 1$을 만족해야한다. 이는 확률 분포 함수는 모든 범위에서 합하면 1이 되어야 하기 때문에, 각 독립적인 분포의 합을 1로 만들기 위함이다. 해당 정도는 모두 달라도 괜찮으며 합하여 1만 나오면 된다.

Mixture of Gaussian

이는 gaussian distribution을 섞어서 만든 mixture distribution을 나타낸다.

해당 모델은 parameter로 $\pi, \mu, \sigma$ 를 가진다.

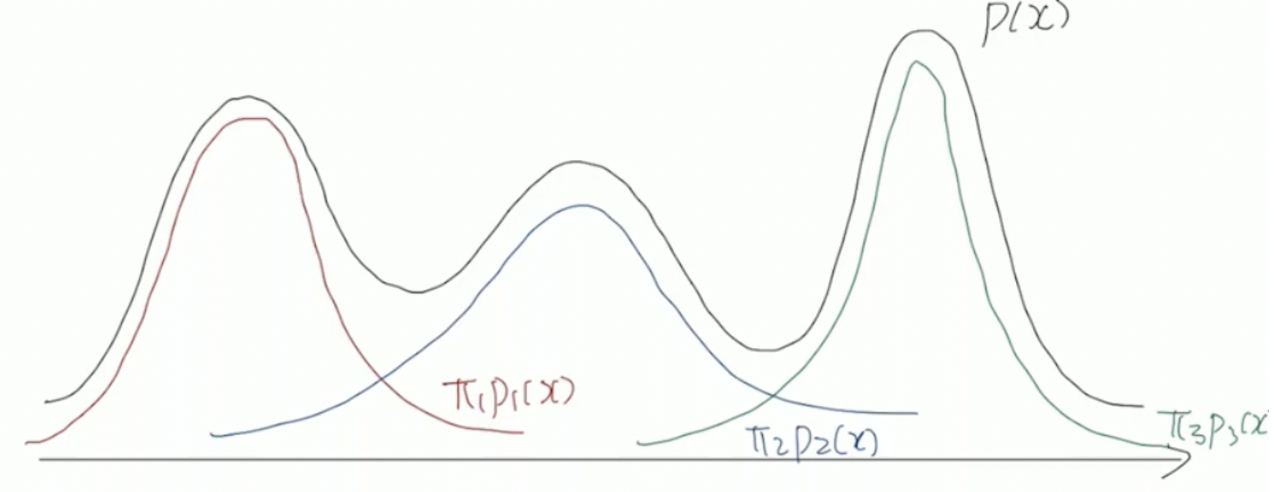
위의 그림과 같은 mixture distribution이 존재한다고 가정하자.

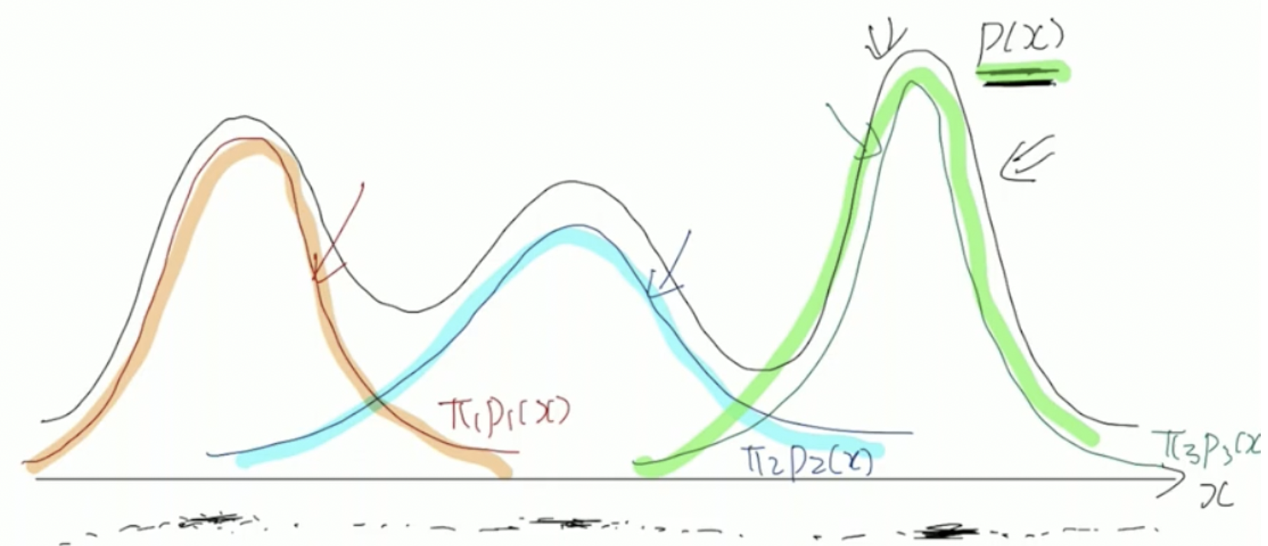
MoG를 통해 clustering을 진행하는 경우 다음과 같은 형태로 군집이 형성된다.

Responsibility

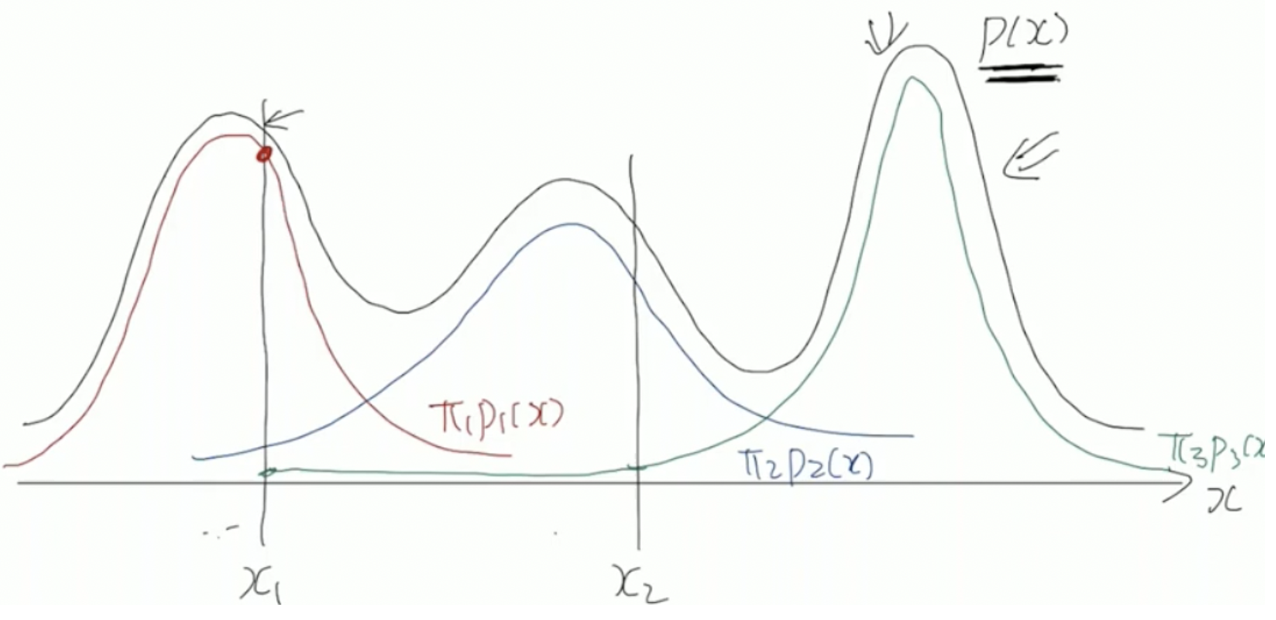
임의의 점 $x_1$에 대해서 $p(x_1) = \pi_1p_1(x_1) + \pi_2p_2(x_2) + \pi_3p_3(x_3)$으로 구할 수 있다.

responsibility는 $p(x_1)$의 값을 구하는 데, 각 $p_1(x_1), p_2(x_1), p_3(x_1)$이 얼마만큼의 기여를 했는가이다.

이를 $\gamma$로 표현하는데 현재 확률 / 전체 확률 로 구할 수 있으며, 수식으로 나타내면 다음과 같다

$\gamma_1 = \frac{\pi_1p_1(x_1)}{p(x_1)}$, $\gamma_2 = \frac{\pi_2p_2(x_1)}{p(x_1)}$, $\gamma_3 = \frac{\pi_3p_3(x_1)}{p(x_1)}$

또한 $\sum \gamma = 1$이다.

$x_n$ 은 $n$번째 sample을 의미하며, $k$는 $k$번째 distribution을 의미한다.

k-means를 사용했을 때와 MoG를 사용했을 때의 차이점을 비교해보자

$r_{nk} = \begin{bmatrix} 1&0&0\\0&1&0\\0&1&0\\0&0&1\\1&0&0\\ \end{bmatrix}, \space \space \space \space \space \space \space \gamma_{nk} = \begin{bmatrix} 0.8&0.1&0.1\\0.2&0.7&0.1\\0.3&0.6&0.1\\0.1&0.2&0.7\\0.9&0.1&0\\ \end{bmatrix}$

다음과 같이 label이 주어졌을 때, 크게 본다면 k-means의 경우 label이 discrete함을 알 수 있고, MoG의 경우 label이 probabilistic 한 것을 알 수 있다. responsibility를 column에 대한 합을 $N$이라고 표현하고 수식으로 다음과 같이 작성한다. $N_k = \sum_n \gamma_{nk}$. 이는 확률 모델을 사용했기 때문이다.

위의 예시에서 구해본다면 $N_1 = 2.3, N_2 = 1.7, N_3 = 1.0$이 나오게 된다.

Parameter update

mixing coefficient: $\pi_i = \frac{N_i}{N}$

$\mu_i = \frac{1}{N_i} ( \gamma_{i1}x_1 + \gamma_{i2}x_2 + \cdots + \gamma_{in}x_n )$

Summary

1. 평균 $\mu_k$, covariance $\sigma_k^2$, mixing cofficient $\pi_k$를 초기화 한다

2. 주어진 sample과 parameter을 사용하여 responsibility를 업데이트 한다

   $\gamma(z_{nk}) = \frac{\pi_k N(x_n | \mu_k, \sigma_k^2)}{\sum_{j=1}^{K}\pi_j N(x_n|\mu_j, \sigma_j^2)}$

3. 해당 responsibility를 통해서 parameter을 업데이트 한다

1. log likelihood를 계산한다 (cost)

   $log \space p(X|\mu, \sigma^2, \pi) = \sum_{n=1}^{N}log\{ \sum_{k=1}^{K}\pi_k N(x_n | \mu_k, \sigma_k^2) \}$

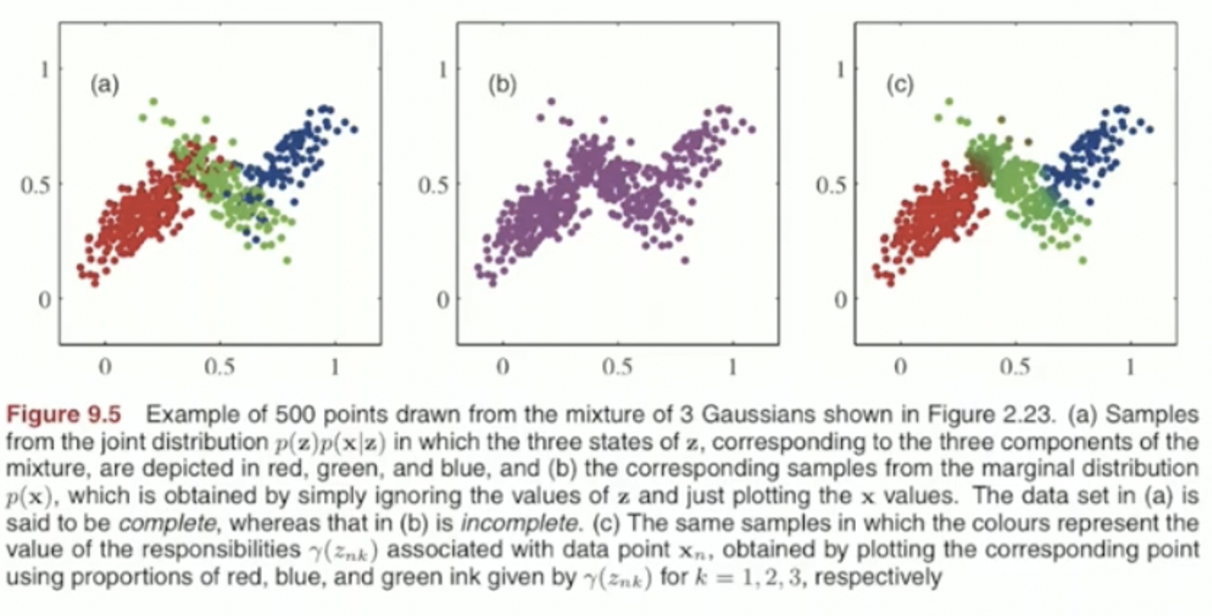
가장 왼쪽의 그림은 label을 discrete 하게 준 것이고, 가장 오른쪽의 그림은 label을 probabilistic하게 표현한 그림이다.

K-means는 주어진 sample $x_n$과 주어진 centroid $\mu_k$를 통해 distance $\|x_n - \mu_k\|_2$를 통해 label $r_nk$ 를 구하고 $\mu_k$를 업데이트 하며 iterative 하게 동작한다

MoG의 경우 주어진 sample $x_n$ 과 주어진 parameter $\pi_k, \mu_k, \sigma_k^2$ 를 통해 responsibility $\gamma_{nk}$를 구하고, 이를 통해 parameter을 업데이트 하여 iterative 하게 동작한다.

지금까지 $\sigma_k^2$로 표현했지만 $\Sigma_k$로 표현해도 같은 표현이다.