Linear Regression
Linear regression → 연속적인 값을 추정
Normal equation → 선형대수학적으로 최적화된 해를 구함
Gradient descent → 값의 근사 (미분을 이용)
What is Linear Regression
input → model → output
(trainset) (prediction)
이때, cost를 최소화 하는 방향으로 학습을 시킴 → model에 대한 개선
Linear model
input (vector) → linear model (linear regression) → output (real number, scalar)
y^=θ0+θ1x1+θ2x2+...+θnxn=ΘTx
-
y^은 실제 y에 대한 예측된 변수
-
n은 feature의 수, n차원, input에 들어있는 값의 수
-
xi의 경우 i번째 feature 값
-
θj의 경우 j번째 model parameter, 각 feature에 대한 weight θ1,θ2,...,θn에 bias인 θ0을 더한 값
-
Θ는 model의 parameter vector을 나타냄. model을 기술하는데 필요한 parameter
-
x의 경우 feature vector이다. 이는 input이다. x0의 경우 1이며, 이는 bias를 위한 값이다.
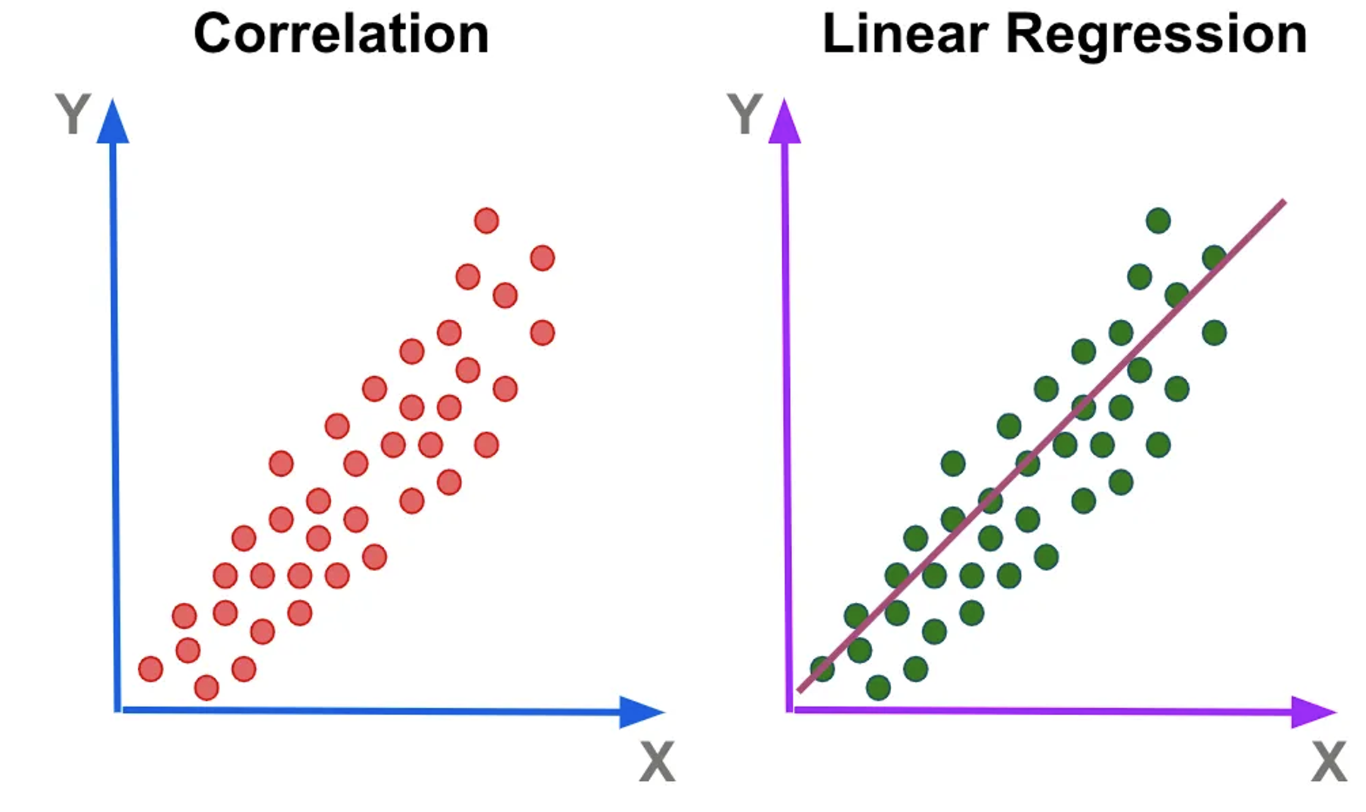
y^=θ0+θ1x1
- θ=[01]
- θ=[−12]
이 때, bias θ에 따라 직선의 기울기가 달라진다. parameter θ0과 θ1을 조정하여 주어진 data를 가장 잘 설명하는 parameter θ를 구한다.
parameter θ가 결정되는 순간 예측값은 하나의 직선으로 표현된다 → 우리의 prediction을 모든 영역에 대해 표현한다
실제값과 예측값의 차이를 error라고 할 때, error = y−y^로 표현할 수 있다.
이때, error의 값은 거리값이므로 (y−y^)2로 제곱을 취하고, 이는 항상 양수값이다.
i ierror(i)=(y(i)−y^(i))2로 표현할 수 있고, 각 sample에 대한 error을 정의할 수 있다.
∑i=15error(i)2=∑i=15(y(i)−y^(i))2을 위의 1번 model과 2번 model에 대해 구할 수 있다.
1번 model의 error2의 값을 20, 2번 model의 error2의 값을 100이라 할 때, 주어진 data를 잘 설명하는 model은 1번 model이라고 할 수 있다.
Cost function
linear regression model에 대한 parameter은 어떻게 찾는가?
model을 training한다는 뜻은 적합한 주어진 training set에 가장 적합한 model을 찾아냄을 의미한다.
가장 먼저 현재 주어진 데이터에 대해 model이 얼마나 fit한지 판단해야 한다
regression problem에 사용되는 measure, error index, cost function은 다음과 같다
θ^=arg min RMSE(X,Θ)=arg min m1i=1∑m(y(i)−ΘTx(i))2=arg min MSE(X,Θ)=arg min m1i=1∑m(y(i)−ΘTx(i))2=arg min SSE(X,Θ)=arg mini=1∑m(y(i)−ΘTx(i))2
여기서 ΘTx(i)=y^(i)이다.
RMSE: Root Mean Of Squared error
MSE: Mean Of Squared error
SSE: Sum Of Squared error
RMSE, MSE, SSE를 최소로 만드는 argument의 해는 동일하다
Design matrix
- regressor matrix, model matrix, data matrix
- model은 y^=ΘTx
- training dataset은 (x(1),y(1)), (x(2),y(2)), (x(3), y(3)), ..., (x(m),y(m))
- model prediction은 (y^(1)=ΘTx(1)), (y^(2)=ΘTx(2)), (y^(3)=ΘTx(3)), ... , (y^(m)=ΘTx(m)),
- SSE는 (y(1)−ΘTx(1))2+(y(2)−ΘTx(2))2+(y(3)−ΘTx(3))2+...+(y(m)−ΘTx(m))2
이를 input X=⎣⎢⎢⎢⎢⎡x(1)Tx(2)T⋮x(m)T⎦⎥⎥⎥⎥⎤일 때, y^=⎣⎢⎢⎢⎢⎡y^(1)y^(2)⋮y^(m)⎦⎥⎥⎥⎥⎤ = X⋅Θ=⎣⎢⎢⎢⎢⎡x(1)Tx(2)T⋮x(m)T⎦⎥⎥⎥⎥⎤⋅Θ로 표현할 수 있다.
SSE(Θ)=∑i=1m(y(i)−ΘTx(i))2=∥y−y^∥22=∥⎣⎢⎢⎢⎢⎡y(1)y(2)⋮y(m)⎦⎥⎥⎥⎥⎤−⎣⎢⎢⎢⎢⎡y^(1)y^(2)⋮y^(m)⎦⎥⎥⎥⎥⎤∥22=∥⎣⎢⎢⎢⎢⎡y(1)−y^(1)y(2)−y^(2)⋮y(m)−y^(m)⎦⎥⎥⎥⎥⎤∥22
Design matrix에 대해 training dataset이 m개, feature vector x의 차원이 n일 때, m개의 sample을 row vector로 한 design matrix X로 표현할 수 있다.
Normal Equation
Geometric approach
Design matrix X의 각 열을 xj라고 하면
y^=XΘ=⎣⎢⎢⎢⎡1x1...xn⎦⎥⎥⎥⎤⋅⎣⎢⎢⎢⎡θ0θ1,...θn⎦⎥⎥⎥⎤=θ01+θ1x1+θ2x2+...+θnxn
즉, y^는 x1,x2,...,xn이 생성하는 hyperplane인 span{1,x1,...,xn} 상에 존재한다
Residual(잔차) 또는 error의 크기 ∥y−y^∥을 최소화 하기 위해서는 위의 hyperplane과 errory−y^가 서로 수직이어야 한다
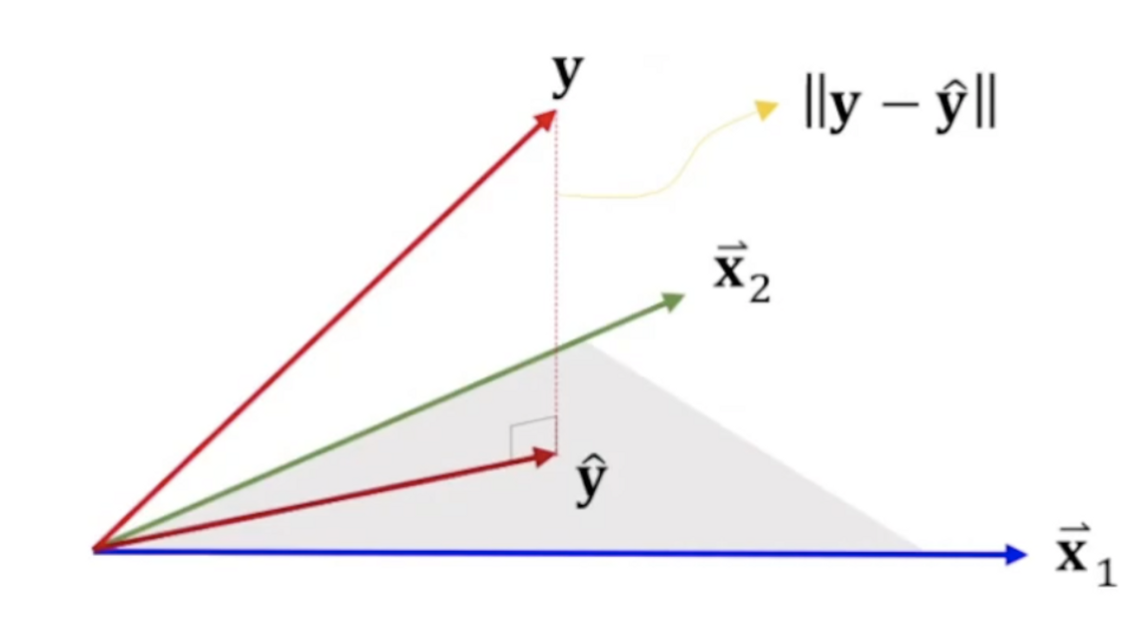
y^=X⋅Θ∈span{x1,x2,...,xn}
y^는 span이라는 평면 위에 존재해야 한다. 이 때, y와 y^과의 거리가 가장 짧은 parameter θ를 찾는다
이는 target인 y와 prediction인 y^가 수직에 위치할 때 거리가 가장 짧다
즉, min ∥y−y^∥⇔(y−y^)⊥span{x1,x2,...,xn}이다.
즉, 모든 column vector에 대해서 xjT⋅(y−y^)=0이 성립해야 한다. → (수직이므로 내적값은 0)
전체 m의 sample에 대해 XT⋅(y−Xθ)=0⇒XTXθ=XTy이고, θ^=(XTX)−1XTy이다
이는 θ^=(XTX)−1XTy⇔θ^=arg min SSE(θ)를 유도한 것이다.
Analytic approach
Sum of squared error (SSE)에 대해
SSE=i=1∑m(y(i)−y^(i))2=∥y−y^∥2=(y−y^)T(y−y^)
y^=Xθ를 사용하여
SSE(θ)=yTy−2yTXθ+(Xθ)T(Xθ)=yTy−2yTXθ+θTXTXθ
∂θ∂SSE(θ)=2(XTXθ−Xy)=0⇒XTXθ=XTy
위 SSE를 미분하여 0이 나오는 값을 찾는다
따라서 우리는
θ^=(XTX)−1XTy
y^=X(XTX)−1XTy
라는 normal equation을 얻을 수 있다.
Computational complexity
Normal equation의 계산
- Normal equation에 의한 예측치 y^=X(XTX)−1XTy
- X∈Rm×n
- XTX∈Rn×n
- (XTX)−1의 계산 복잡도 = O(n2.4) ~ O(n3)
- Feature 수의 약 세제곱으로 계산 시간이 증가한다



