Rasterization(래스터화)

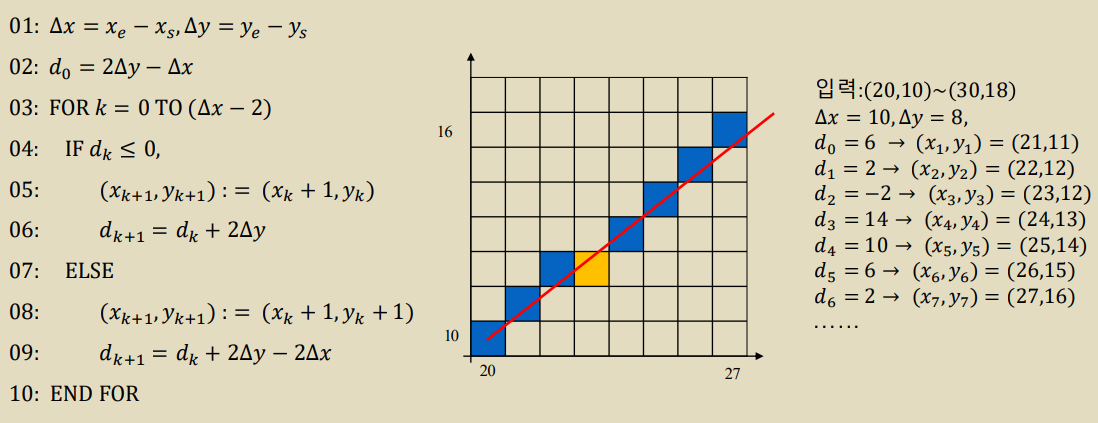
1. Rasterization이란?

• 지난 시간에 배운 기본 객체를 정수 좌표를 갖는 스크린(칼라 버퍼, 프레임 버퍼)에 그리는 과정이다.
  ✔기본 객체 위의 모든 점은 정수 좌표를 갖는 가까운 픽셀의 좌표로 반올림 되어야 한다.
• 3차원 장면은 다양하고 많은 수의 그래픽스 출력 객체를 포함하기에 각각의 출력 객체에 대한 빠르고 효율적인 래스터화 기법을 필수로 이용한다.

⚫ 양 끝점이 주어진 라인의 래스터화

• Bresenham(Midpoint) Algorithm 이라고 한다.

2. Bresenham(Midpoint) Algorithm

• 시작점 (𝑥𝑠, 𝑦𝑠) 과 끝점 (𝑥𝑒, 𝑦𝑒) → Δ𝑥 = 𝑥𝑒 − 𝑥𝑠, Δ𝑦 = 𝑦𝑒 − 𝑦s

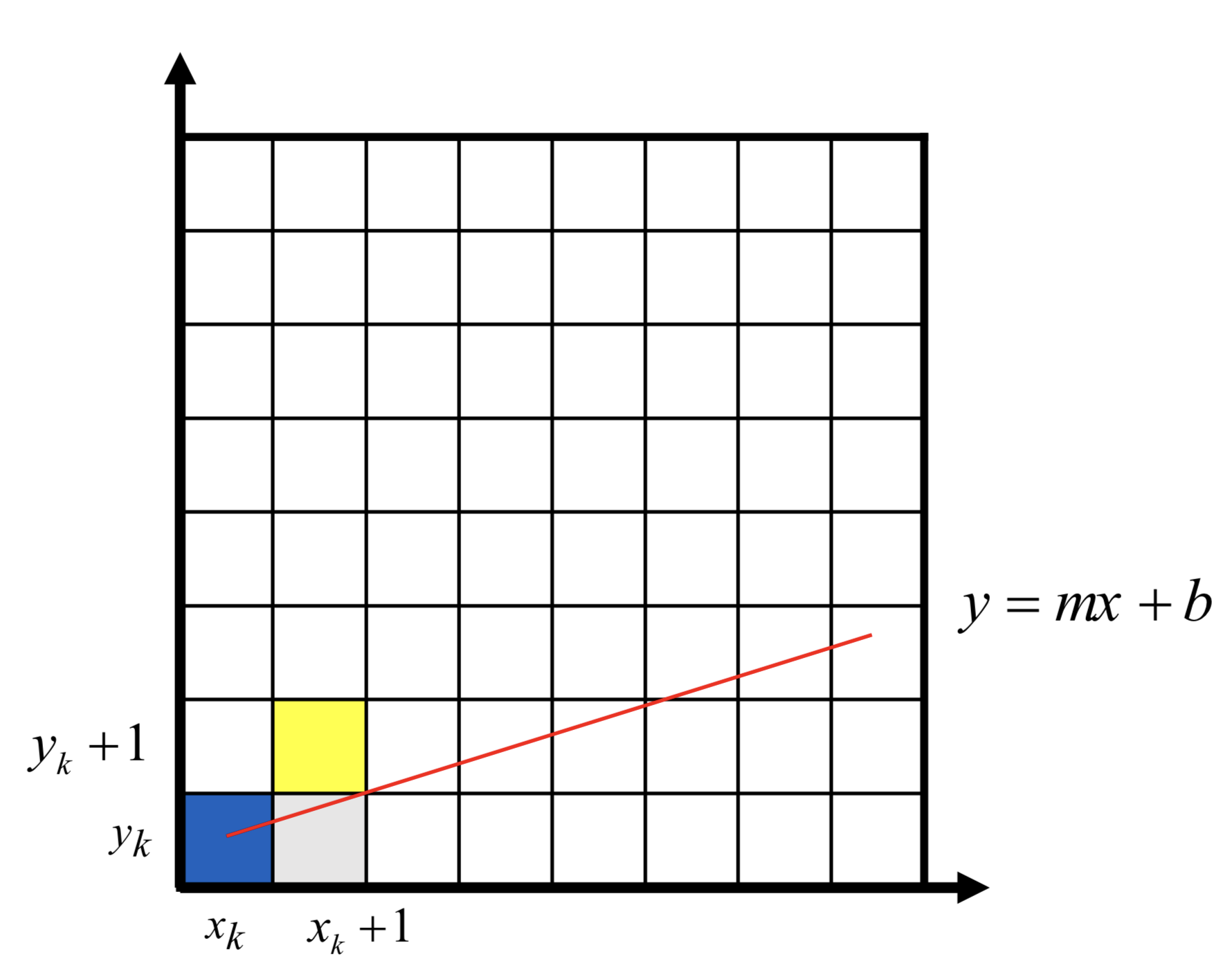
• 기울기 0 ≤ 𝑚 (=Δ𝑦/Δ𝑥)≤ 1을 가정하고, 𝑥좌표를 1씩 증가

• 현재 위치: (𝑥𝑘, 𝑦𝑘)

• 다음 위치: (𝑥𝑘 + 1, 𝑦𝑘) 또는 (𝑥𝑘 + 1, 𝑦𝑘 + 1)
  

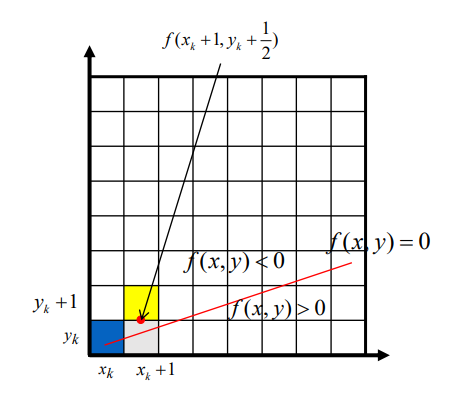
• 직선의 음함수(Implicit) 표현

  직선 𝑦 = 𝑚𝑥 + 𝑏 의 음함수 표현, 𝑓 (𝑥, 𝑦) = 𝑚𝑥 − 𝑦 + 𝑏, 여기서 𝑚 =Δ𝑦/Δ𝑥

• 𝑓 (𝑥, 𝑦) > 0: 점 𝑥, 𝑦 는 직선 아래 존재

• 𝑓 (𝑥, 𝑦) = 0: 점 𝑥, 𝑦 는 직선 상에 존재

• 𝑓 (𝑥, 𝑦) < 0: 점 𝑥, 𝑦 는 직선 위에 존재

• 중간점의 부호 조사

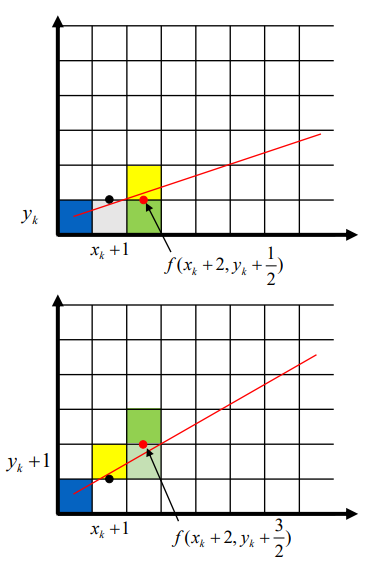
  • 𝑓 (𝑥𝑘 + 1, 𝑦𝑘 + 0.5) ≤ 0 -> (𝑥𝑘 + 1, 𝑦𝑘) 선택
  • 𝑓 (𝑥𝑘 + 1, 𝑦𝑘 + 0.5) > 0 -> (𝑥𝑘 + 1, 𝑦𝑘 + 1) 선택
  

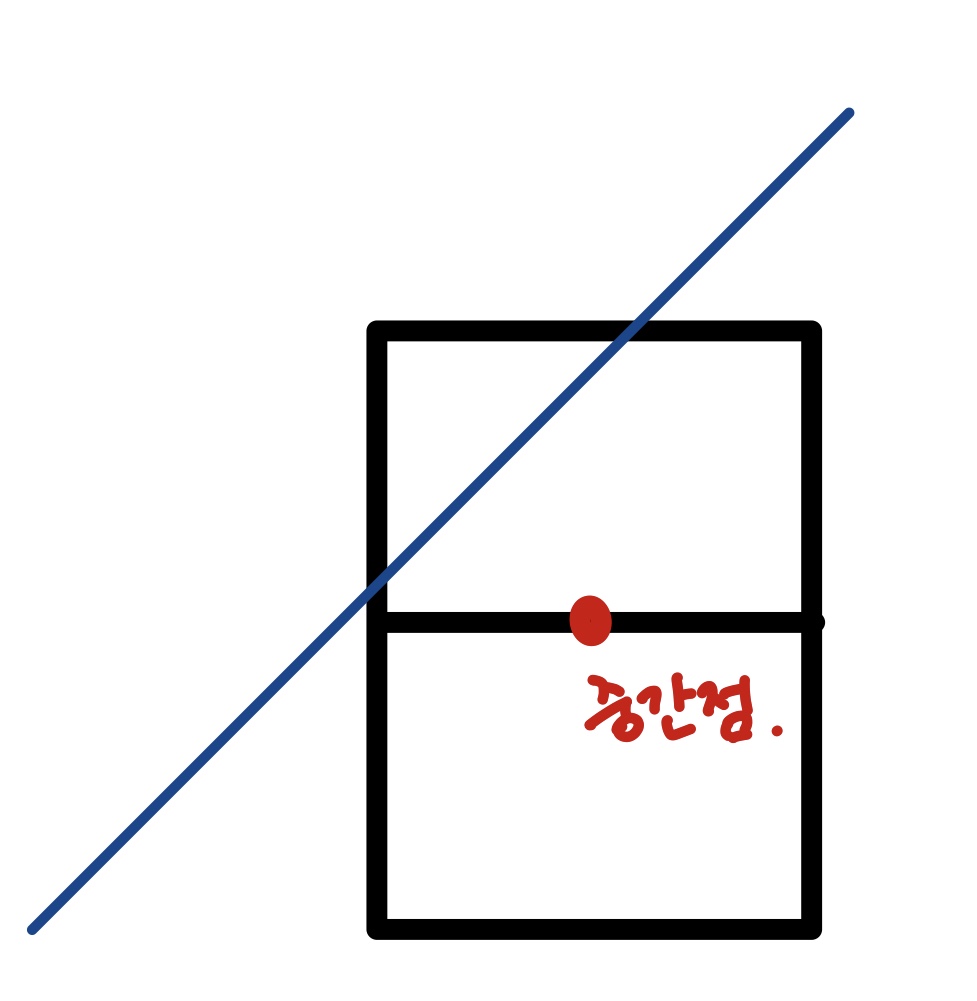
• 𝑓 (𝑥𝑘 + 1, 𝑦𝑘 + 0.5) ≤ 0 라면 중간점이 직선의 위에 있는 것이므로 (𝑥𝑘 + 1, 𝑦𝑘)인 회색을 고를 것이다. 따라서 y의 위치는 변하지 않는다. (❗ 위의 그림 참고)
• 𝑓 (𝑥𝑘 + 1, 𝑦𝑘 + 0.5) > 0 라면 중간점이 직선의 아래에 있는 것이므로 (𝑥𝑘 + 1, 𝑦𝑘 + 1)인 노란색을 고를 것이다. 따라서 x와 y의 위치가 둘 다 변한다. (❗ 아래 그림 참고)

3. Bresenham(Midpoint) Algorithm 판별식

판별식

• 초기 판별식 𝑑0 = ?

𝑓 𝑥, 𝑦 = Δ𝑦/Δ𝑥 * 𝑥 − 𝑦 + 𝑏

𝑑0 = 2Δ𝑥𝑓(𝑥0 + 1, 𝑦0 + 0.5)
= 2Δ𝑥{Δ𝑦/Δ𝑥 (𝑥0 + 1) − (𝑦0 + 0.5) + 𝑏}
= 2Δ𝑥{Δ𝑦Δ𝑥 * 𝑥0 − 𝑦0 + 𝑏 +Δ𝑦/Δ𝑥 − 0.5
= 2Δ𝑦 − Δ𝑥

증분적 판별식

• 𝑑𝑘로 부터 𝑑𝑘+1을 계산할 수 없을까?

  • 𝑑𝑘 = 2Δ𝑦(𝑥𝑘 + 1) − 2Δ𝑥𝑦𝑘 − Δ𝑥 + 2Δ𝑥�

Case 1: 𝑑𝑘 ≤ 0
𝑑𝑘+1 = 2Δ𝑥𝑓 𝑥𝑘 + 2, 𝑦𝑘 + 0.5
= 2Δ𝑥{Δ𝑦/Δ𝑥 (𝑥𝑘 + 2) − (𝑦𝑘 + 0.5) + 𝑏}
= 2Δ𝑦 (𝑥𝑘 + 1) − 2Δ𝑥𝑦𝑘 − Δ𝑥 + 2Δ𝑥𝑏 + 2Δ𝑦
= 𝑑𝑘 + 2Δ𝑦

Case 2: 𝑑𝑘 > 0
𝑑𝑘+1 = 2Δ𝑥𝑓 𝑥𝑘 + 2, 𝑦𝑘 + 1.5
= 2Δ𝑥{Δ𝑦/Δ𝑥 (𝑥𝑘 + 2) − (𝑦𝑘 + 1.5) + 𝑏}
= 2Δ𝑦 (𝑥𝑘 + 1) − 2Δ𝑥𝑦𝑘 − Δ𝑥 + 2Δ𝑥𝑏 + 2Δ𝑦 − 2Δ𝑥
= 𝑑𝑘 + 2Δ𝑦 − 2Δ𝑥

Bresenham Algorithm

• 입력: 시작점(𝑥𝑠, 𝑦𝑠) 끝점(𝑥𝑒, 𝑦𝑒) (0 < 𝑚 < 1)