[논문 리뷰] NeRV: Neural Representations for Videos

Motivation

• NeRF와 같이 video를 time에 대한 함수로 나타낼 수 있지 않을까? (Implicit neural representation)
  • $v_t = f_\theta(t)$
    • $v_t$ : video frames
    • $f_\theta$ : neural network
• 이를 통해, video를 neural network $f_\theta$로 나타내면, video를 model로 표현할 수 있다.
  • video compression task를 model compression task로 치환 가능

Contribution

• video에 대한 새로운 image-wise implicit representation을 제안
• video compression problem을 model compression problem으로 치환
  • standard model compression tool로 conventional compression method와 비슷한 성능을 보임
• Video denoising task에서도 적용 가능 (특별한 denoising design없이)

Method

NeRV Architecture

NeRV의 목적은 frame index $t$가 input으로 주어졌을 때, function $f_\theta$를 통해 video에서 $t$에 해당하는 RGB video frame $v_t$를 output으로 출력하는 것이다:

• $f_\theta : \mathbb{R} \rightarrow \mathbb{R}^{H \times W \times 3}$, $v_t \in \mathbb{R}^{H \times W \times 3}$
• $v_t = f_\theta(t)$

이때, frame index $t$를 그대로 넣는 것은 좋은 결과를 주지 못했고, 이를 Positional Encoding을 통해 high embedding space로 mapping하여 넣는 방법을 택한다.

여기서 $b$와 $l$은 hyper-parameter이고, $t$는 $[0,1)$로 normalize 되어 들어간다.

Network Architecture

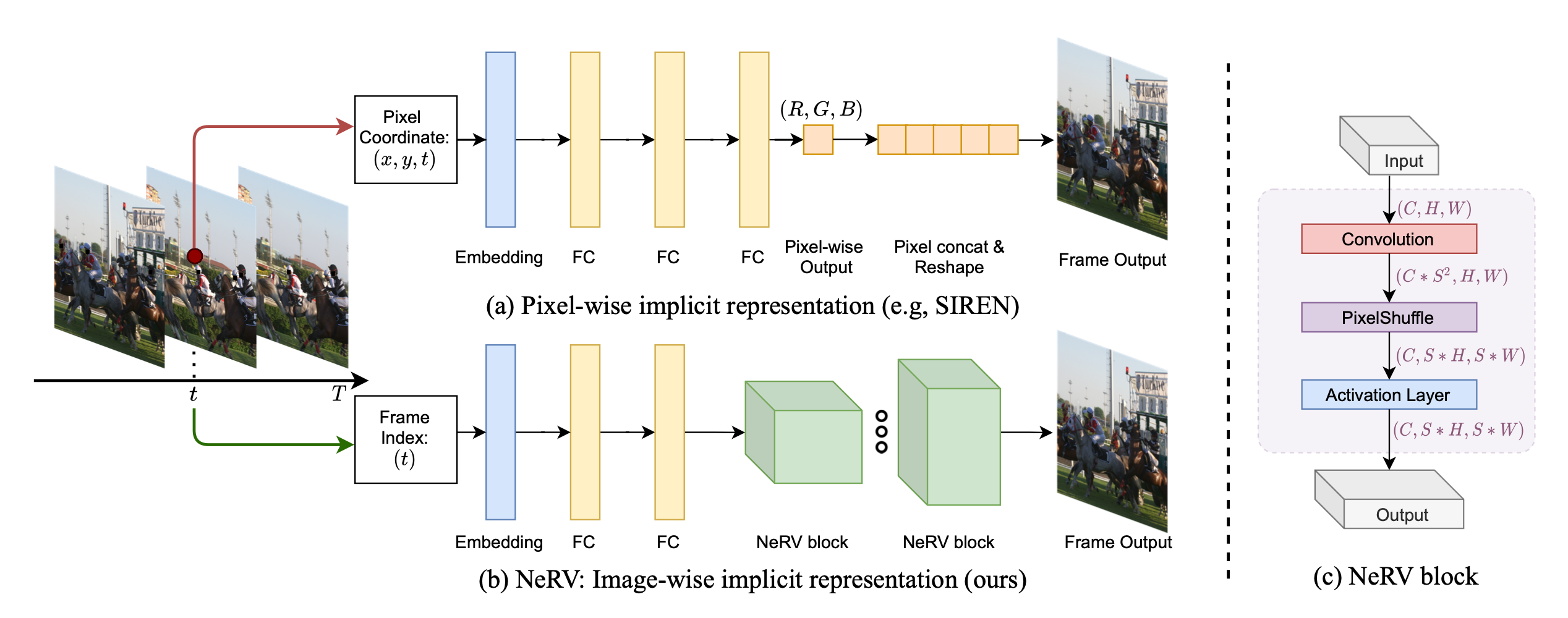
(a)의 경우는 기존의 pixel-wise implicit representation network이며, (b)는 논문에서 제시한 NeRV의 image-wise implicit representation을 위한 network이다.

MLP를 통해 모든 픽셀 값을 출력하는 것은 너무 많은 파라미터를 요구하므로, 그림에서 보이는 것과 같이, convolution kernel를 공유하는 convolution을 사용하여, efficient network를 설계하였다.

Loss objective

loss 함수는 위와 같이, L1 loss와 SSIM loss를 사용하였다.

Model Compression

논문에서는, model compression을 위해 순차적으로 4가지 step을 거친다:

1. video overfit
   • 하나의 video에 최적화 함으로써, 모델의 크기를 경량화
2. model pruning
   • standard pruning 기법과 동일하게 weight threshold 이하의 weight는 0으로 변경
     $\theta_i =\begin{cases} \theta_i, & \text{if } \theta_i \geq \theta_q \\0, & \text{otherwise},\end{cases}$
3. weight quantization
   • post-hoc quantization (after training process)
     $\mu_i = \text{round} \left( \frac{\mu_i - \mu_{\text{min}}}{2^{\text{bit}}} \right) \cdot \text{scale} + \mu_{\text{min}}, \quad\text{scale} = \frac{\mu_{\text{max}} - \mu_{\text{min}}}{2^{\text{bit}}}$
4. weight encoding
   • Huffman Coding 사용