[시계열] 02. RNN의 문제점과 LSTM의 등장

😍 먼저, 시계열에 대한 블로그 내용은 밑바닥부터 시작하는 딥러닝 2 도서를 기반으로 작성되었음을 밝힙니다.

---

RNN의 문제점

RNN은 아래 두 가지 원인으로 시계열 데이터의 장기 의존 관계를 학습하기 어렵다는 문제점이 존재한다.

• 기울기 소실
• 기울기 폭발

• 특정 문장에서 언어 모델을 학습하는 과정

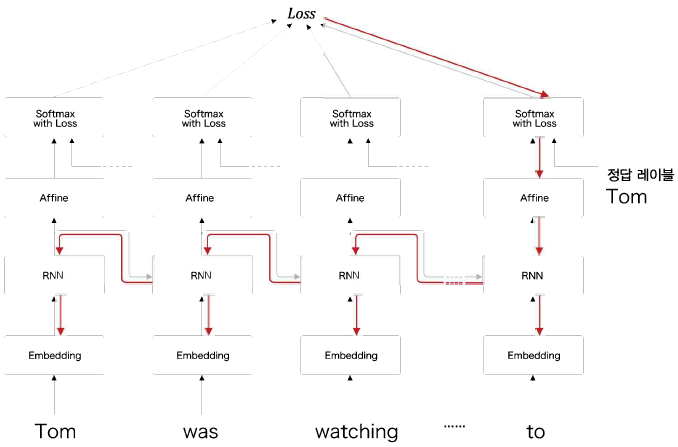
정답 레이블이 "Tom"이라고 주어진 시점으로부터 과거 방향으로 기울기를 전달하며,
과거 방향으로 계속해서 '의미 있는 기울기'를 전달하여 시간 방향의 의존 관계를 학습한다.

하지만, RNN 계층에서는 시간을 거슬러 올라갈수록 기울기가 소실되거나 폭발하여 장기 의존 관계를 학습할 수 없게 된다.

기울기 소실 및 폭발의 원인

한 개의 RNN 계층에서는 $h_t = \tanh(h_{t-1}W_h + x_tW_x+b)$의 계산 과정을 수행하고,
따라서, 역전파로 전해지는 기울기는 $\tanh, +, MatMul$ 연산을 차례로 통과한다.

이 때, +는 상류의 기울기를 그대로 하류로 흘려보내지만,
$\tanh, MatMul$ 두 연산에서는 기울기가 변화하게 된다.

1) $\tanh$의 기울기 변환

$(\tanh(x))' = 1-x^2$

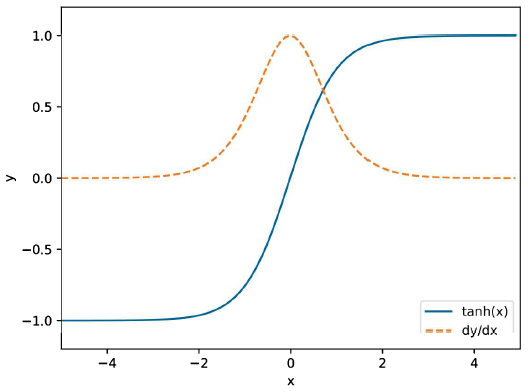
$(\tanh(x))$의 기울기는 x = 0으로부터 멀어질수록 1부터 0까지 계속 작아지며,
이는 역전파에서 기울기가 $\tanh$ 노드를 지날 때마다 값이 계속 작아짐을 의미한다 : 기울기 소실

2) $MatMul$의 기울기 변환

$MatMul$ 노드의 역전파는 매번 같은 가중치 $W_h$가 사용된다.
$W_h$를 T번 반복하여 곱하기 때문에, $W_h$이 1보다 크면 지수적으로 증가하고, 1보다 작으면 지수적으로 감소한다.

• $W_h$ > 1 : 기울기 폭발
• $W_h$ < 1 : 기울기 소실

이 때, $W_h$가 행렬이라면, 행렬의 특잇값 중 최대값이 척도가 되어 1과 비교하여 기울기 변화를 예측할 수 있다.

기울기 폭발 대책

기울기 클리핑

기울기의 L2 norm (g)가 특정 임계값 이상이 되면, 기울기에 (임계값/g)를 곱하여 기울기 폭발을 방지한다.

• 기울기 클리핑 구현

def clip_grads(grads, max_norm):
    total_norm = 0
  	for grad in grads:
  		total_norm += np.sum(grad ** 2)
  	total_norm = np.sqrt(total_norm)
    
    rate = max_norm / (total_norm + 1e-6)
    if rate < 1:
    	for grad in grads:
                grad *= rate            

---

LSTM

RNN의 기울기 소실을 방지하고자 LSTM 모델이 등장한다.

LSTM의 인터페이스

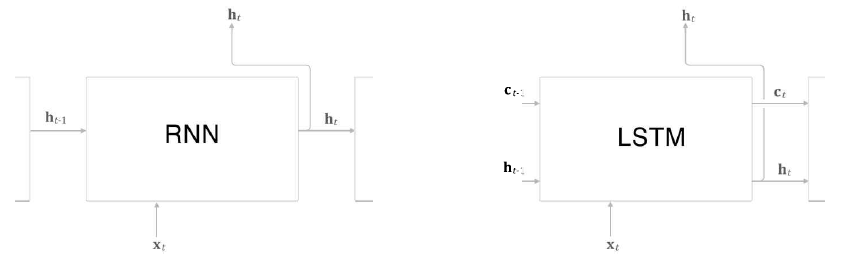
RNN 계층과 달리, LSTM 계층의 인터페이스에는 c라는 기억 셀이 존재한다.

기억 셀은 데이터를 LSTM 계층 내에서만 주고받는다.
즉, LSTM 계층 내에서만 완결되고, 다른 계층으로는 출력하지 않는다.

t에서의 기억 셀 $c_t$에는 과거로부터 시각 t까지의 모든 정보가 저장되어 있으며,
모든 정보를 저장한 기억을 바탕으로 외부 계층에 은닉 상태 $h_t$를 출력한다.

$c_t$는 3개의 입력($c_{t-1}, h_{t-1}, x_t$)으로부터 구할 수 있고,
계산 과정에서 게이트라는 개념이 포함된다.

---

게이트

데이터의 흐름을 제어한다.

• 물의 흐름을 제어하는 게이트로 비유 가능
  

게이트의 열림 상태는 0과 1 사이의 실수로 나타내며, 게이트를 얼마나 열지는 데이터로부터 자동으로 학습한다.

LSTM 계층에는 총 3개의 게이트가 존재한다.

1. output 게이트
2. forget 게이트 + 새로운 기억 셀
3. input 게이트

1. output 게이트

다음 은닉 상태 $h_t$의 출력을 담당하는 게이트

• output 게이트가 추가된 LSTM 계층
  
  

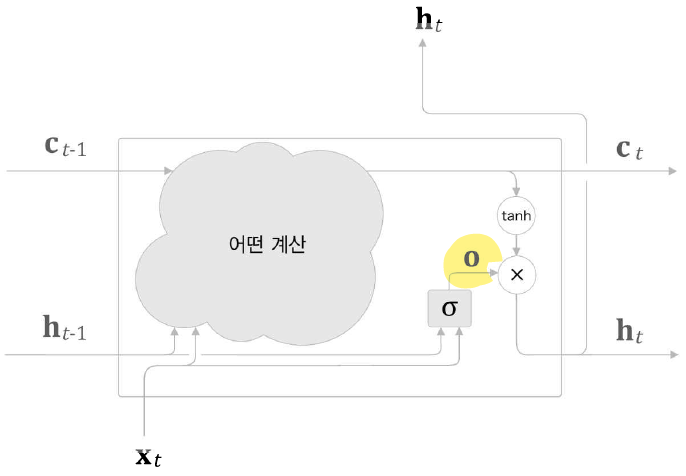
게이트의 열림 상태는 입력 $x_t$와 이전 상태 $h_{t-1}$로부터 구할 수 있으며, 수식은 다음과 같다.

• $W_x, W_h$ : 가중치 매개변수
• $b$ : 편향
• $\sigma$ : 시그모이드 함수

최종적으로, output 게이트의 출력 $o$와 $\tanh(c_t)$의 원소별 곱을 통해 LSTM 계층의 출력 $h_t$를 계산할 수 있다.

2-1. forget 게이트

기억 셀에서 불필요한 기억을 잊게 해주는 게이트

• forget 게이트가 추가된 LSTM 계층
  

  $f = \sigma(x_tW_x^{(f)}+h_{t-1}W_h^{(f)}+b^{(f)})$

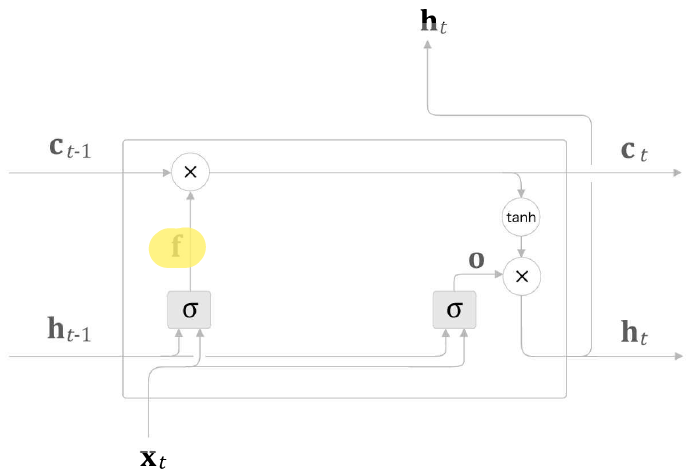
forget 게이트의 출력 $f$와 이전 기억 셀인 $c_{t-1}$의 원소별 곱을 통해 $c_t$를 계산할 수 있다.

2-2. 새로운 기억 셀

기억 셀에 새로 기억해야 하는 정보 추가

• 기억 셀에 필요한 정보가 추가된 LSTM 계층
  
  $g = \tanh(x_tW_x^{(g)}+h_{t-1}W_h^{(g)}+b^{(g)})$

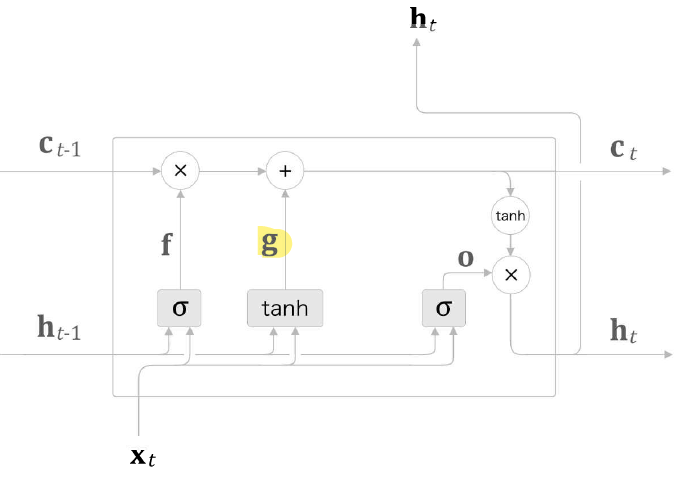
기억 셀에 추가하는 새로운 기억을 g로 표기하며, g가 이전 시각의 기억 셀 $c_{t-1}$에 더해진다.

3. input 게이트

g의 각 원소가 새로 추가되는 정보로써의 가치가 얼마나 큰지 판단하는 게이트

• input 게이트가 추가된 LSTM 계층
  

  $i = \sigma(x_tW_x^{(i)}+h_{t-1}W_h^{(i)}+b^{(i)})$

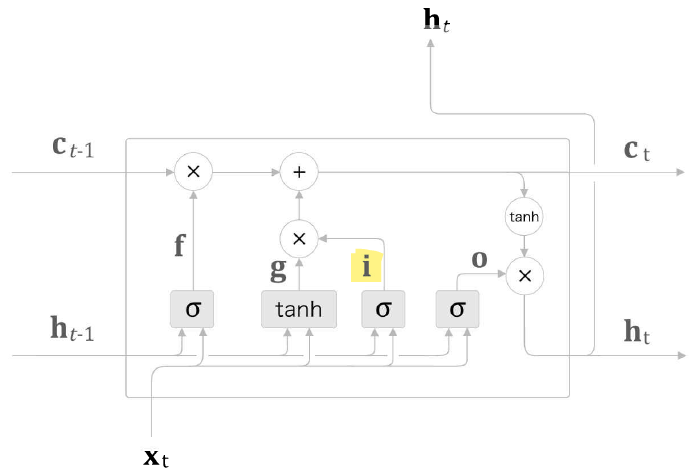
i와 g의 원소별 곱 결과를 기억 셀에 추가한다.

---

LSTM의 기울기 흐름

• 기울기 소실 대책

RNN의 역전파에서는 매번 같은 가중치 행렬을 사용해 행렬 곱을 반복했으므로, 기울기 소실 문제가 발생했다.

반면, LSTM의 역전파에서는 '행렬 곱'이 아닌 원소별 곱이 이루어지고, 매 시각 다른 게이트 값을 이용해 원소별 곱을 계산한다.
매번 새로운 게이트 값을 이용하므로 곱셈 효과가 누적되지 않아 기울기 소실이 일어나지 않는다.

forget 게이트가 '잊어야 한다'고 판단한 원소에 대해서는 기울기가 작아지며,
'잊어서는 안된다'고 판단한 원소에 대해서는 기울기가 약화되지 않은 채로 과거로 전달된다.
따라서, 오래 기억해야 하는 정보의 경우, 기억 셀의 기울기가 소실 없이 전파될 것으로 기대할 수 있다.

---

⏩ 다음으로는 LSTM을 파이썬을 통해 구현하고, LSTM을 사용한 언어 모델을 통해 기존 RNNLM을 개선하는 방법을 알아보겠습니다.