Neural Language Modeling

AFL·2023년 4월 8일

목록 보기

3/3

1. Language Modeling

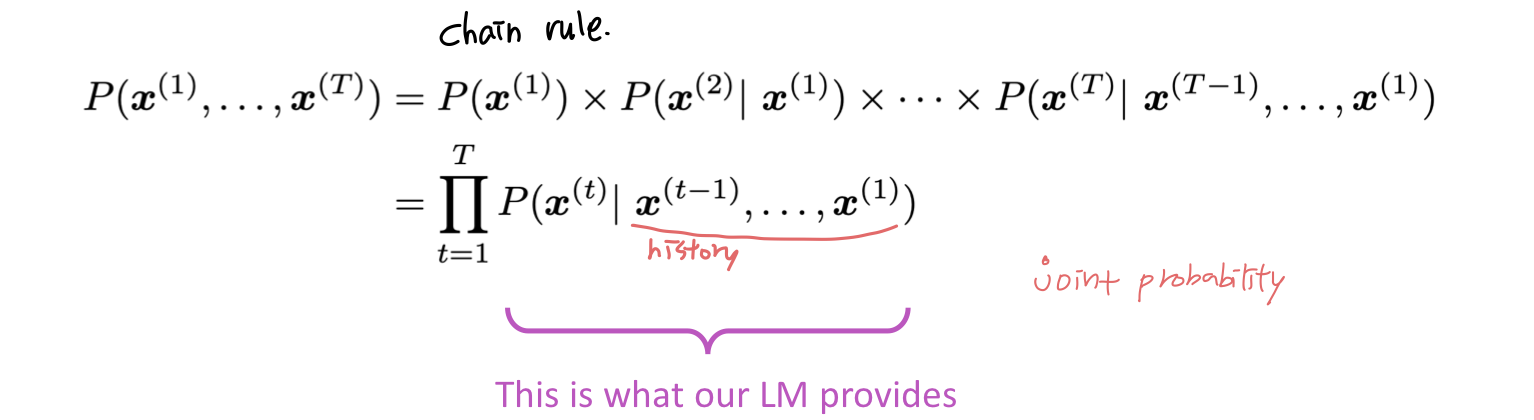
Language Modeling 은 주어진 단어들이 있을 때 다음 단어의 확률 분포를 계산하는 것이다.
$P(x^{(t+1)} | x^{(t)}, ..., x^{(1)})$
이때 $x^{(t+1)}$ 은 vocaburary $V$ 에 있는 어떤 단어든 될 수 있다.

Language Model은 piece of text 에 확률을 정해주는 시스템으로도 생각할 수 있다. 예를 들면 어떤 text들 $(X^{(t)}, ..., X^{(1)})$ 이 있다고 할 때 이 text의 확률은 다음과 같다.

n-gram Language Models

그럼 language model은 어떻게 학습할 수 있을까? 한가지 방법은 n-gram language model 로 학습하는 것이다. n-gram은 n개의 연속된 단어들의 chunk이다. 다른 n-gram이 얼마나 자주 나타나는지 통계를 내고 이것을 사용하여 다음 단어를 예측한다. 단어를 하나만 사용하면 unigram, 두개 사용하면 bigram, 세개 사용하면 trigram, ... 이다.

먼저 simpifying assumption을 만들자.: $x^{(t+1)}$ 는 그 앞의 n-1 개 단어들에만 의존한다.

그럼 n-gram 과 n-1 gram 의 확률은 어떻게 구할까? large corpus of text 에서 count한 것을 사용한다.

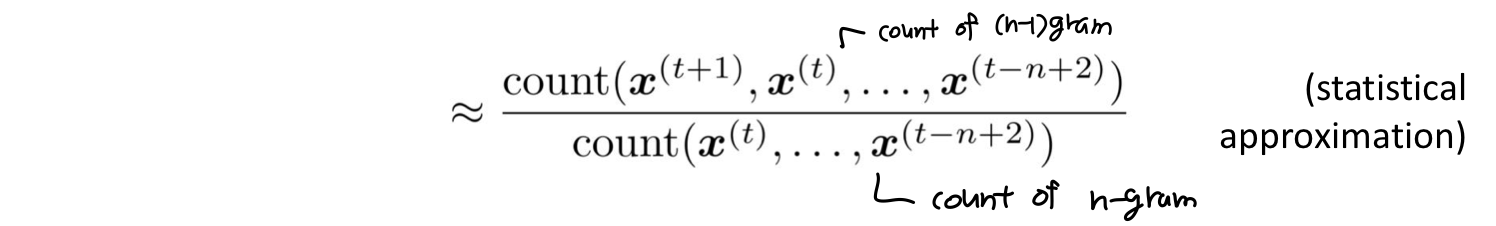
n-gram language models Example

Sparsity Problems with n-gram Language Models

"students opened their w" 가 데이터에서 한번도 안나오는 경우 어떡하지? 그러면 w는 확률이 0이 되는데ㅠㅠ
- 모든 단어들에 대해서 count할 때에 작은 델타 값을 더해주는 방법이 있다. 이 방법을 smoothing 이라고 부른다.
"students opened their" 가 데이터에서 한번도 안나오는 경우 어떡하지? 그럼 어떤 w에 대해서도 확률을 구할 수가 없는데ㅠㅠ
- "opened their" 에 대해서 찾도록 앞에 나오는 조건 문장을 줄이는 방법이 있다. 더 작은 n-gram 을 사용하겠다는 것이다. 이 방법을 backoff 라고 부른다.

=> n이 커질수록 sparsity 문제는 심해진다. 보통의 경우에 n은 커봤자 5이다.

Storage Problems with n-gram Language Models

corpus 에서 찾은 모든 n-gram 에 대해서 count를 저장해야 한다.

=> n 이 커지거나 corpus 가 커지면 Model size 도 커진다.

Generating text with a n-gram Language Model

Language Model은 text 생성에도 사용할 수 있다.

예시를 보면 문법은 잘 맞지만 맥락없다 (incoherent). 이 예시는 trigram을 사용한 것이다. 더 잘 model 하기 위해서는 n-gram의 n 의 수를 늘려야 한다. 하지만 n을 크게 하면 sparsity 문제가 심해지고 model size 도 커진다.

2. RNN

앞서 language modeling의 input, output 은 다음과 같았다.

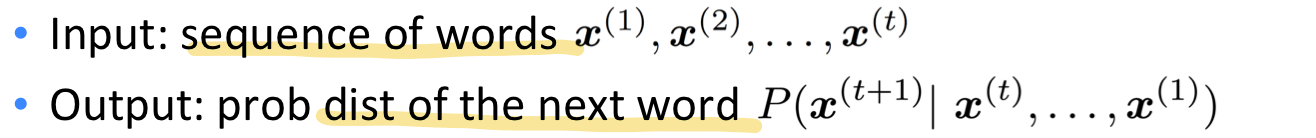
대신에 window-based neural model 을 사용하는 건 어떨까?

A fixed-window neural Language Model

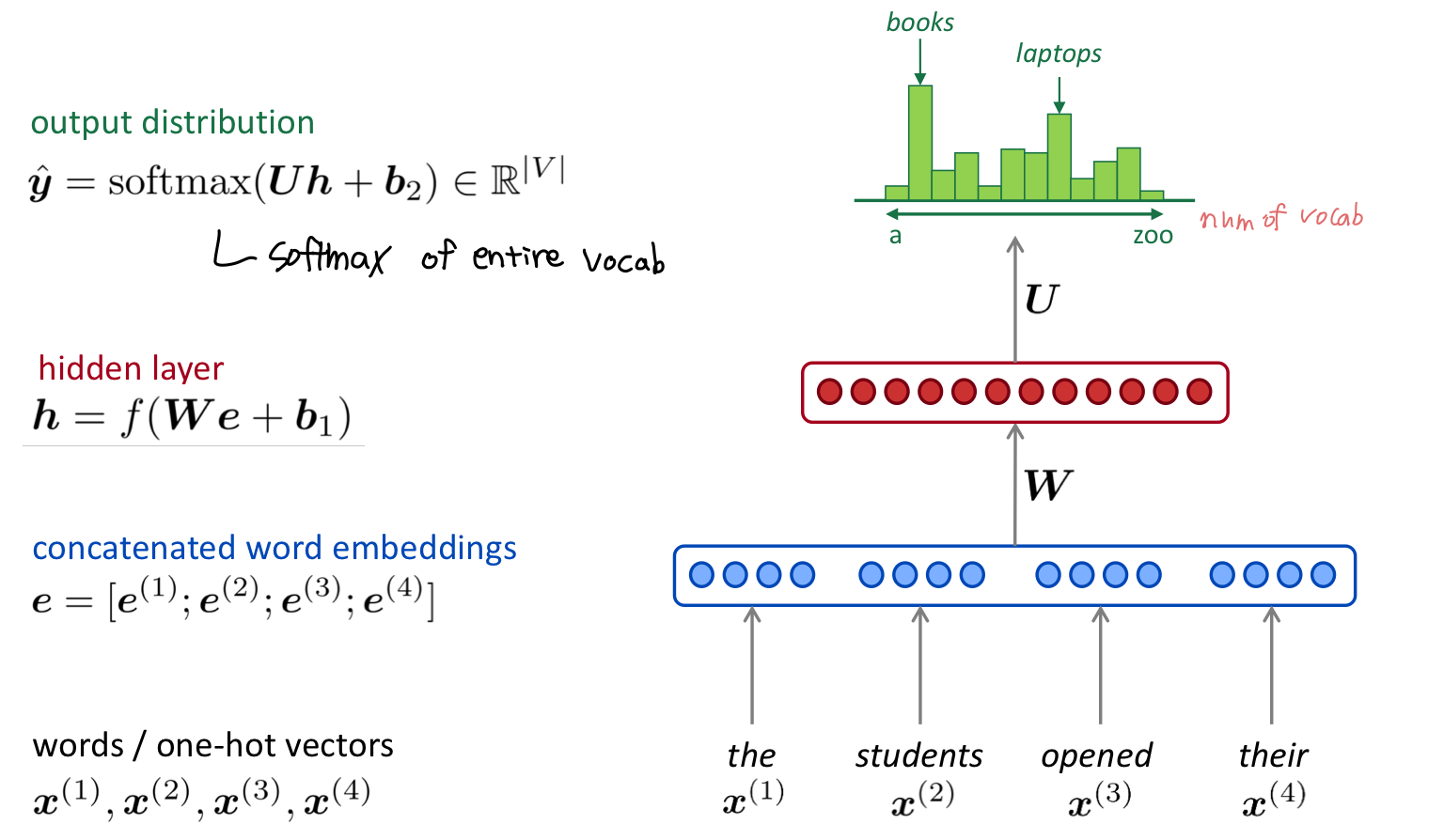
window 사이즈 만큼의 단어를 one-hot vector 형태로 입력하여 임베딩한다. 임베딩 벡터들을을 concatenate하여 가중치 값과 연산한 후 hidden layer를 통과한다. 최종적으로 softmax 함수를 통해 각 단어들의 확률 분포값을 얻을 수 있으며, 이를 통해 제일 가능서이 높은 다음 단어를 예측한다.

이와 같이 특정 개수의 단어를 Neural Network의 input으로 받는 model을 Fixed-window Neural Language Model이라고 한다.

n-gram LM 에 비해 좋아진 점
- sparsity 문제가 없어졌다.
- 모든 n-gram 을 저장할 필요가 없어졌다.

아직 해결하지 못한 문제
- fixed window가 너무 작다.
- window 를 크게 하면 W (vocab)도 커진다.
- window는 충분히 클 수 없다.
- x1과 x2 는 W에 완전히 다른 weight로 곱해진다. No symmetry.

=> 따라서 어떤 길이의 input이든 처리할 수 있는 neural architecture가 필요하다.

Recurrent Neural Networks (RNN)

어떤 길이의 input 이든 처리할 수 있는 neural architecture가 바로 RNN이다. 핵심 아이디어는 반복해서 같은 weight W 를 적용시키는 것이다.

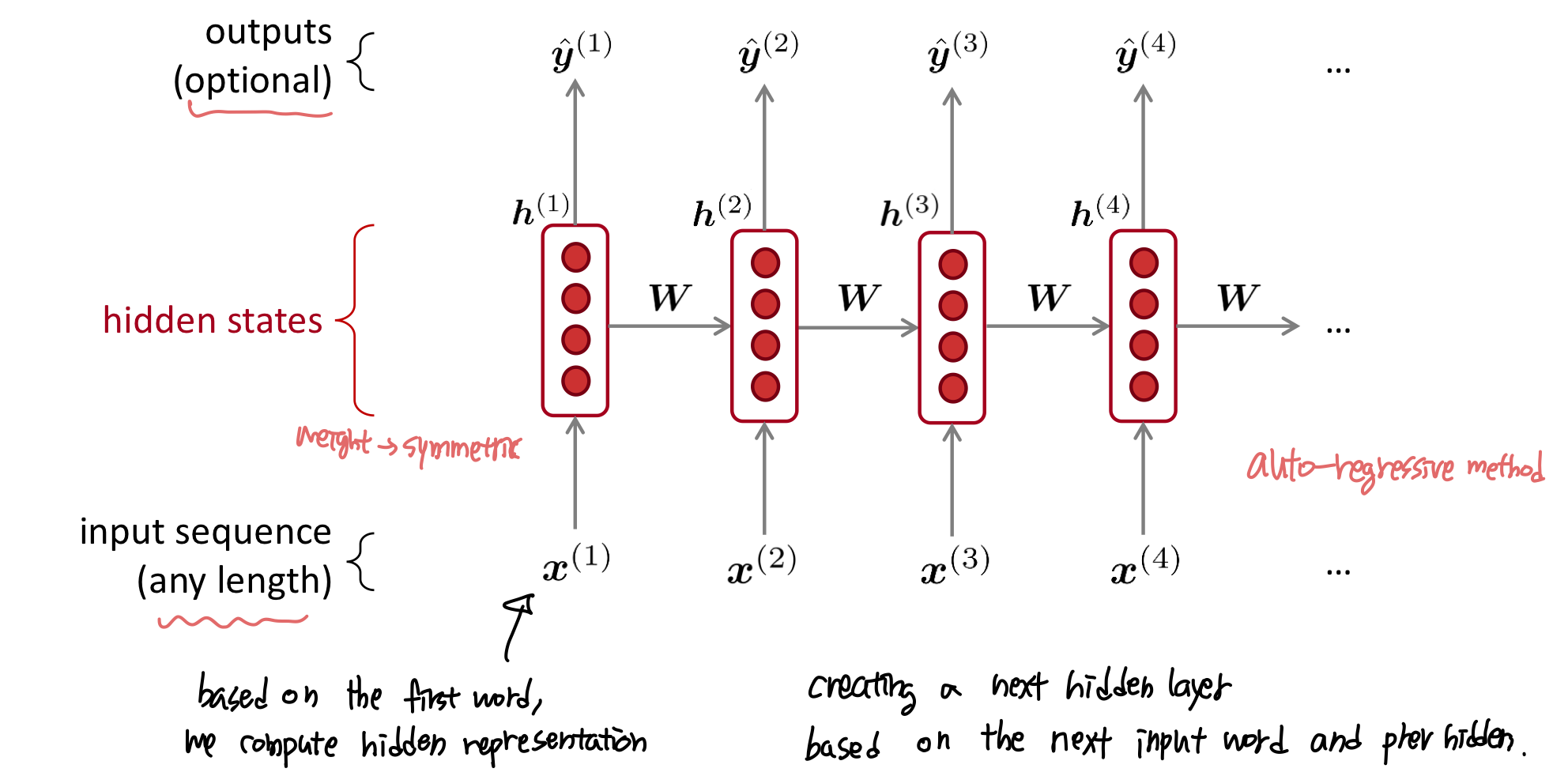
A RNN Language Model

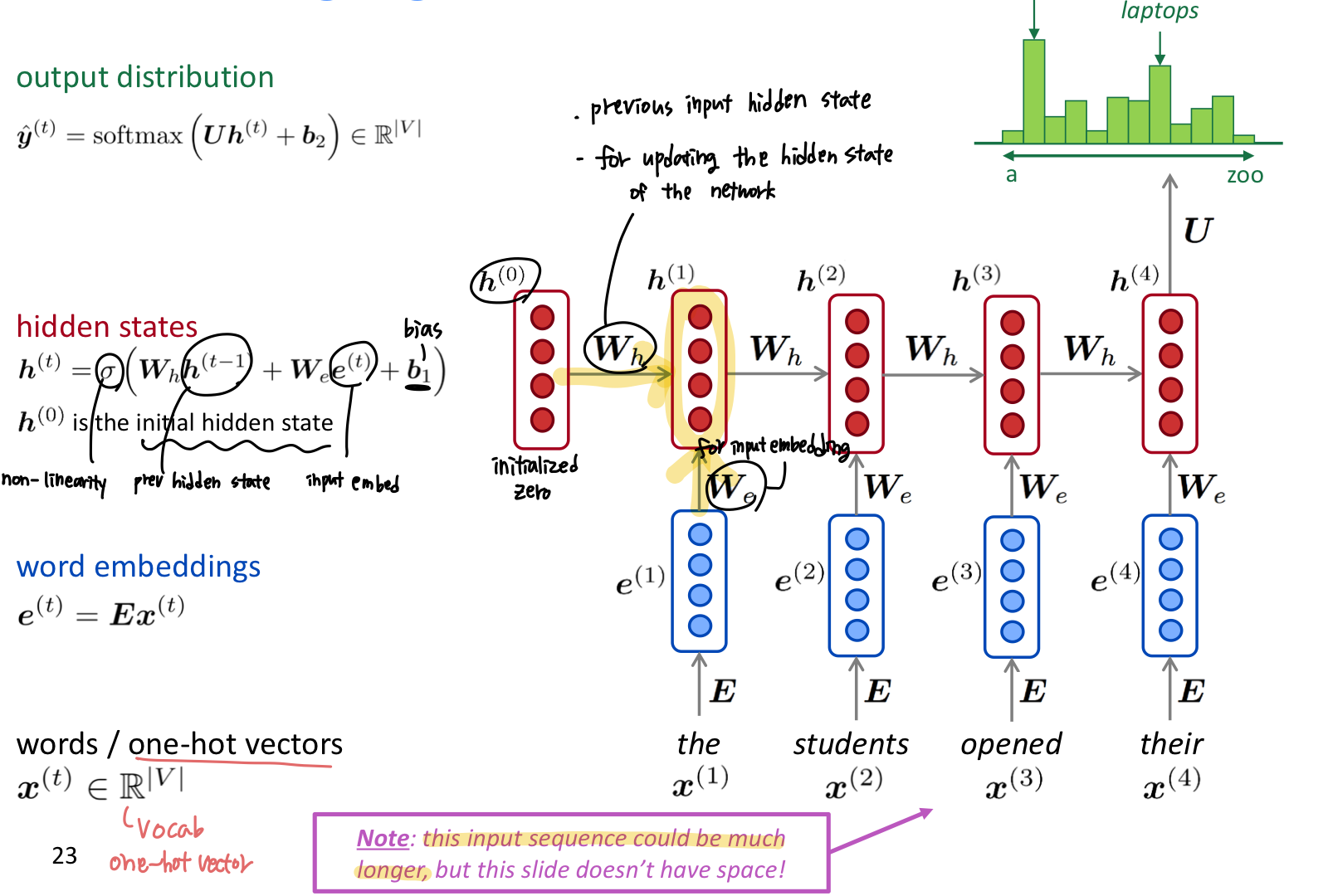
RNN의 장점
- 어떤 길이의 input이든 가능하다.
- t 시점에서 얼마든지 그 전의 정보를 사용하기 위해 step back 할 수 있다.
- input이 길다고 해서 model size가 커지지 않는다.
- 어떤 input 이든 같은 weight를 사용하기 때문에 symmetry 하다.
RNN의 단점
- recurrent 계산이 느리다.
- 많이 과거로 돌아가면 (까먹어서) 정보에 접근하기 어렵다. (vanishing gradient problem)

Training a RNN Language Model

연속적인 단어들인 big corpus of text를 가져온다.
RNN-LM 에 적용시켜서 모든 step t에 대해 output distribution y hat 을 계산한다.
step t 에서 loss function은 예측된 확률 분포 y hat 과 실제 다음 단어인 y 사이의 cross-entropy 이다.

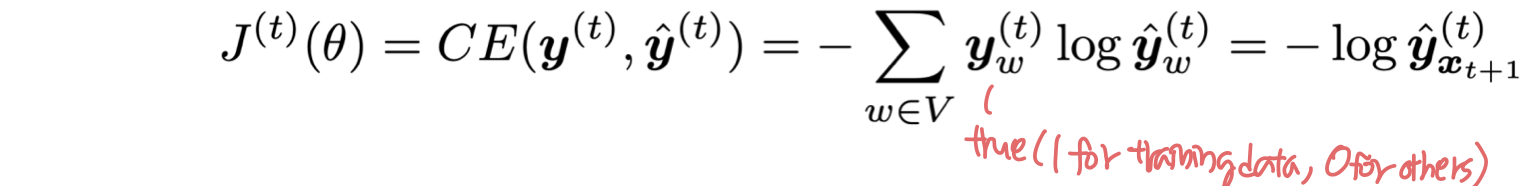
전체 training set에 대해 평균을 구해서 overall loss 를 구한다.

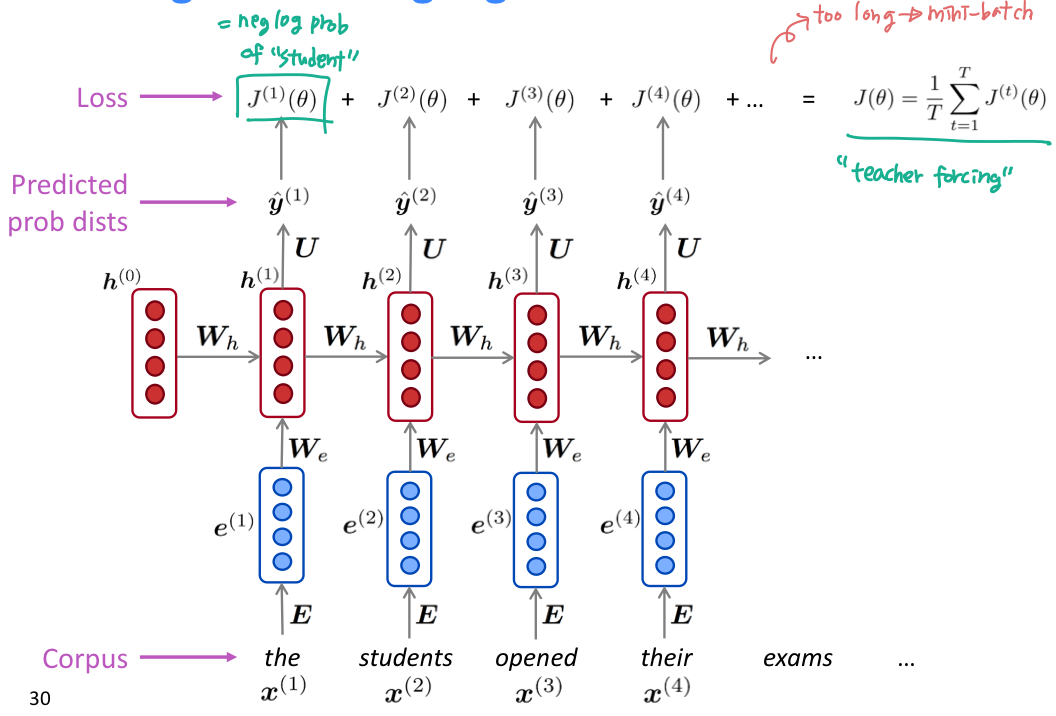
하지만 전체 corpus 에 대해서 모두 loss와 gradient 를 구하는 것은 비용이 너무 크다. 이 문제를 해결하기 위해 Stochastic Gradient Descent 를 떠올려보자. SGD 는 작은 chunk of data 에 대해 loss와 gradient 를 계산할 수 있다. loss J() 를 batch of sentence 에 대해서 계산하자!

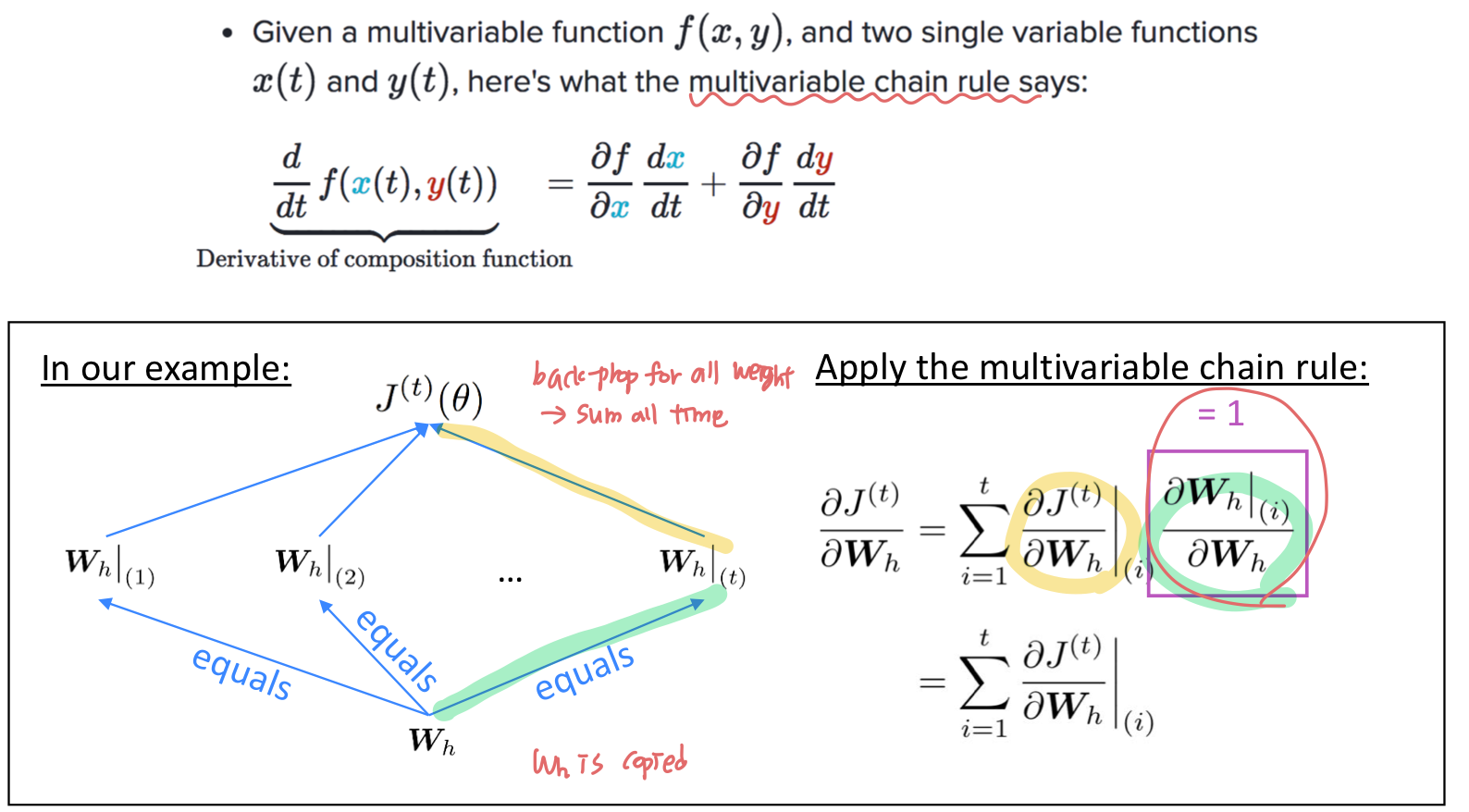
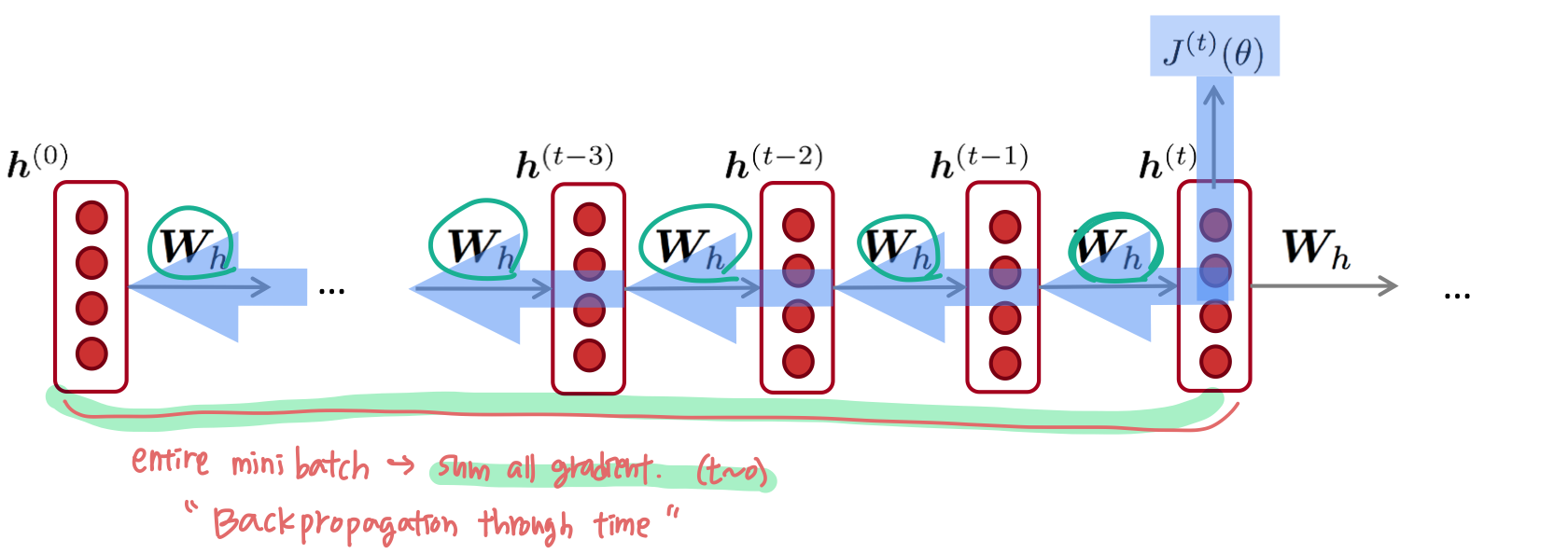
Backpropagation for RNNs

RNN에서 반복되는 weight matrix $W_h$ 에 대해 loss 를 미분한 것은, 각 시점마다 gradient를 구한 것의 합과 같다.

Generating text with a RNN Language Model

n-gram Language Model 처럼, RNN LM 도 반복되는 sampling으로 text를 생성할 수 있다. sampled 된 output 은 다음 단계의 Input이다.

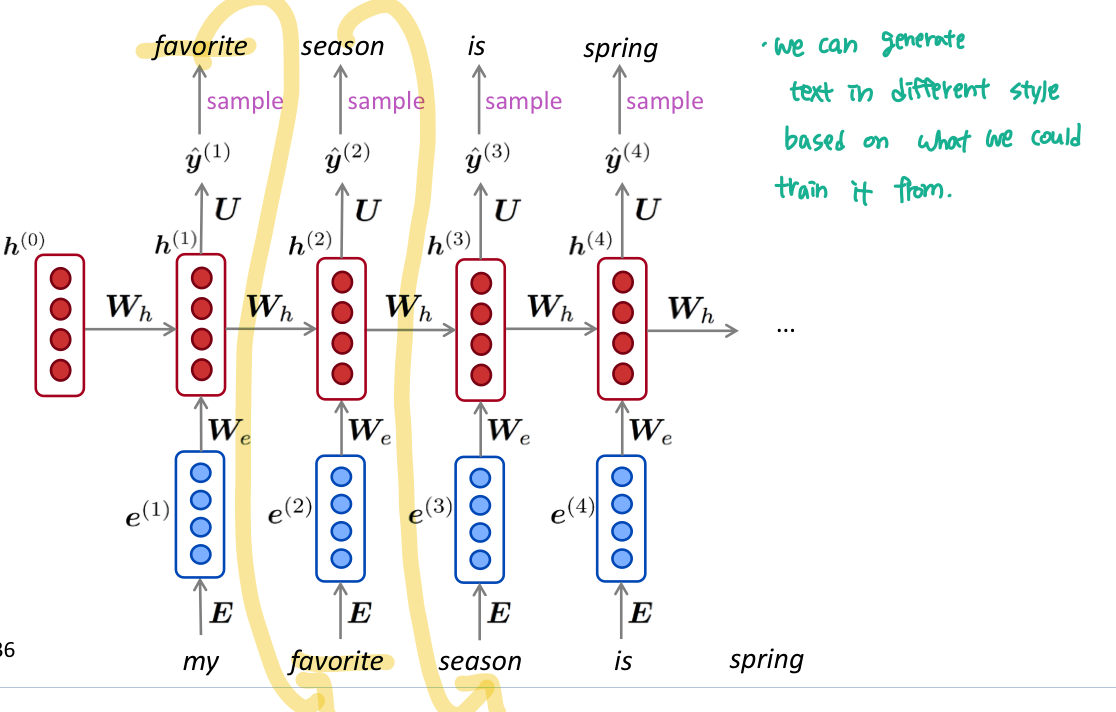
특정 종류의 text 에서 RNN-LM 을 학습시킨 다음 해당 style 의 text 를 생성할 수 있다. 예를 들면 요리 레시피로 train한 RNN-LM 으로 생성을 하면 다음과 같이 나온다.

Evaluating Language Models

language model이 좋은지 아닌지 어떻게 평가할 수 있을까? LM을 위한 standard evaluation metric은 perplexity 다. LM 을 통해 예측한 corpus의 inverse를 corpus 의 길이로 normalize 해준다.

cross-entropy loss J() 에 log 를 위한 값의 exponential 값과 같다.

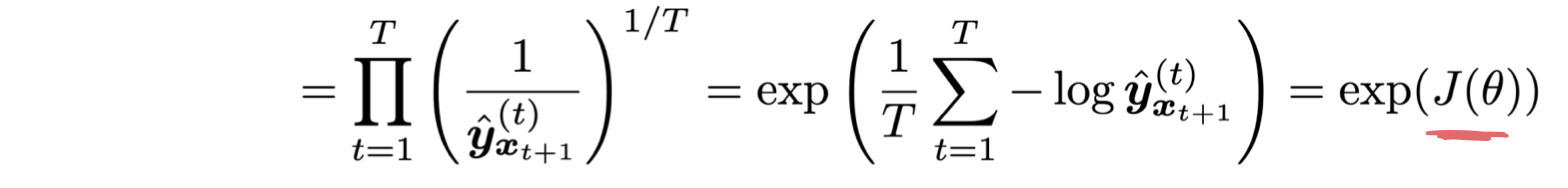
Perplexity 는 작을수록 좋다.

RNN != LM
RNN은 LM을 만들기 위한 좋은 방법이다.

RNNs can be used for ...

part-of-speech tagging

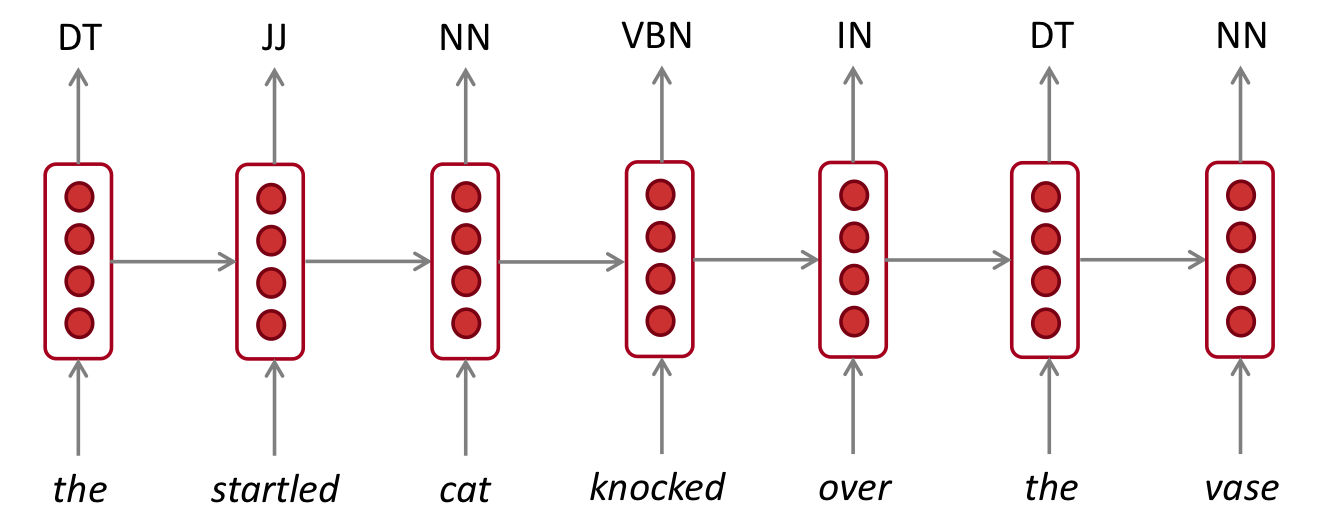
sentiment calssification

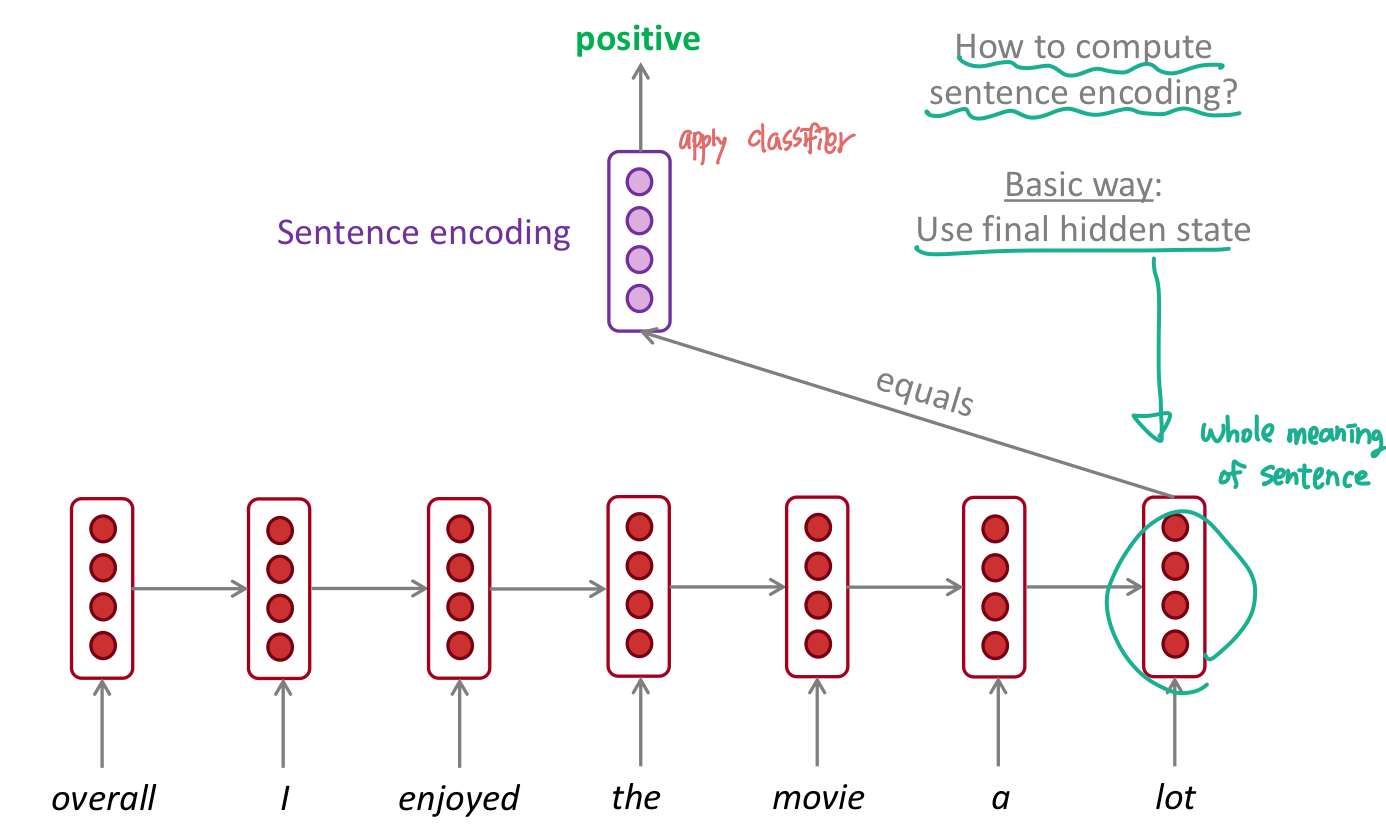
question answering

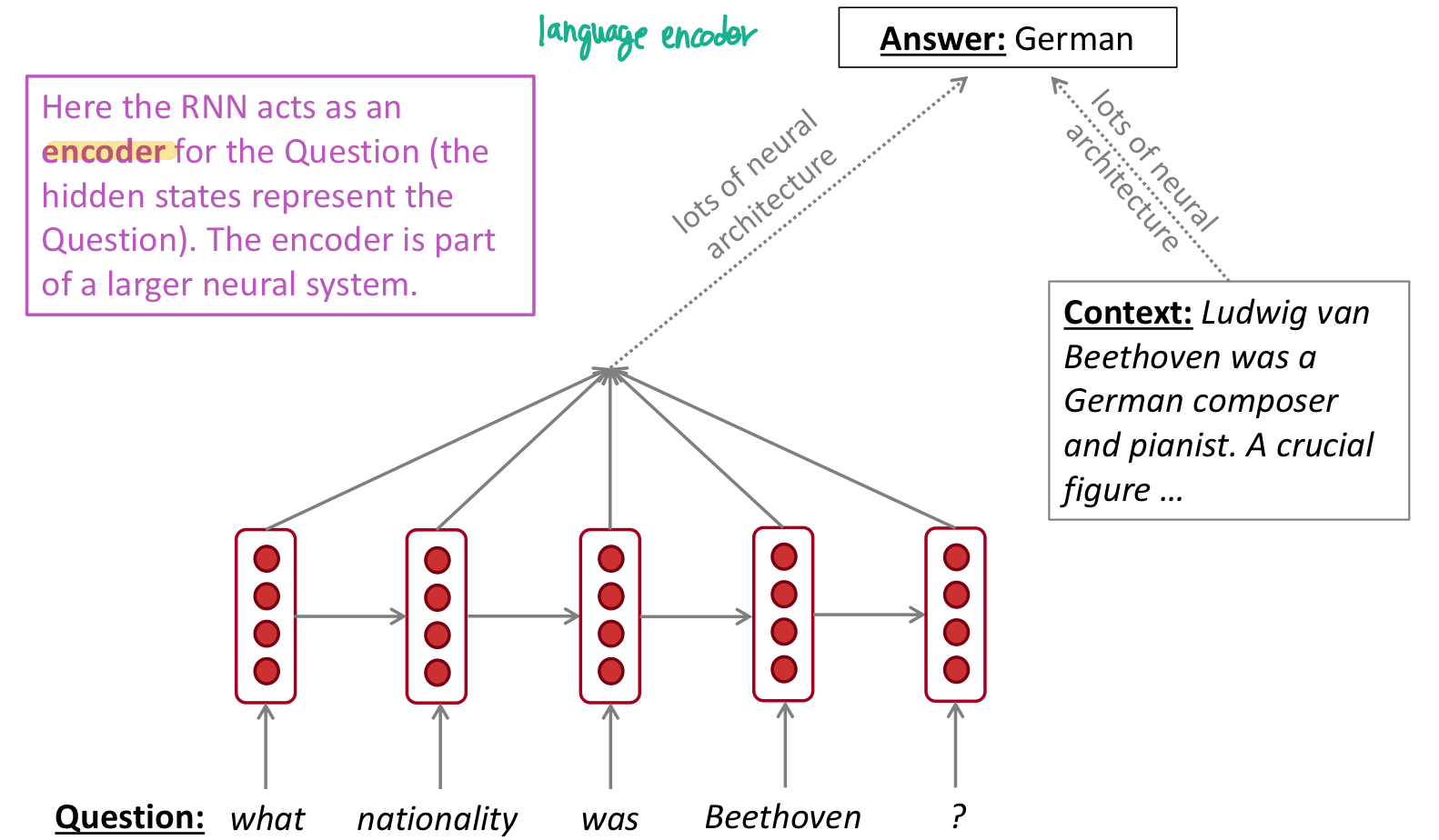
speech recognition

3. Vanishing Gradient Problem

이렇게 좋은 RNN에도 문제가 있다. 바로 vanishing gradient problem 인데 쉽게 말하면 과거로 backpropagation 하면서 정보를 까먹어버린다는 것이다. 이 문제를 해결하기 위해 만들어진 여러 방법들이 있는데 LSTM, GRU, multi-layer RNN, bidirectional RNN 이 있다.

Vanishing gradient intuition

gradient 가 너무 작으면 점점 더 backpropagate 할수록 gradient signal 이 작아지고 또 작아진다.

t 시점의 hidden state는 다음과 같다.

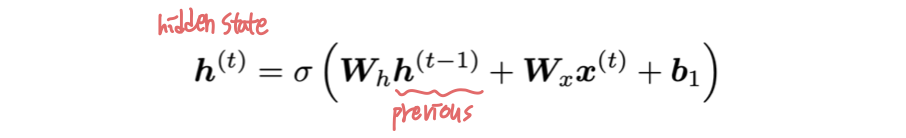
따라서 이전의 hidden state 으로 미분하면 다음과 같다.

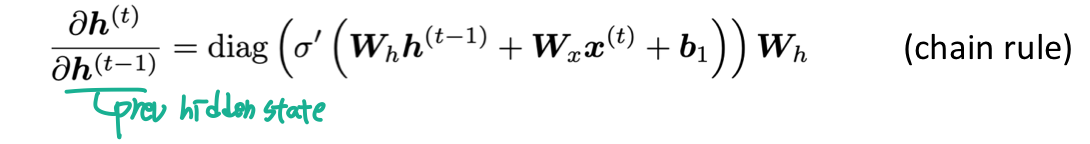
i 번째의 loss J() 를 이전 step인 j 번째 hidden state $h^{(j)}$ 에 대해 미분한 것을 보면 다음과 같다. $W_h$ 가 너무 작으면 $W_h^{(i-j)}$ 는 사라질 듯이 작아진다. $W_h^{(i-j)}$ 로 항 전체의 크기가 결정된다.

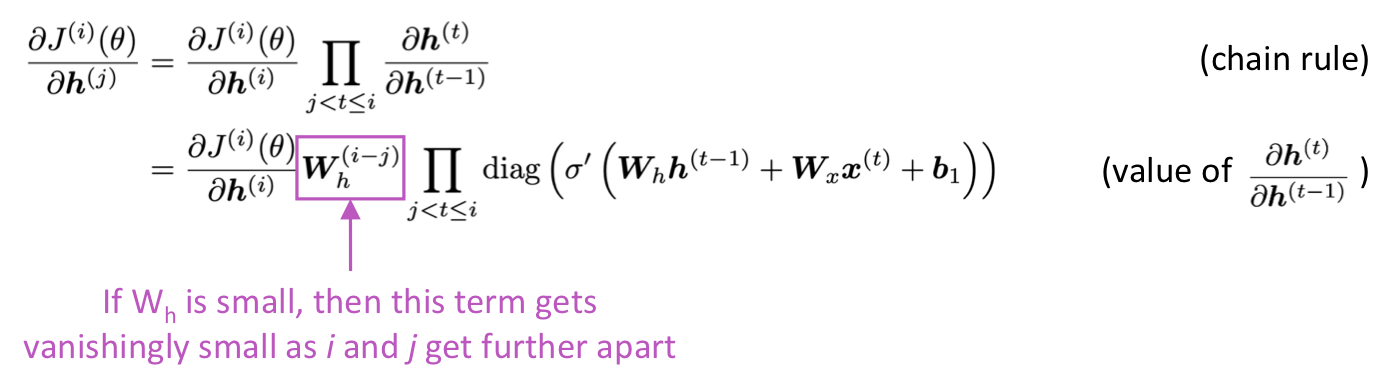
다음의 matrix L2 norm 식을 보자.

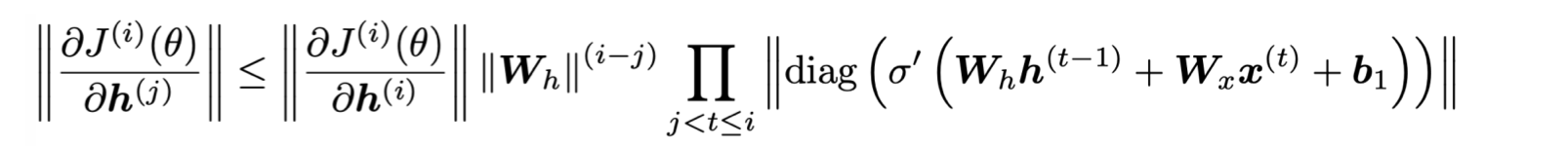
$W_h$ 의 가장 큰 eigenvalue가 1보다 작으면, $h^{(j)}$ 에 대한 $J^{(i)}(\theta)$ 의 미분은 지수적으로 줄어든다 (shrink exponentially). 또, 가장 큰 eigenvalue가 1보다 큰 경우에는 gradient 가 엄청 크게 증가한다 (exploding gradient).

왜 vanishing gradient 가 문제가 되는가?

가까이에 있는 gradient signal 보다 멀리 있는 gradient signal 이 더 작기 때문에 잃어버리게 된다. 그래서 model weight 는 가까이 있는 것에만 영향을 받고 long-term 은 영향을 못받는다.

Gradient 는 "measure of the effect of the past on the future" 라고 할 수 있다. gradient가 너무 작아져버리는 경우, 결과적으로 봤을 때 step t와 t+n 사이에 진짜로 dependency 가 없어서 gradient 가 작은 것인지, 파라미터 값이 잘못 설정되어서 gradient 가 작아져 버린 것인지 알기가 어렵다.

Effect of vanishing gradient on RNN-LM

LM task에 적용한 예를 보자.

첫 줄의 'ticket' 과 마지막에 올 target word 'ticket' 의 dependency를 모델해야한다. 하지만 gradient가 작으면 모델은 dependency 를 학습하지 못하게 되고, 따라서 test 할 때 long-distance dependency 를 예측하지 못하게 된다.

위 예제에서도 vanishing gradient 로 인해 RNN-LM 은 syntactic recency 보다 sequential recency 로부터 학습을 더 잘하게 되고, 그래서 오류가 생기게 된다.

왜 exploding gradient 가 문제가 되는가?

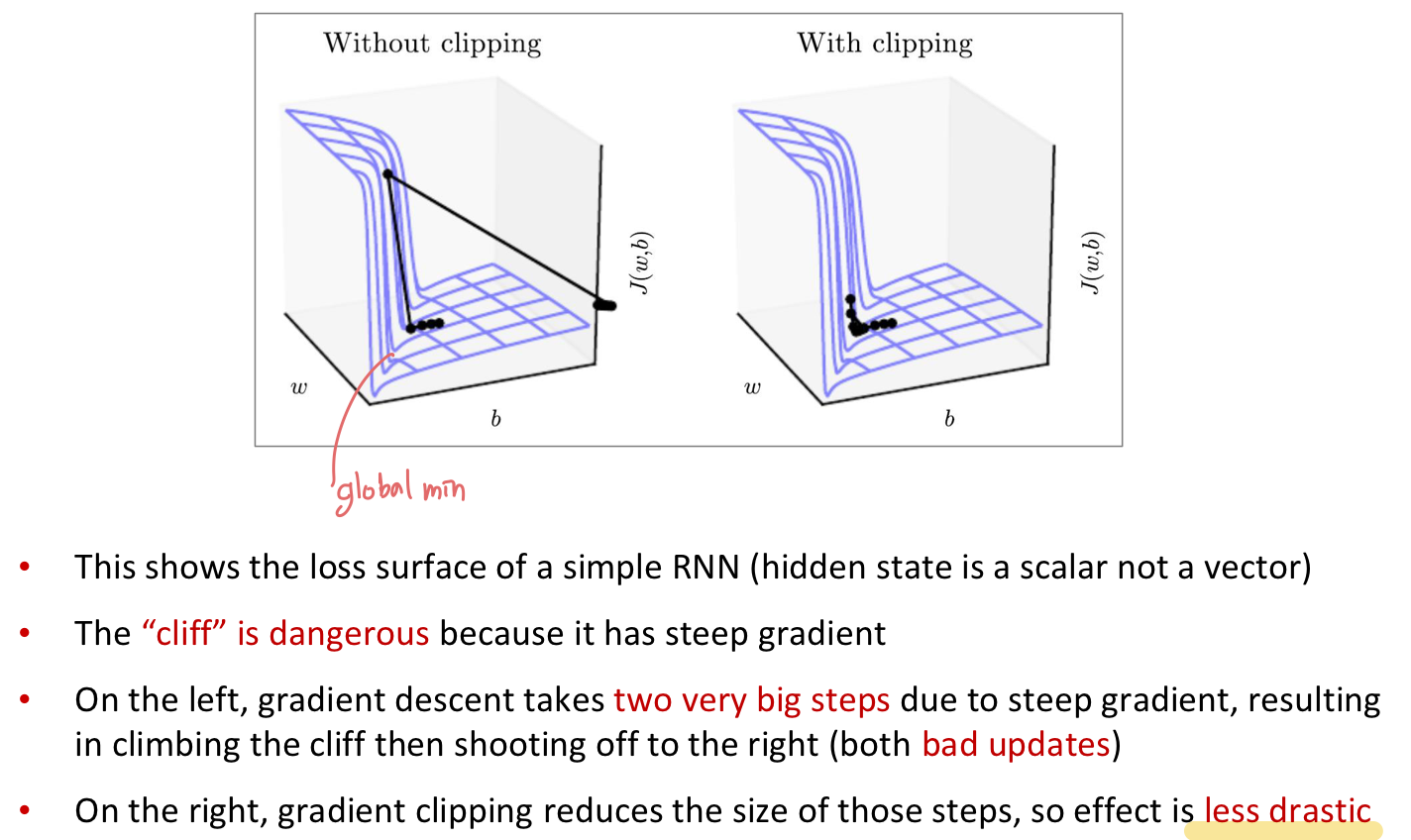
gradient가 너무 커지게 되면, SGD update step이 너무 커진다. 이런 문제를 exploding gradient problem 이라고 한다. 이 문제는 Gradient clipping 으로 해결할 수 있다.

Gradient clipping

파라미터를 update 할 때 gradient의 norm이 어떤 threshold 보다 크면, SGD update를 적용하기 전에 scale down 해주는 방법이다.

같은 방향으로 가되, 더 작은 step 으로 움직인다.

vanishing gradient 를 어떻게 해결할 수 있을까?

가장 큰 문제는 RNN이 여러번의 timestep 을 거쳐서까지 정보를 저장하고 있기가 어려렵다는 것이다. 일반적인 RNN에서 hidden state는 아래 식에서 처럼 계속해서 다시 사용되었다 ( $h^{(t-1)}$ ).

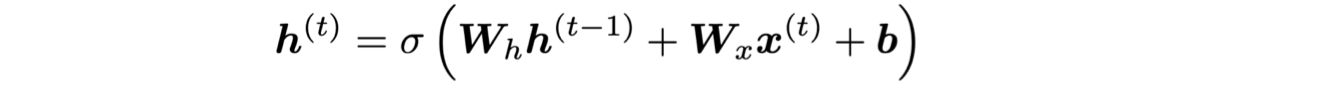
그럼, RNN을 memory를 구분해서 사용하는 방법은 어떨까 ??

LSTM (Long Short-Term Memory)

이 방법은 vanishing gradient problem 을 해결하기 위해 고안한 방법이다. step t 에 hidden state $h^{(t-1)}$ 와 cell state $c^{(t-1)}$ 이 있다.

둘다 vector 길이가 n이다.
cell은 long-term 정보를 가지고 있다.
LSTM 은 cell로부터 정보를 지우거나 쓰거나 읽을 수 있다.

어떤 정보를 지우고 쓰고 읽을 지는 세개 각각의 gate 에 따라 contol된다.

gate 는 vector 길이가 n 이다.
각 timestep 마다, gate의 각 element는 open (1), close (0), 또는 그 사이의 상태일 수 있다.
gate 는 dynamic 하다.: 값이 현재에 학습하고 있는 데이터의 context를 기반으로 계산된다.

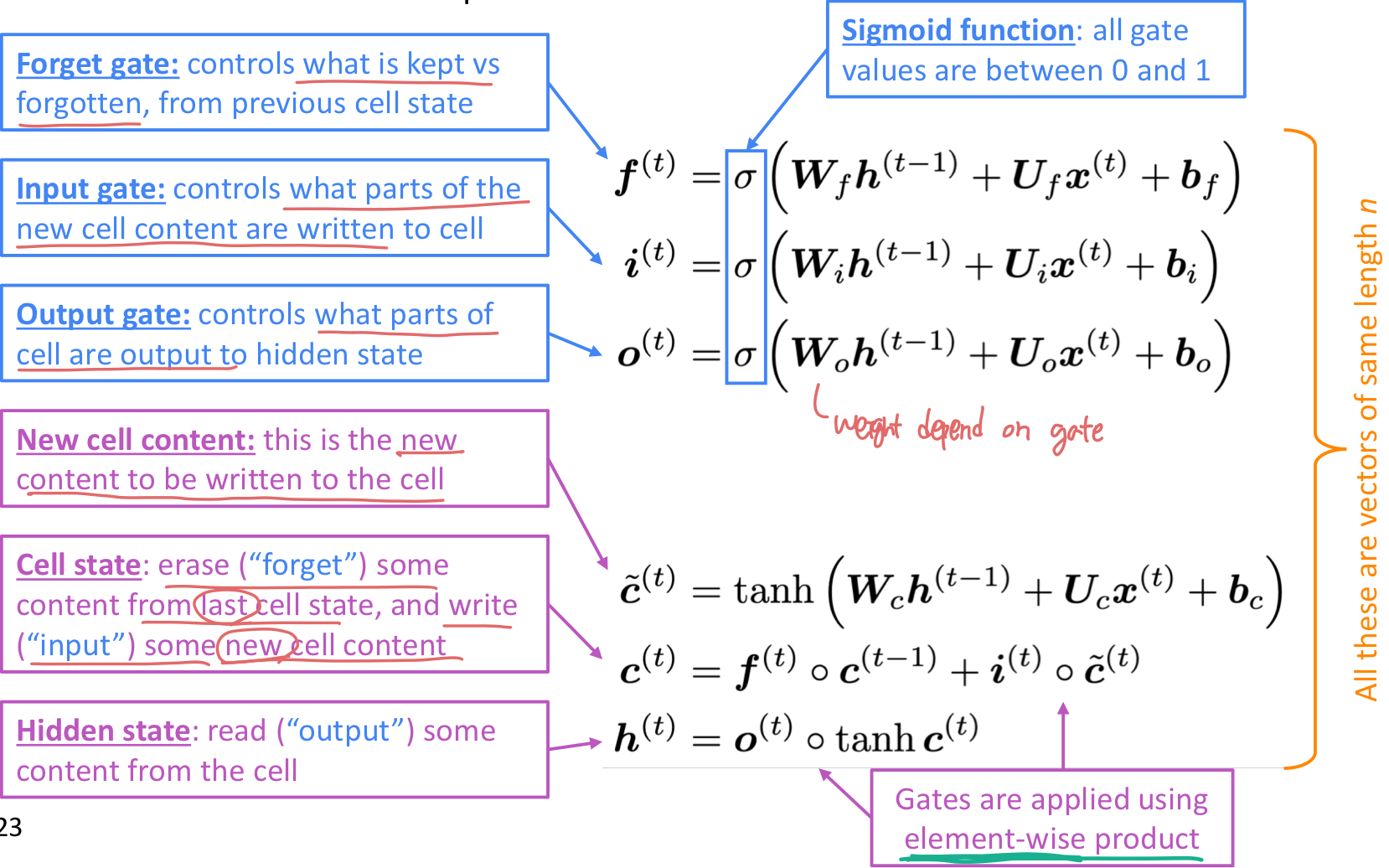
세 개의 gate는 forget, input, output 이 있다.

forget gate
- 이전의 cell state로 부터 어떤 정보를 반영하고, 어떤 정보를 잊을지 결정하는 gate이다.
input gate
- 어떤 새로운 정보가 cell state에 저장될 지 결정하는 gate이다.
output gate
- 어떤 cell이 hidden state에 output으로 할 지 결정하는 gate이다.

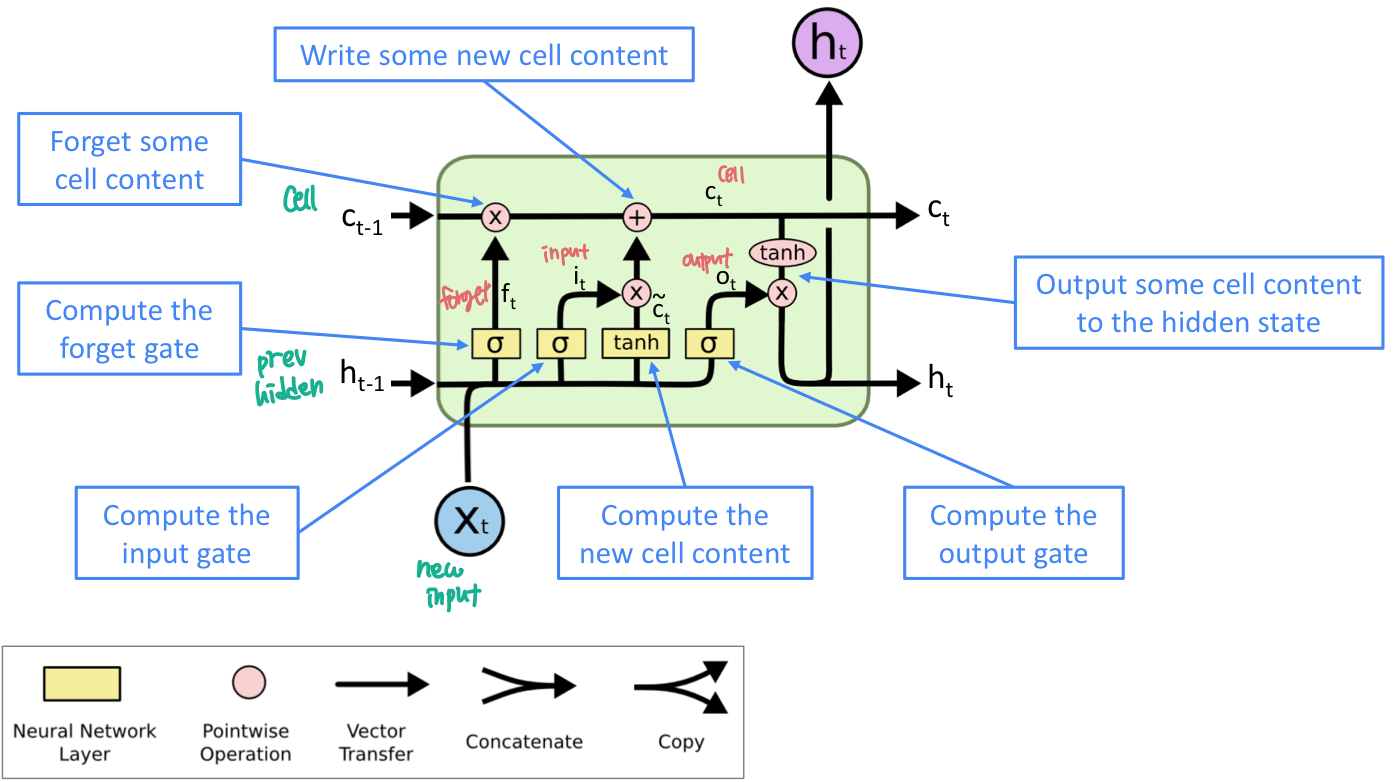
LSTM 이 vanishing gradient를 어떻게 해결했나?

LSTM은 RNN이 여러 timestep 에 거쳐서 정보를 잘 보존할 수 있게 한다.
- LSTM은 forget gate 에서 모든걸 기억하도록 하면 cell에 있는 정보를 기억하고 있다. 반면에 일반적인 RNN은 hidden state가 저장하고 있는 recurrent weight matric $W_h$ 를 기억하고 있기 어렵다.
LSTM은 vanishing/exploding gardient가 없다고 보장은 못하지만 long-distance dependency를 학습할 수 있는 것은 확실하다.

GRU (Gated Recurrent Units)

LSTM의 간단한 버전으로 GRU 를 고안했다. LSTM의 강점을 가져오되, 불필요한 복잡성을 제거한 모델이다. 각 timestep t 마다 input $x^t$ 와 hidden state $h^t$ 가 있고, cell state 는 없다.

두개의 gate 가 있다.

Update gate
- hidden state의 어떤 부분을 update 하고 preserve 할지 결정한다.
Reset gate
- 새로운 content 를 계산할 때 previous hidden state의 어떤 부분을 사용할 것인지 결정한다.

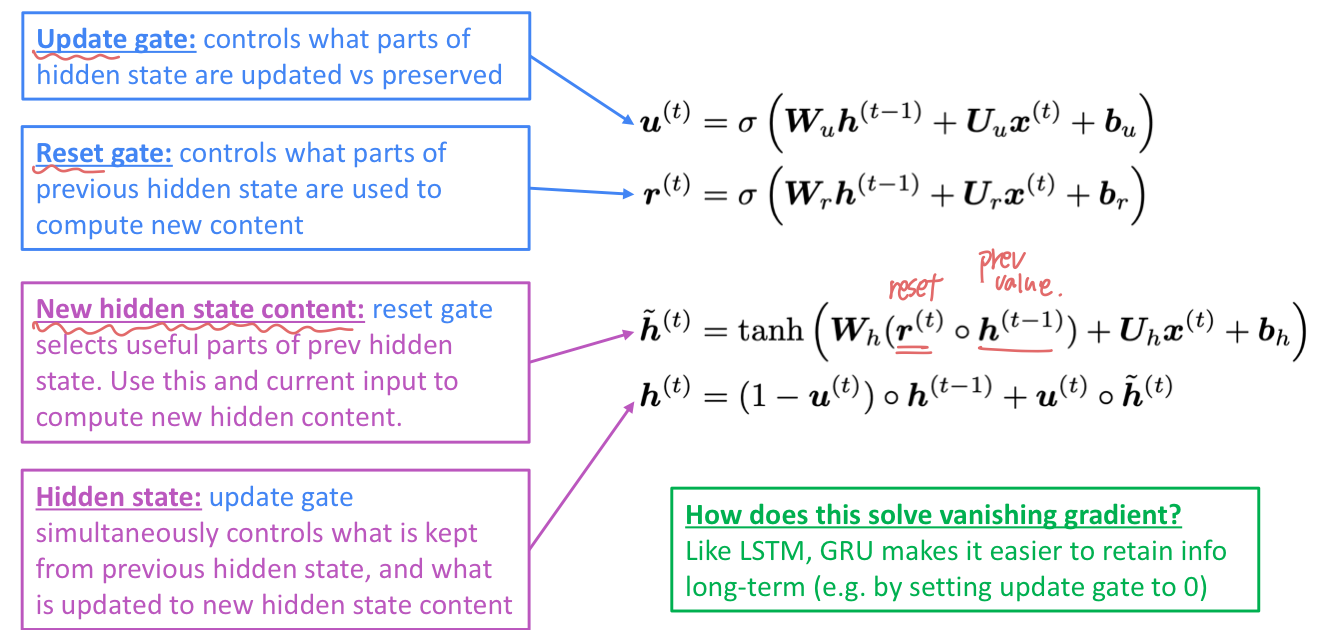
LSTM vs. GRU

GRU 가 더 계산이 빠르고 파라미터 수가 더 적다.
어느 하나가 더 낫다는 결런은 없다.
데이터가 long dependency 이거나 trainign data가 많은 경우에는 주로 LSTM이 좋은 기본 선택이다.
Rule of thumb: LSTM 으로 시작해서 더 효율적인 방법을 원할 때 GRU사용하는 방법.

Vanishing/Exploding gradient 가 RNN 만의 문제인가?

아니다! 어떤 neural archietcure든 (feed-forward, convolution도) 문제가 될 수 있다. 특히 deep 한 구조라면 더더욱!

chain rule, non-linearity function 의 선택 때문에 gradient 는 backpropagate 함에 따라 점점 더 작아질 수 있다.
따라서 lower layer는 더 느리게 학습하게 된다.
해결방법으로, direct connection (skip connection)을 더 추가한다.

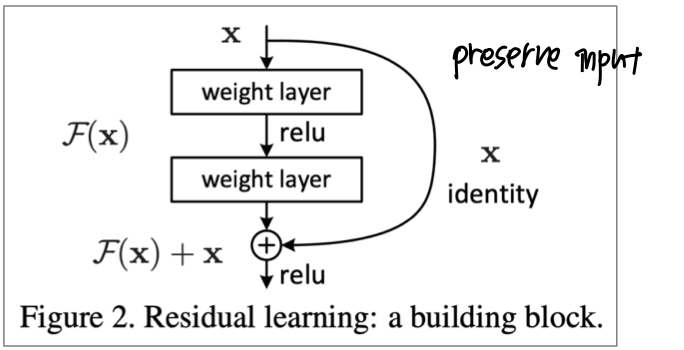
ResNet

Residual connection 인 ResNet이 그 중 하나다.
skip-connection 으로도 알려져있다.
identity conenction이 default로 정보를 저장하고 있는다.
deep network를 더 쉽게 학습할 수 있게 해준다.

DenseNet

dense connection
이전 layer들의 feature map을 계속해서 다음 layer의 입력과 연결하는 방식이다.

HighwayNet

Highway connection
residual connection과 비슷하지만 identity connection과 transformer layer 중 무엇을 사용할 지가 dynamic gate 에 의해 결정된다.

이처럼 Vanishing gradient문제는 여러 분야에서 매우 general한 문제이지만, 특히 RNN과 같이 동일한 weight matrix를 반복적으로 곱하는 모델은 특히 더 불안정하므로, 더 심각한 문제이다.

4. More fancy RNN variants

Bidirectional RNNs

문장을 left, right 두 방향 모두 정보를 이용하기 위한 방법이다.

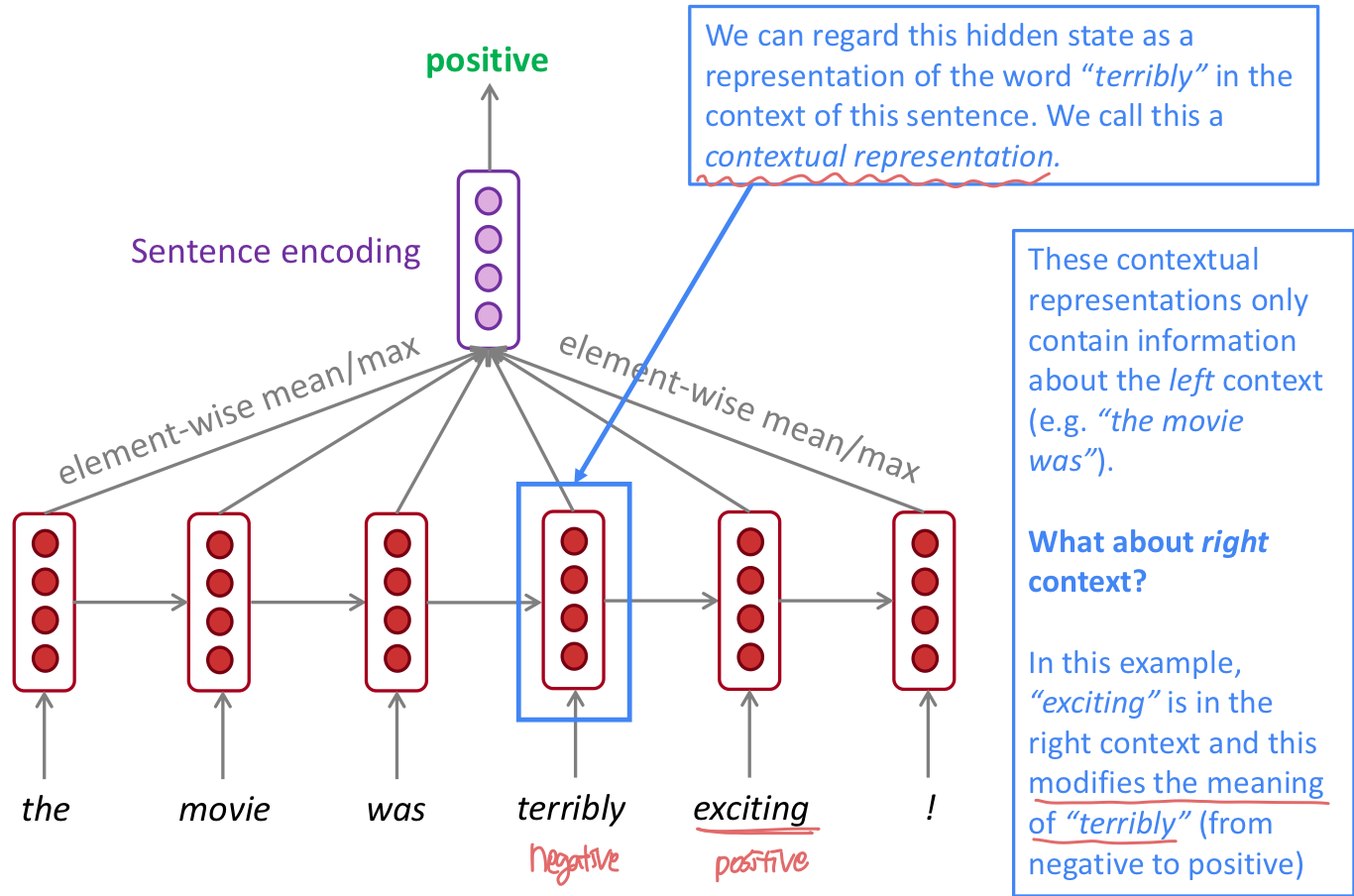
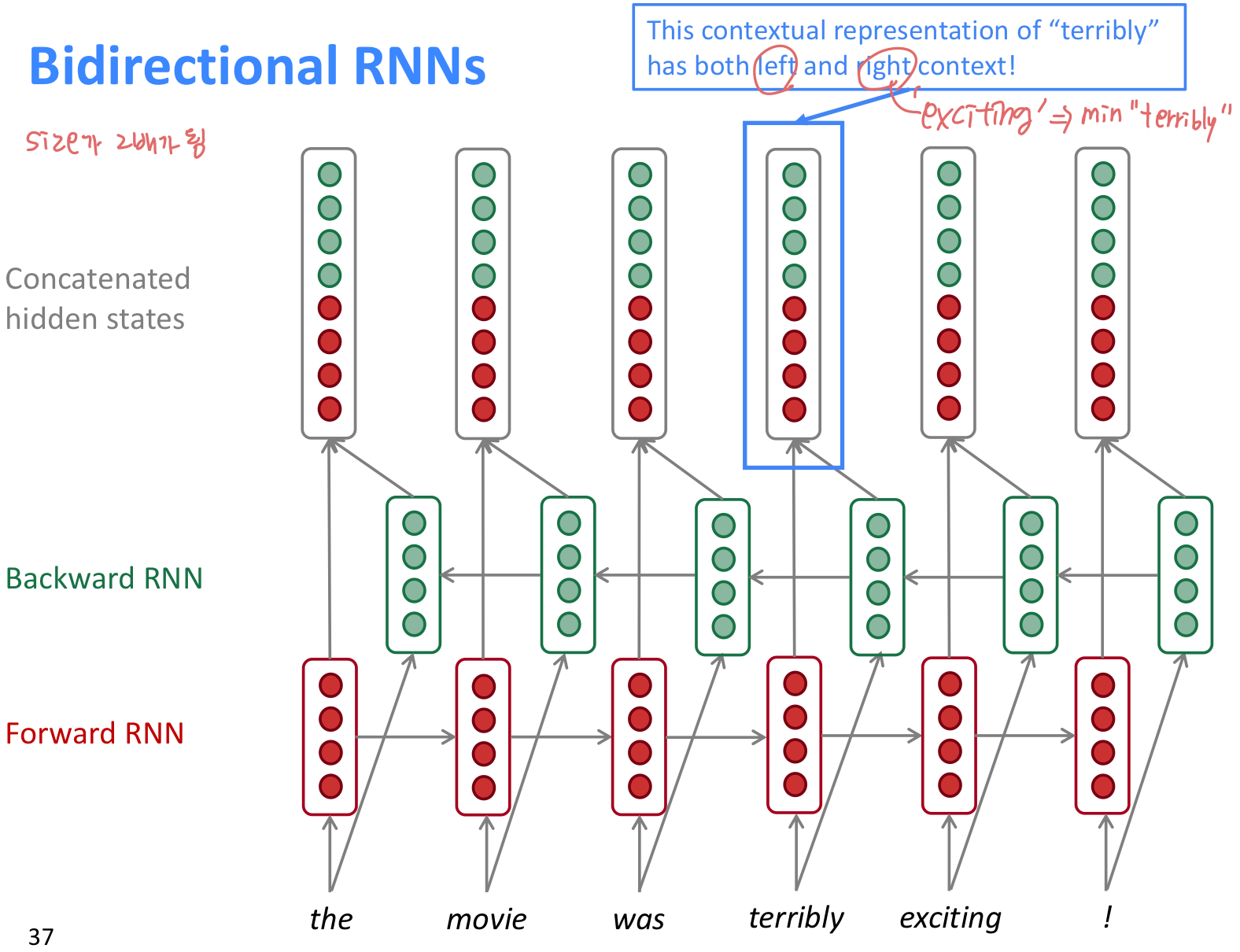
Bidirectional RNN은 문장 전체 sequence 를 가지고 있어야 적용가능하다. 그래서 Language Modeling 에는 적절하지 않다. LM은 left context 만 가지고 있기 때문이다.

문장 전체 sequence 를 input으로 가지고 있는 경우, dibirectionality 는 강력하다.
예로, BERT (Bidirectional Encoder Representatiosn from Transformers) 는 dibirectionality 를 기반으로 만들어진 강력한 pretrained contextual representation system 이다.

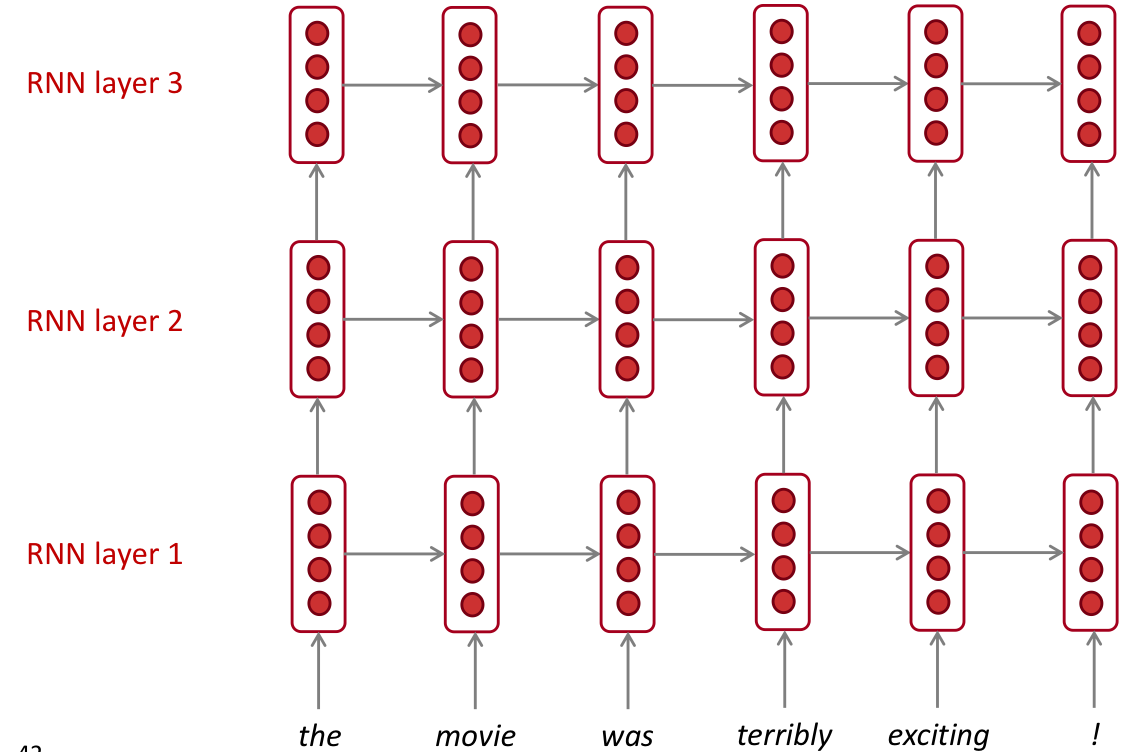
Multi-layer RNNs

RNN을 여러 층으로 사용해서 더 deep 하게 사용할 수 있다. 이를 multi-layer RNN 이라고 한다.
이런 network는 더 복잡한 표현을 계산할 수 있게 해준다.
- lower RNN은 lower level feature를, higher RNN은 higher-level feature를 학습할 수 있다.
Multi-layer RNN 을 stacked RNN 이라고 한다.
성능이 좋은 RNN은 대부분 multi-layer 이다. 보통 2~4 개의 layer를 쌓는다.
Transoremr-based network는 최대 24개 layer를 사용할 수 있다.

[Reference]

AFL

공부해서 남주자

이전 포스트