AI&DS - Algorithm(1)
Algorithm
- Algorithm is
- unambigous specification of how to solve a class of problems
- procedure or rule for solving a problem, based on conducting a sequence of specified actions
- step by step method of solving a problem
- a computer program is an algorithm
- Success stories of Algorithms are
- Link analysis
- Graph Traversal
- Sorting
- Binary Searching
- Hashing
- Data Compression
- Computational Efficiency
- 우리는 컴퓨터에서 실행할 알고리즘(data structure)을 디자인한다.
- 문제를 풀 여러 알고리즘이 있을 때 어떤 알고리즘이 나을까? 아니, 어떤 알고리즘이 더 빠를까?
- 기본 operation +, - *, ... 는 constant time (O(1)) 걸린다고 하자.
- input size 관점에서 알고리즘이 실행하는 기본 operation 은 몇개 인지를 보자.
-
Example
-
Fibonacci Numbers - FIB1(n)
if n = 0 then return 0 else if n = 1 then return 1 return FIB1(n − 1) + FIB1(n − 2) -
이 코드에 대해 다음 질문을 하게된다.
- Is it correct
- How much time does it take, as a function T(n) of n?
- Can we do better?
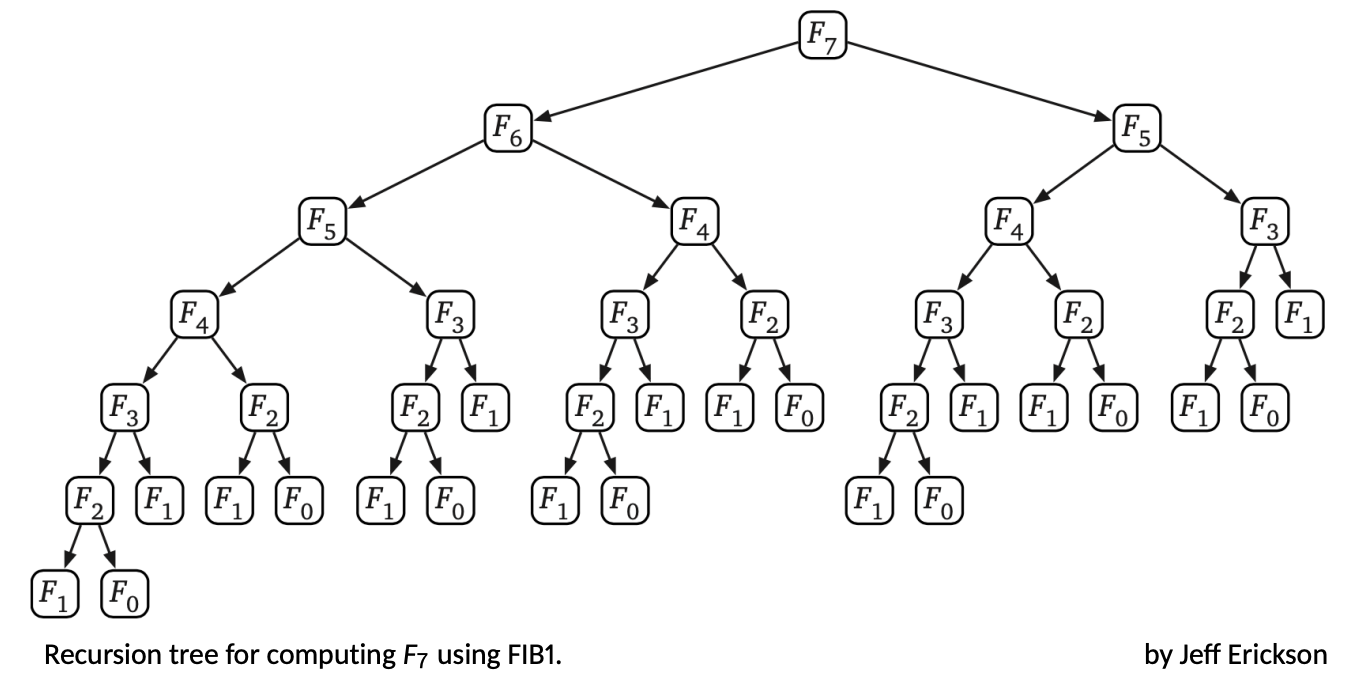
=> O(2^n) or exponential
-
Fibonacci Numbers - FIB2(n)
if n = 0 then return 0 create an array f[0, ... , n] f[0] = 0, f[1] = 1 for i = 2, ... , n do f[i] = f[i − 1] + f[i − 2] return f[n]
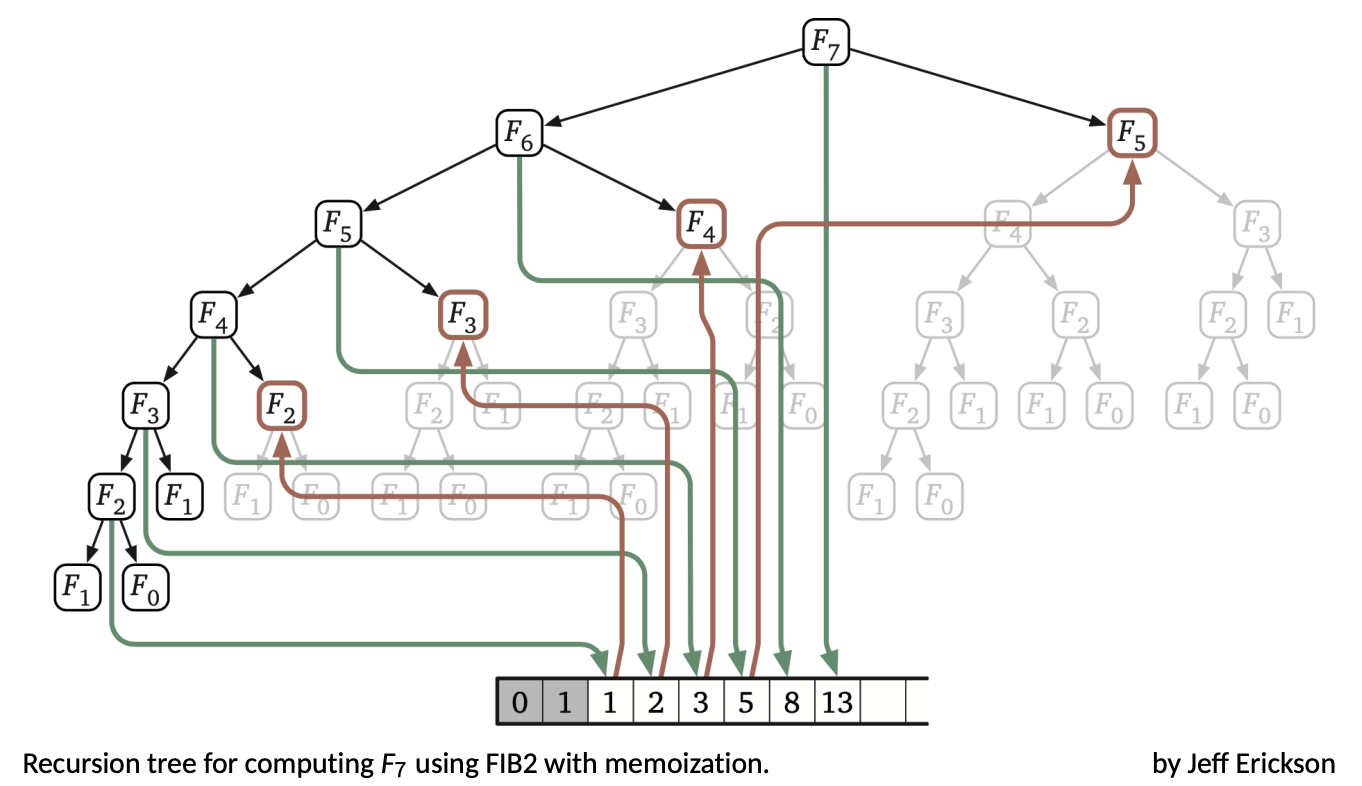
=> O(n)
-
- PageRank Algorithm
- Google research wanted to measure relative importance of website
-
Search Problems
-
P and NP
- P: Polynomial
- NP: Nondeterministic Polynomial time
- A solution to any search problem can be found and verified in polynomial time by a nondeterministic algorithm.
- A nondeterministic algorithm may exhibit different behaviors on different runs even for the same input. Nondeterministic poly-time means an algorithm may run in polytime or exponential time depending on the choices it makes during execution.
(1) Satisfiability (SAT)
An instance of SAT is a Boolean formula in CNF (conjunctive normal form).
SAT problem: Given a Boolean formula in CNF, either find a satisfying true assignment or report “none exists”.
SAT is a typical search problem: We are given an instance I, and we are asked to find a solution S.
Property of a search problem: Any proposed solution S to an instance I can be quickly checked for correctness. That is, there is a polynomial-time algorithm that takes as input I and S, and decides whether or not S is a solution for I.
지난 50년 동안 효과적인 방법을 찾으려고 했지만 성공하지 못했다. 가장 빠른 알고리즘도 지수만큼 최악이다. But, interestingly, there are two natural variants of SAT for which we have good algorithms.
-
Horn formula. All clauses contain at most one positive literal. A greedy algorithm can find a solution in linear time.
-
2SAT. All clauses have only two literals. Can be solved in linear time by finding the strongly connected components.
(2) Traveling Salesman Problem (TSP)
An instance of TSP consists of n vertices and all n(n−1)=2 distances between them.
TSP problem. Given a set of n vertices and their pairwise distances, find a shortest tour (a permutation of vertices) that passes through every vertex exactly once.
TSP as a Search problem. Given a set of n vertices, their pairwise distances, and a budget b, find a tour of total cost b or less that passes through every vertex exactly once, or report “no such tour exists”.
A dynamic programming algorithm takes O((n^2)*(2^n)) time, which is slightly better than (n − 1)!. But no polynomial time algorithm is known yet.
(3) Rudrata (Hamilton) Cycle Problem
Euler Path problem: Given a graph, find a path that contains each edge (선) exactly once.
Euler Path: A connected undirected graph has an Eulerian cycle iff every vertex has even degree.
Rudrata Cycle problem: Given a graph, find a cycle that passes through every vertex (꼭지점) exactly once.
There are two differences from the Euler problem.
– Euler’s problem visits all edges while Rudrata’s visits all vertices.
– Euler’s demands a path while Rudrata’s requires a cycle.
This is a reminiscent of the TSP, and indeed no polynomial time algorithms is known for it. But a proposed solution can be quickly checked.
(4) Balanced Cut
A cut is a set of edges whose removal leaves a graph disconnected.
Minimum Cut problem: Given a graph and a budget b, find a cut with at most b edges.
Balanced Cut problem: Given a graph with n vertices and a budget b, find a cut (A, B) such that |A|, |B| >= n/3 and at most b edges in the cut.
Balanced cuts arise in a variety of important applications, such as clustering and and image segmentation. However, no polynomial-time algorithm is known for it. But a proposed solution can be quickly checked.
(5) 3D Matching
3D Matching problem: Given n boys and n girls but also n pets, and the compatibility among them, find n disjoint triples
(6) Independent Set, Vertex Cover, Clique
Independent Set problem: Given a graph and a goal g, find g vertices that are independent, that is, no two of which have an edge between them.
Vertex Cover problem: Given a graph and a budget b, find b vertices that cover (touch) every edge
Clique problem: Given a graph with n vertices and a budget b, find a set of b vertices such that all possible edges between them are present.
(7) Longest Path, Subset Sum
Longest Path (aka Taxicab Rip-off) problem: Given a graph with nonnegative edge weights and two vertices s and t, along with a goal g, find a simple path from s to t with total weight at least g.
Subset Sum problem: Given a set of integers and a value W, find a subset of integers that adds up to exactly W.
- NP-Complete Problems
-
Property of a search problem: Any propsed solution S to an instance I can be quickly checked for correctness.
- NP : the class of all search problems.
- P : the class of all search problems that can be solved in polynomial time. Most of search problems we have considered belong to P.
-
Most researchers believe P != NP. But no proof. Then why they believe so?
-
Reduction provides some evidence
-
Reduction, A → B, has two purposes :
- (1) We know how to solve B efficiently, and want to use this to solve A.
- (2) We know A is hard, and use the reduction to prove B is hard as well.
-
-
Reductions have the composition property: If A → B and B → C, then A → C
-
A search problem is NP-complete if all other search problems reduce to it.

