학습 주제
탐욕법 (Greedy) 이용한 문제 풀이

학습 내용

• 지문에서 문제를 도출
• 어떤 알고리즘을 구성할지
• 코드로 어떻게 구현이 가능한지
• 복잡도 측면은 어떠한지
  알아본다.

• <= 전체학생 수 <= 30
• 중복되는 번호는 없음
• 여벌 체육복을 가져온 학생도 도난 당했을 수 있음 -> 2벌 -> 1벌이 되어 자신은 듣고, 다른 학생에게는 주지 못함.
  

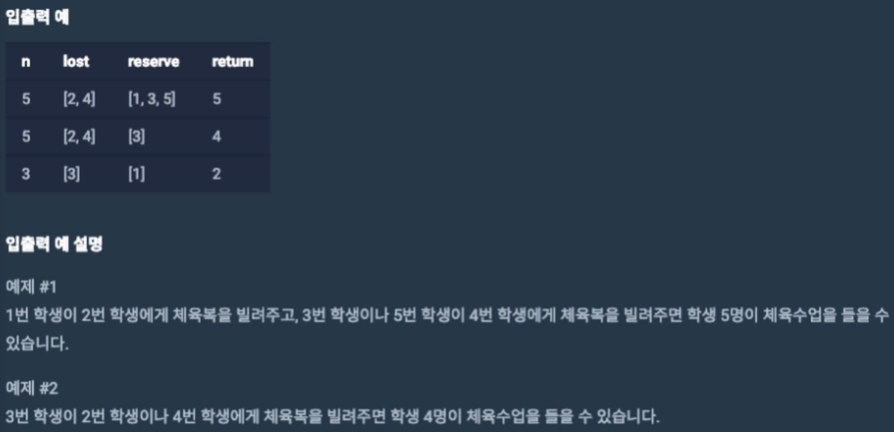
문제의 해결 - 예제

• 컴퓨터에게 문제해결을 시킬 떄는 단계별로 차례차례 시켜야 함. (단계의 흐름을 구성)
  

1번 -> 2번에게 빌려주고, 3번 -> 4번에게 빌려주는 식으로 종료함.
답은 answer = 5

빌려주는 모양을 다르게 하면,

뒤에서 빌려주는 모양으로 완성시킬 수 있다.

이 과정을 절차적으로 기술하는 것이 이번 알고리즘

탐욕법 (Greedy Algorithm)

• 그 순간에 지역적으로 최적이라고 생각되는 것을 선택
• 완전 최적은 아니지만,
  
  지금의 선택이 끝의 선택에도 좋음. 이때는 탐욕법으로 최적해를 찾을 수 있다.
• 이를 어떻게 구분해낼까?

예를 들어 누락되는 경우가 있지 않을까?

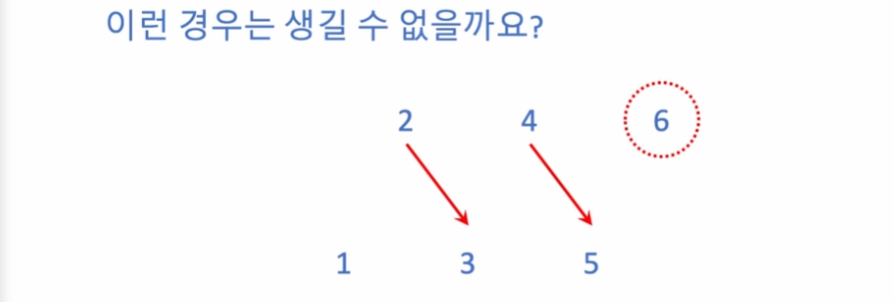
전체가 들을 수 있었는데, 못 들은 경우

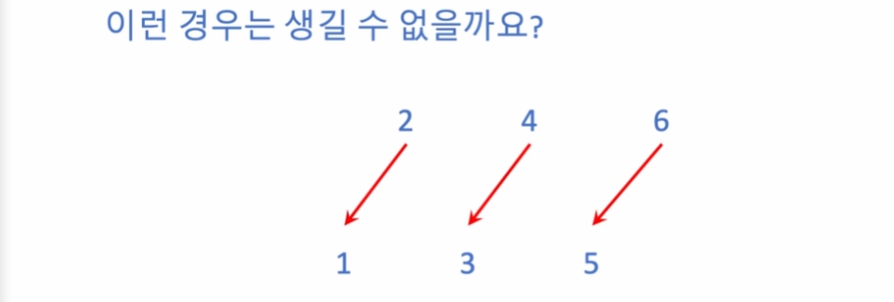
큰 번호부터 빌려주었다면, 최적해를 구할 수 있다.

학생을 "정해진 순서" 로 살피고, "정해진 순서"로 우선하여 빌려줄 방향을 정해야 함.

문제의 해결 - 방법 (1)

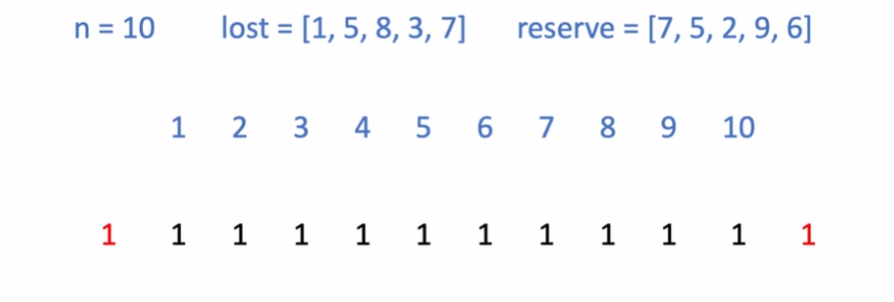
• 처음엔 모든 학생이 체육복 (1) 을 가져왔다고 가정

• 나보다 앞, 뒤 번호를 살펴봐야하니까, 0번, [모든 학생] 인덱스를 구현하여 막아놓음.

• reserve[]를 살펴봄
  

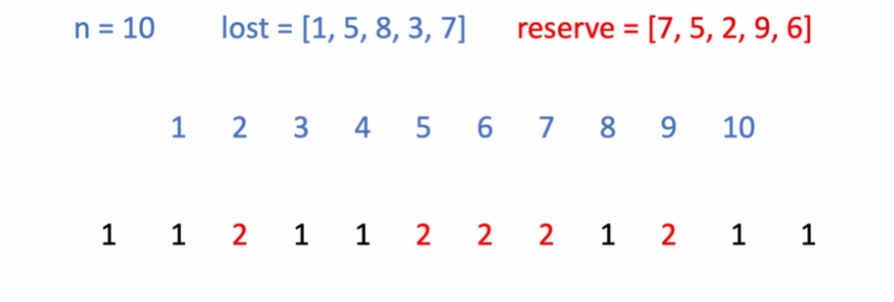
• 반영함

• lost[]를 살펴봄
  

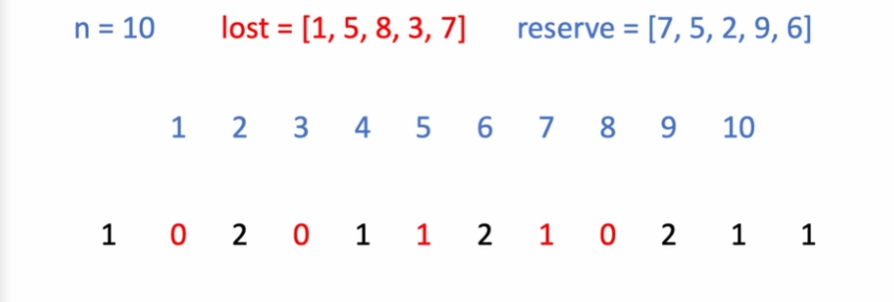
• 왼쪽부터 스캔함
  

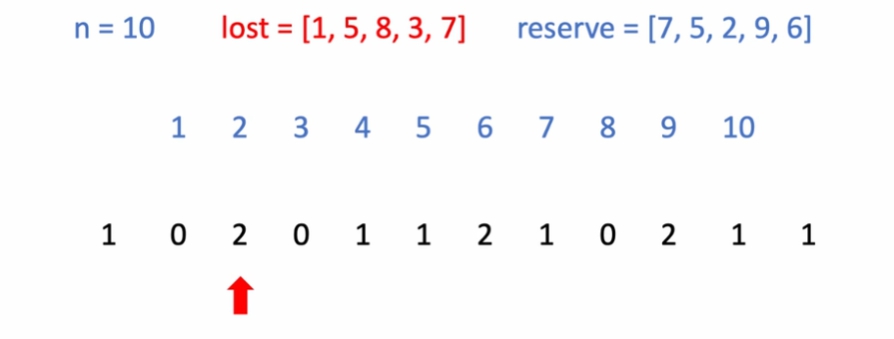
• 2번을 보았더니 빌려줄 수 있음. "번호가 작은 쪽" 부터 살펴나갔기 때문에, "번호가 작은 쪽" 방향으로 우선하여 빌려주어야 함. 안그러면 누락될 수 있음.
  
  

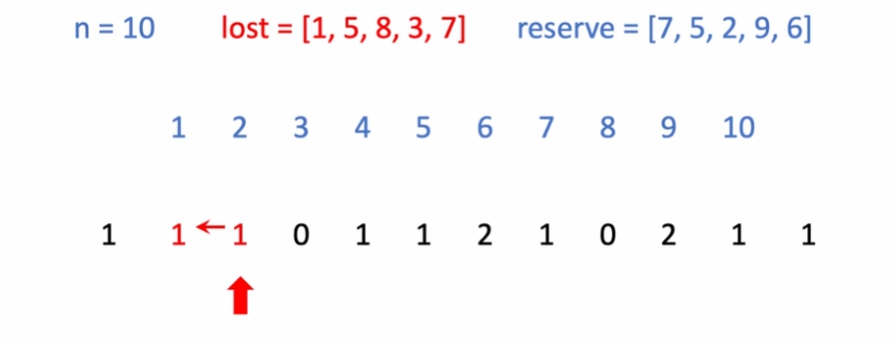
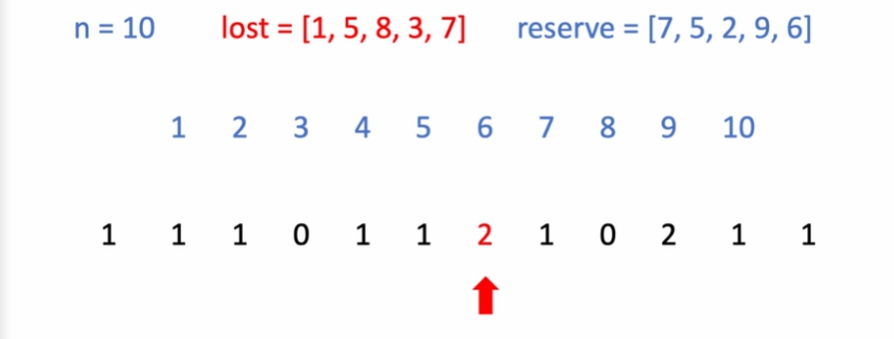
• 빌려줄 수 있으나, 주변 학생이 다 체육복이 있음.
  
  
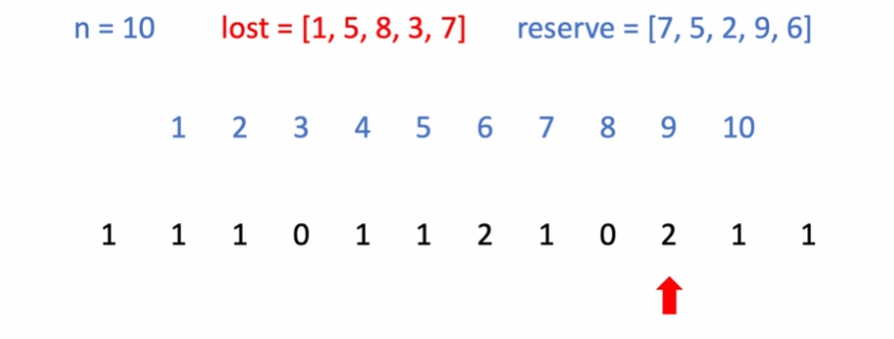
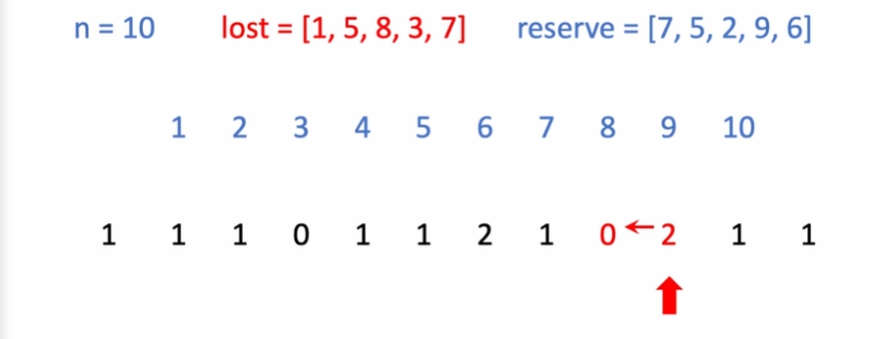
  왼쪽 8번에게 빌려줌.

• 최종적 으로 1벌 이상 갖고 있는 학생을 셈.
  

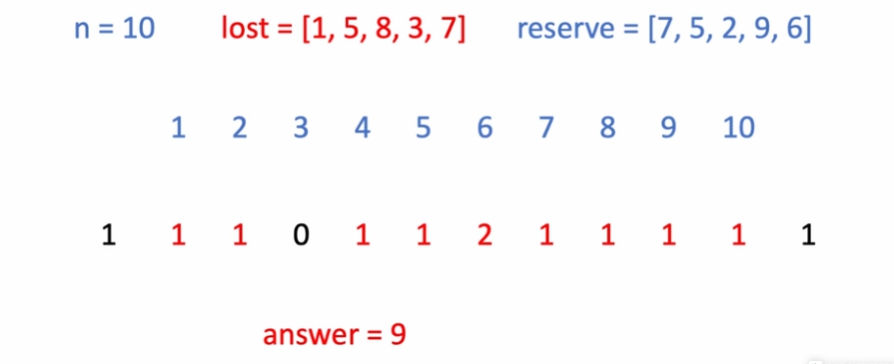
• 정답 산출

알고리즘의 복잡도

• 꽤 괜찮은 알고리즘임을 알 수 있다.

• 전체 학생수는 매우 크고 (1천만명), 여벌 체육복 가져온 학생이 매우 적다면? 실행 시간은 1천만명을 여러번 봐야하게 됨.

• 보통 여벌의 체육복을 가져온 학생이 적으니, 이걸 순서대로 살펴보고, 빌려 줄 수 있는 경우에만 처리를 한다. (전체를 볼 필요가 없음)

O(klogk)라고 해도 여벌 가져온 학생 수가 적게 되면 이 방법이 나을 수 있음.

• 다른 케이스로
• 여벌의 체육복을 가져온 학생이 매우 많고,
• 도난당한 학생이 적을 경우가 있음

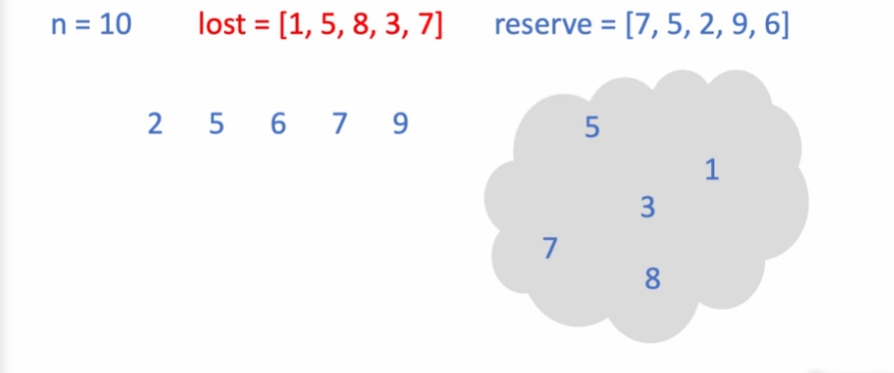
reserve를 정렬,
lost는 정렬되지 않은 해시 테이블

• 5, 7은 여벌, 도난이 동시 -> 빼냄

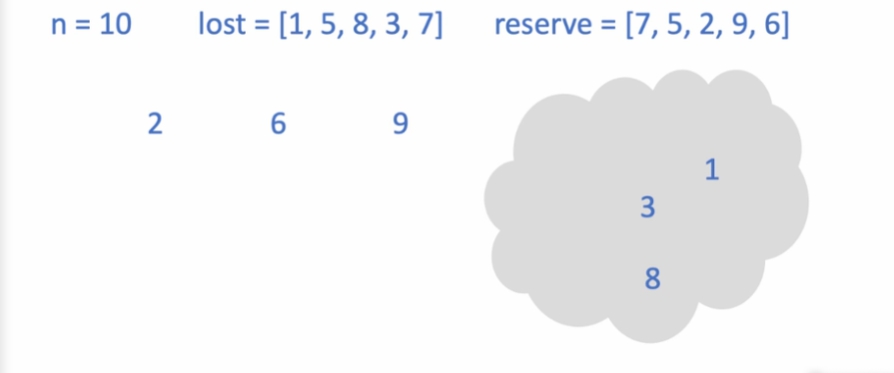
• 2번을 살펴 볼 때, 1번에게 빌려줄 수 있는 상황
  
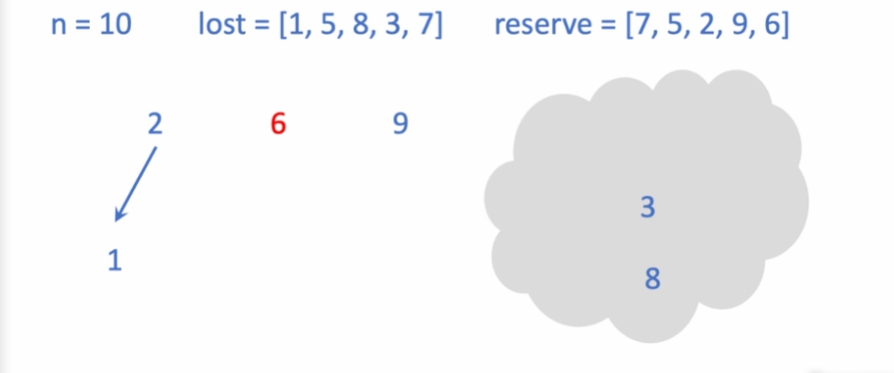
  목록에서 빼냄

6번은 5 -> 7번 순으로 확인 하고 없음. 넘어감.

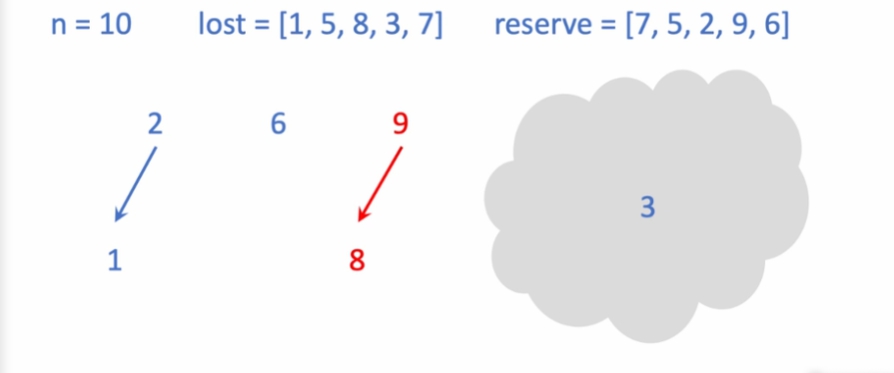
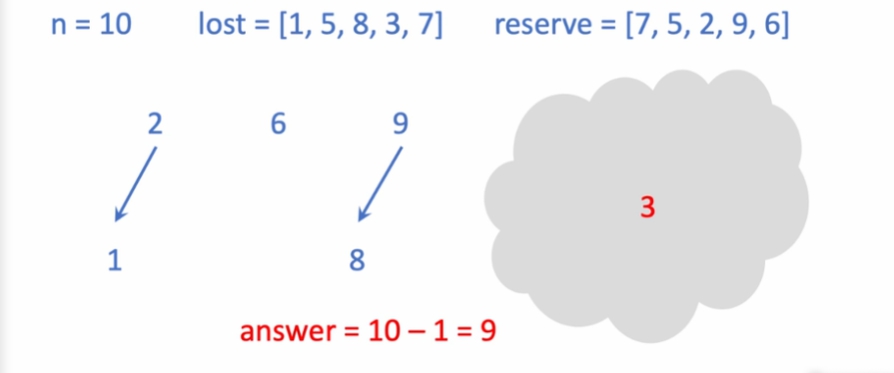
전체에서 - 빌리지 못한 학생 = 정답 을 도출함.

알고리즘 복잡도

• 여벌 체육복 가져온 학생의 정렬은 O(klogk)
• 체육복을 빌려줄 수 있는 학생
• 빌려줄 수 있는 학생 * (앞번호, 뒷번호인지 확인 -> 해시 테이블 이용)
  전체 O(klogk)
  -> n은 매우 크지만, k가 매우 작은 경우