SVM (Support Vector Machine)

Hyperplane

• p차원에서 hyperplane은 p-1차원에서의 평평한 어핀 공간(2차원-> 직선, 3차원 -> 면)
• $b+ w_1X_1 + w_2X_2 + ... + w_pX_p = b + <w,x> = 0$
• $w = (w_1, w_2, ..., w_p)$의 normal vector는 hyperplane과 orthogonal(수직) 방향을 의미
  
  
• hyperplane 위의 점 : $f(a,b) = 0$
• 점과 선 사이의 거리 : $\frac{|0.8*a + 0.6*b -6|}{\sqrt{0.8^2+0.6^2}}$
• 한쪽 : $f(a,b) < 0$, 다른쪽 : $f(a,b) > 0$

Separating Hyperplane

• $f(X) = b+ w_1X_1 +w_2X_2+...+w_pX_p$
• $f(X) > 0$인 점들과 $f(X)<0$인 점들을 분류
• $Y_i*f(X_i) > 0$ for all i
• $f(X) = 0$은 separating hyperplane을 의미

Maximal Margin Classifier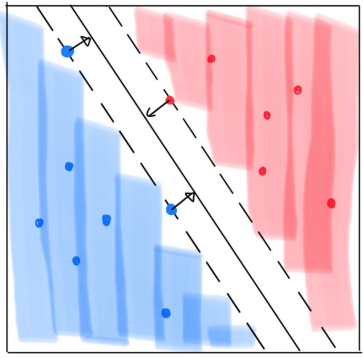

• 모든 Separating hyperplane중에서, 이진 클래스 사이의 gap 또는 margin을 최대로 만들어주는 것을 찾음

• 결정 경계에 영향을 미치는 샘플들을 서포트 벡터(support vector)라고 부름

• max M(Margine)

• $b,w_1,...,w_p$ 최적화를 통해서 최대 마진을 가지는 결정 경계 찾기

• 모든 데이터에 대한 각각의 마진은 결정된 max M보다 크거나 같다.

• subject to $\frac{y_i(b+w_1x_{i1}+...+w_px_{ip})}{||w||} \geq M$ for all $i = 1, ..., N$

• subject to $y_i(b+w_1x_{i1}+...+w_px_{ip}) \geq \hat M = M||w||$

• $max_{w,b}\frac{\hat M}{||w||}$

• $||w||$를 이용해서 $\hat M$크기를 control 가능하므로 $\hat M$의 크기 중요성이 떨어짐

• $max_{w,b}\frac{1}{||w||}$로 표현 가능

• subject to $y_i(b+w_1x_{i1}+...+w_px_{ip}) \geq 1$

• $max_{w,b}\frac{1}{||w||}$ = $min_{w,b}||w||$로 표현 가능

• $min_{w,b}\frac{||w||^2}{2}$ --> 수학적으로 계산(미분)의 편리성을 위해서 제곱후 2로 나눠준 형태로 변형

• $min_{w,b}\frac{||w||^2}{2}$ = $min_{w,b}\frac{w_1^2+w_2^2+...+w_p^2}{2}$

라그랑주 승수법(lagrange multiplier method)

• 제약식이 있는 최적화 문제를 라그랑주 승수 항을 추가해, 제약이 없는 문제로 바꾸는 방법
• 원초 문제(primal problem)
  • $min_xc^Tx$, subject to $Ax=b,Gx \leq h$
• 라그랑주 승수 벡터 $u$와 $v \geq 0$를 도입해 라그랑주 함수 $L$을 만듦
  • $L(x,u,v) = c^Tx = u^T(Ax-b)+v^T(Gx-h) \leq c^Tx$
• $f^* \geq min_xL(x,u,v) = min_xc^Tx + u^T(Ax-b) + v^T(Gx-h) = g(u,v)$
• $g(u,v)$를 라그랑지 듀얼 함수라고 부름
• 편미분의 결과가 0이 되는 지점에서 최소값을 가짐
• $\frac{\partial L}{\partial x} = c^T + u^TA + v^TG = 0$
• $c = -A^Tu-G^Tv$로 대입 및 전개
• $L(x,u,v) = -u^Tb-v^Th = g(u,v)$ --> u와 v만을 이용하여 식을 표현

Duality gap

• $f^* \geq min_xL(x,u,v) = g(u,v)$
• $g(u,v)$를 최대화하는 것은 $f^*$과 가까워지는 것
• 둘 사이의 gap을 통해서 표현
• 둘 사이의 gap이 존재하면 weak dual, 존재하지 않으면 strong dual($f^* = g(u,v)$)

라그랑주 듀얼 문제(lagrange dual problem)

• 최소화 문제를 최대화 문제로 바꾸어 풂
• $max_{u,v}-u^Tb-v^Th$
• subject to $-A^Tu-G^Tv = c, v\geq 0$

Slater's condition

• $min_xf(x)$
• subject to $h_i(x) \leq 0, i = 1, ...m$
• ------------$I_j(x) = 0, j = 1, ..., r$
• 조건 1: Primal problem이 convex
• 조건 2: There exists at least one strictly feasible $x \in R^n$
• 조건 1과 2를 만족하면 strong duality를 만족함

KKT Condition

• strong duality의 문제(Slater's condition 만족)에서는 다음의 명제를 만족함
• $x^* and u^*, v^*$ are primal and dual solutions
  $\leftrightarrow$ $x^*$and $u^*,v^*$ satisfy the KKT conditions
• 1. Stationarity 조건:
     0 $\in \partial_x(f(x) + \sum^r_{j=1}v_jl_j(x))$ ==> $L(x,u,v)$
• 2. Complementary slackness 조건:
     $u_i \cdot h_i(x) = 0$ for all i
     ll

Maximal Margin Classifier

• $min_{w,b}\frac{||w||^2}{2}$
• subject to $y_i(b+w_1x_{i1}+...+w_px_{ip}\geq 1$
  for all i =1,..., N

Dual form

• $max_{\alpha}min_{w,b}L(w,b,\alpha)$ = $max_amin_{w,b}\frac{||w||^2}{2} -\sum^N_{i=1}\alpha_i(y_i(w \cdot x_i+b)-1)$
  subject to $\alpha_i \geq0, i=1,...,N$
• By Stationary condition (in KKT condition),
  $\frac{\partial L(w,b,{\alpha_i})}{\partial w} = 0$, $\frac{\partial L(w,b,{\alpha_i})}{\partial b}= 0$
• 따라서, $w=\sum^N_{i=1} \alpha_iy_ix_i = 0$, $\sum^N_{i=1} \alpha_iy_i= 0$
• $max_\alpha \sum^N_{i=1}\alpha_i - \frac{1}{2}\sum^N_{i=1}\sum^N_{j=1}\alpha_i\alpha_jy_iy_jx_i^Tx_j$
  subject to $\alpha_i \geq0, \sum^N_{i=1}\alpha_iy_i=0$ for i = 1...N
• KKT 조건의 Complementary slackness condition에 의하면
  $\alpha_i 또는 y_i(w^Tx_i+b)-1$ 둘 중 하나는 반드시 0 --> $y_i(f(x)) = 1$-->$f(x) = y_i$
• 결정 경계에 영향을 미치는 관측치들은 오직 support vector뿐
• 그래서 서포트 벡터 머신(support vector machine)이라 부름
• $\alpha$값을 옵티마이즈 하려고 하는데 support 벡터가 아닐때는 $\alpha$가 0이 되어 영향 X
• Maximal Margin Classifier를 해결할때, Dual form으로 $\alpha$를 구하고, 2차계획법으로 w와 b를 구해 경계선 구함

Soft Margin Machine

• 선형 경계로는 완벽히 나눌 수 없는 경우 또는 noisy샘플 때문에 비효율적인 경계가 형성되는 경우
• Slack variable $\epsilon_i$를 도입해 해결
• $min_{w,b,\epsilon}\frac{||w||^2}{2}+C\sum^N_{i=1}\epsilon_i$
  subject to $y_i(b+wx_i)\geq1-\epsilon_i, \epsilon_i \geq 0$
  for all i = 1,...,N
• $max_{\alpha,\beta}min_{w,b,\epsilon}\frac{||w||^2}{2}+C\sum^N_{i=1}\epsilon_i-\sum^N_{i=1}\alpha_i(y_i(w \cdot x_i+b)-1+\epsilon_i)- \sum^N_{i=1}\beta_i\epsilon_i$
  subject to $\alpha_i \geq 0, \beta_i \geq 0$ for all i =1, ..., N
  By stationary condition(in KKT condition),
• $\frac{\partial L}{\partial w} = 0$, $\frac{\partial L}{\partial b} = 0$, $\frac{\partial L}{\partial \epsilon_i} = 0$
• 따라서, $w = \sum^N_{i=1}\alpha_iy_ix_i,\sum^N_{i=1}\alpha_iy_i=0,\alpha_i = C - \beta_i$

Hyperparameter C in SVM

• C의 값이 커지면
• 1. $\epsilon$의 영향이 커져 0으로 보내며, 마진의 폭이 줄어듬
• 2. Support vector 수가 줄어들어, 적은 샘플로 결정 경계를 찾음 --> 오버피팅 이슈 가능성
• 3. Bias $\downarrow$, Variance $\uparrow$
• C의 값이 작아지면
• 1. $\epsilon$의 영향이 작아져 마진의 폭이 커짐
• 2. Support vector 수가 늘어나, 많은 샘플로 결정 경계를 찾음 --> 언더피팅 이슈 가능성
• 3. Bias $\uparrow$, Variance $\downarrow$

Classification for SVM

• 지금까지 주어진 데이터로 결정 경계 hyperplane을 찾는 과정
• $f(x) =W^TX+b = \sum_{i\in S}\alpha_iy_ix_i^Tx+b$ --> 서포트 벡터일때만 $\alpha$가 0이 아니므로 계산량 $\downarrow$
• 예측값이 0보다 크면 $\hat y=1$로 0보다 작으면 $\hat y=-1$로 분류
• Support vector만 사용되기 때문에 연산량이 많지 않음

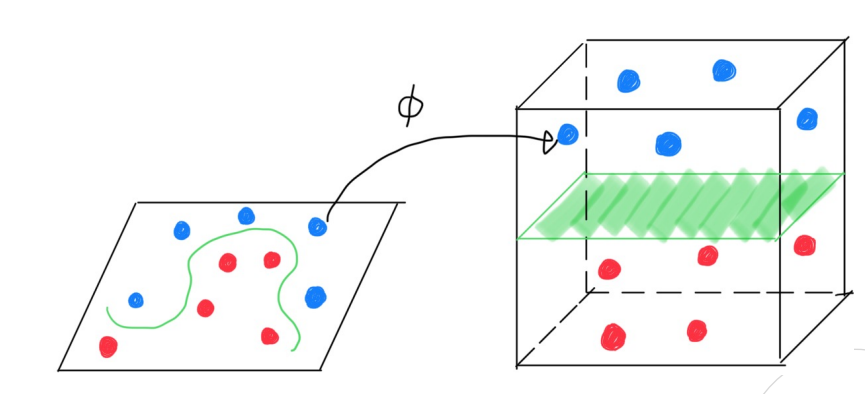
Nonlinear SVM

• Mapping function
  • 비선형 구조의 데이터를 높은 차원으로 이동시켜 그 공간에서 분류하고자 함
  • Input space에 존재하는 데이터를 feature space로 옮겨주는 mappin$(\varnothing)$
    
• Mercer's Theorem
• 1. $K(x_i,x_i)$의 경우 항상 0이상의 값을 지님
• 2. $K(x_i,x_j) =K(x_j,x_i)$(대칭 행렬 조건)
     커널 함수는 두 조건을 만족시켜야함

Kernel trick

• 조건을 만족하는 임의의 함수를 모두 커널 함수로 사용
• Linear : $K(x_i, x_j) = x^T_ix_j$
• Polynomial : $K(x_i, x_j) = (x^T_ix_j+c)^d$
• Gaussian : $K(x_i,x_j) = exp{\frac{-||x_i-x_j||^2_2}{2\sigma^2}}$
• Radial : $exp(-\gamma\sum^p_{k=1}(x_{ik}-x_{jk})^2)$

SVM with kernel trick

• $max_\alpha \sum^N_{i=1}\alpha_i - \frac{1}{2}\sum^N_{i=1}\sum^N_{j=1}\alpha_i\alpha_jy_iy_jx_i^Tx_j$
  --> $max_\alpha \sum^N_{i=1}\alpha_i - \frac{1}{2}\sum^N_{i=1}\sum^N_{j=1}\alpha_i\alpha_jy_iy_jK(x_i,x_j)$

• $w = \sum^N_{i=1}\alpha_iy_ix_i,\sum^N_{i=1}\alpha_iy_i=0,\alpha_i = C - \beta_i$
  --> $w = \sum^N_{i=1}\alpha_iy_i\varnothing(x_i),b = \frac{1}{N_{sv}}\sum^{N_sv}_{i=1}(y_i - \sum^{N_sv}_{i=1}\alpha_jy_jK(x_i,x_j))$

• 분류시 커널 함수가 사용되므로, mapping function에 대한 정의가 필요 없음
  $f(\varnothing(x)) = w^T\varnothing(x)+b = \sum_{i\in S}\alpha_iy_i\varnothing(x_i)^T\varnothing(x)+b = \sum_{i \in S}\alpha_iy_iK(x_i,x)+b$

Multiclass SVM

SVM for multiclass

• OVA(One versus All)
  • K개의 2-Class SVM을 학습하며 각자의 class와 나머지 클래스로 나눔
  • $\hat f_k(x)$의 값이 가장 큰 클래스로 분류
• OVO(One versus One):
  $K \choose 2$개의 pairwise classifier($\hat f_kl(x))$를 학습
  Pairwise competition을 가장 많이 이긴 클래스로 분류
  

SVM vs Logistic Regression

• 클래스가 거의 separable하면, SVM > LR
  아닐 경우, LR(with ridge penalty) == SVM --> LR과 L2 정규화 손실함수를 같이 썼을때 성능 같다.
• 확률값을 측정하고 싶으면, LR을 사용
• Nonlinear boundary에는, kernel SVM이 계산적인 면에서 더 좋음