1-2 기초수학
Regression vs Classification
회귀(Regression)
- 입력값 : 연속값(실수형), 이산값(범주형) 등 모두 가능
- 출력값 : 연속값(실수형)
- 모델 형태: 일반적인 함수 형태 (ex. y = wx+b)
분류 (Classification)
- 입력값 : 연속값(실수형), 이산값(범주형) 등 모두 가능
- 출력값 : 이산값(범주형)
- 모델 형태 :
- 이진 분류라면 sigmoid 함수

- 다중 분류라면 softmax 함수
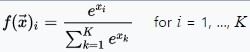
- 이진 분류라면 sigmoid 함수
Notations 용어 설명

데이터의 구성
-
데이터는 feature(독립 변수)와 label(종속 변수)로 구성
-
Feature
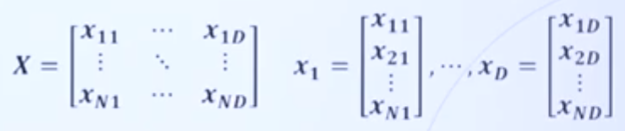
- 데이터 X의 특징, 혹은 항목을 의미
- N : epdlxj toavmf rottn, D: 피처의 갯수
- ex) 혈압, 몸무게, 나이
-
label
- 예측하려는 값
모델
- Parameter (=weight, 파라미터, 가중치)
- 주어진 데이터(입력값) 말고, 모델이 가니고 있는 학습 가능한(learnable) 파라미터
- ex) wx+b 에서 w와 b ( x : 입력값)
- Hyperparameter ( 하이퍼 파라미터)
- 모델 학습에 있어, 인간이 정해줘야 하는 파라미터
- ex) learning rate, batch 등
- input
- 모델에 입력되는 값으로 데이터의 피처 부분(x로 표기)
- output
- 모델로부터 출력되는 예측값
- Linear regresion : 파라미터를 선형 결합식으로 표현 가능한 모델
- ex) y = w0 + w1X1 + w2X2 + ...+ WdXd
- Nonlinear regression : 선형 결합식으로 표현 불가능한 모델
- ex) log(y) = w0 + w1log(x), y = max(x,0)
Basic Math for ML
-
함수
- 두 집합 사이의 관계, 혹은 규칙
- y = f(x)의 식으로 표현, 이 때의 x는 입력값, y는 출력값
-
일차 함수
- y가 x에 대한 일차식으로 표현된 경우
- y = ax + b
- a를 기울기, b를 절편이라고 표현
-
이차 함수
- y가 x에 대한 이차식으로 표현된 경우
- y = a(x-p)**2+q
-
순간 변화율
- x의 값이 미세하게 변화했을 때, y의 변화율
- 어떤 X 값에서의 그래프와 맞닿는 접선의 기울기
-
미분
- 함수 f(x)를 미분한다는 것은 함수의 순간 변화율을 구한다는 뜻
- 또는 로 표기
-
함수의 최솟값
- 함수의 최솟값에서의 미분값(순간 변화율)은 항상 0
- 이를 바탕으로 파라미터의 최적값을 구할 수 있음
-
지수함수
- a를 밑, x를 지수라고 부름
- 한쪽은 0으로 수렴, 다른 쪽은 무한대로 발산
-
자연 상수
- 2.718....
-
시그모이드 함수 (sigmoid function)
- 이진 분류 문제를 위한 비선형 함수
- y =
-
소프트맥스 함수 (softmax function)
- 다중 분류 문제를 위한 비선형 함수
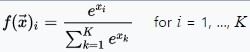
- 다중 분류 문제를 위한 비선형 함수
-
로그 함수
- 지수 함수와 역함수의 관계
- 로그 함수의 밑이 e 일 때,
Linear Regression
-
단순 선형 회귀 (simple linear regression)
- 피처의 종류가 한 개인 데이터에 대한 회귀 모델
- y =
-
다중 선형 회귀 (multiple linear regression)
- 피처의 종류가 여러 개인 데이터에 대한 회귀 모델
-
다항 회귀 (polynomial regression)
- 독립 변수(피처)의 차수를 높인 회귀 모델
Optimization을 위한 기초 수학
-
편미분
- 원하는 변수에 대해서만 미분 하는 것
- 그 외 모든 것들은 상수 취급
-
연쇄법칙 (chain rule)
-
Loss Function
- MSE
- 회귀 문제에서의 대표적인 손실 함수
- 오차의 제곱의 평균
- MSE
-
최소 제곱법(least square method)
- 최적의 파라미터를 구할 수 있는 한 방법으로, 데이터에 대한 오차를 최소화 하도록 함
- 기울기 a와 절편 b의 일차 함수
-
Gradient Descent
- 복잡한 함수의 경우 최소제곱법으로 해결 어려움
- 손실 함수의 값을 최소화시키는 방향으로 파라미터를 업데이트
- 손실 함수에 대해 미분값이 0이 되는 방향으로 파라미터의 업데이트 방향을 결정
- 슈도 코드
- 현재 파라미터에서의 손실 함수에 대한 미분값을 구함
- 미분값의 반대 방향으로 파라미터값을 업데이트
- 미분값이 0이 될 때까지 1~2번을 에폭(epoch)만큼 반복
출처 :
https://www.youtube.com/watch?v=oyzIT1g1Z3U&list=PL7SDcmtbDTTylCwjSDzGduvR-1EItFF2X
