[머신러닝] 하이퍼파라미터 튜닝 (Hyperparameter Tuning) - Bayesian Optimization

✔ Hyperparameter Tuning 의 종류

• Bayesian Optimization

  • 정의

    목적함수(loss, accuracy 등 구하고자 하는 지표)를 최대 또는 최소로 하는 최적해를 찾는 방법
    
    

  • 목표

    입력값 $x$ 를 받는 미지의 목적함수 f를 가정하여, 함숫값 $f(x)$ 를 최대로 만드는 최적해 $x^*$ 를 찾는 것이다.

    보통은, 목적 함수의 표현식을 명시적으로 알지 못함 (i.e. black-box function)
    또한, 함숫값 $f(x)$ 를 계산하는 데에 오랜 시간이 소요되는 경우를 가정

    이러한 상황에서, 가능한 적은 수의 입력값 후보들에 대해서만 함숫값을 조사하여, $f(x)$ 를 최대로 만드는 최적해 $x^*$를 찾는 것이 주요 목표이다.

  • 필수 요소

    • Surrogate Model
      현재까지 조사된 $(x_1,f(x_1)),..., (x_t, f(x_t))$ 를 바탕으로, 미지의 목적 함수의 형태에 대한 확률적인 추정을 수행하는 모델

    • Acquisition Function
      목적 함수에 대한 현재까지의 확률적 추정 결과를 바탕으로, '최적 입력값 $x^*$를 찾는 데 있어 가장 유용할만한' 다음 입력값 후보 $x_{t+1}$ 을 추천해주는 함수

  Bayesian Optimization 의 pseudo-code는 다음과 같다.

  

  • Gaussian Processes (GP)

    • Surrogate Model로 가장 많이 사용되는 확률 모델

    • 모종의 함수들에 대한 확률 분포를 나타내기 위한 확률 모델

    • 구성 요소들간의 결합 분포가 Normal distribution을 따름
      
      현재까지 조사된 $(x_1,f(x_1)),..., (x_t, f(x_t))$ 를 바탕으로, GP는 목적 함수에 대한 확률적 추정을 다음과 같이 수행한다.
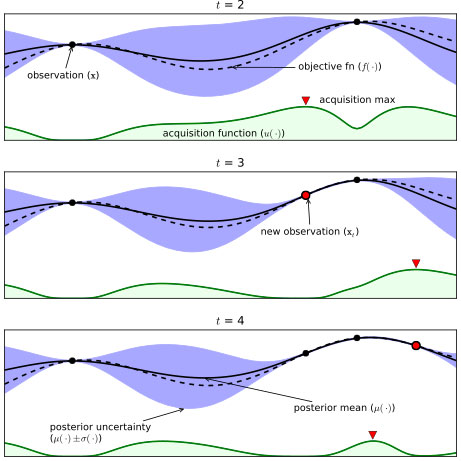      (검은색 점선 : 실제 목적 함수 , 검은색 실선 : 추정된 평균 함수 , 파란색 음영 : 추정된 표준편차 , 검은색 점 : 현재까지 조사된 입력값 - 함숫값 점 , 하단의 녹색 실선 : Acquisition Function)

    위의 그림에서 가로축을 입력값 $x$, 세로축을 함숫값 $f(x)$ 로 보면,

    • 검은색 실선 : 현재까지 조사된 점 $(x_1,f(x_1)),..., (x_t, f(x_t))$ 에 의거하여 추정된 각 $x$ 위치 별 평균 $μ(x)$

    • 파란색 음영 : 각 $x$ 위치 별 표준편차 $σ(x)$

    $μ(x)$ 의 경우, 현재까지 조사된 점 $(x_1,f(x_1)),..., (x_t, f(x_t))$ 을 반드시 지나도록 형태가 결정됨
    조사된 점에서 가까운 위치일수록 $σ(x)$ 가 작고, 멀어질수록 $σ(x)$ 가 커지는 양상임 $\rightarrow$ 이는 조사된 점으로부터 거리가 먼 $x$ 일수록, 이 지점에 대해 추정한 평균값의 불확실성이 크다는 의미를 내포함

    위의 그림에서 $t = 3, t = 4$ 로, 조사된 점의 개수가 늘어날수록, $\sigma(x)$ 의 영역의 크기가 감소한다. 이는, 조사된 점의 개수가 증가할수록 목적 함수의 추정 결과에 대한 불확실성이 감소되었다는 것을 보여준다. 또한, 그런 경향이 강해질수록 목적 함숫값을 최대로 만드는 입력값 $x^*$ 를 제대로 찾을 가능성이 높아진다.
    
    

  • Acquisition Function

    Acquisition Function 은 목적 함수의 최적 입력값 $x^*$ 를 찾는 데에 있어 가장 유용할 만한 $x_{t+1}$ 을 추천해준다. 이 때의 '유용할만한'의 의미에 대해 자세히 알아보겠다. 이를 위해, GP를 사용한 목적 함수의 확률적 추정 과정 중 $t = 2$ 때의 그림을 다시 가져왔다.
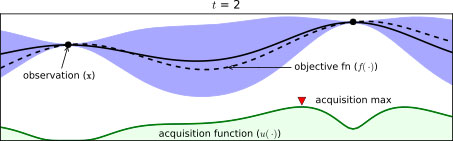    $t = 2$ 시점에서 빨간색 세모 지점에서 최댓값이 나왔다. 이 부근이 다음 시점인 $t = 3$ 에서의 관찰 지점이 되는 것이다. 이런 과정을 반복하면서 hyperparameter 조합을 최적화해나간다.
    
    

    현재까지 조사된 점은 총 2개이다. 이 중 함숫값이 더 큰 오른쪽에 위치한 점 근방에서 '실제 최적 입력값 $x^*$를 찾을 가능성이 높을 것이다' 라고 예측하는 것은 그럴싸한 예측이라 할 수 있다.
    즉, 현재까지 조사된 점들 중 함숫값이 최대인 점 근방을 다음 차례에 시도하는 것이 합리적인 전략이라고 할 수 있다. 이를 exploitation (착취) 이라고 한다.
    
    다른 관점으로 보면, 표준편차(=불확실성) $\sigma(x)$ 가 큰 영역의 경우, 이 부분의 추정된 평균 함숫값이 실제 목적 함숫값과 유사할 것이라 장담하기 매우 어려울 것이다. 따라서, '불확실한 영역에 최적 입력값 $x^*$ 가 존재할 가능성이 있으므로, 이 부분을 추가로 탐색해야한다.' 는 꽤 그럴싸한 판단이다. 이에 따라, $\sigma(x)$ 가 최대인 점 근방을 다음 차례에 시도하는 것 또한 합리적인 전략이다. 이를 exploration (탐색) 이라 한다.

    exploration 과 exploitation 모두 최적 입력값 $x^*$ 를 찾는 데에 있어 균등하게 중요하나, 서로 trade-off 관계에 있다. 따라서, exploration 과 exploitation 간의 상대적 강도를 적절하게 조절하는 것이 중요하다.
    
    

• Expected Improvement (EI)

  • 정의
    Expected Improvement (EI) 는 exploration & exploitation 전략 모두를 일정 수준 포함하도록 설계된 것으로, Acquisition Function 으로 가장 많이 사용된다.
    
    EI는 현재까지 추정된 목적 함수를 바탕으로, 임의의 후보 입력값 $x$ 에 대하여 '현재까지 조사된 점들의 함숫값 $f(x_1), ..., f(x_t)$' 중 최대 함숫값인 $f(x^+) = max_if(x_i)$ 보다 더 큰 함숫값을 도출할 확률 (Probability of Improvement, i.e. PI)' 및 '그 함숫값과 $f(x^+)$ 간의 차이값'을 종합적으로 고려하여, 해당 입력값 $x$ 의 '유용성'을 나타내는 숫자 를 출력한다. 이 때, PI의 개념을 이해하기 위해 아래 그림을 살펴보자.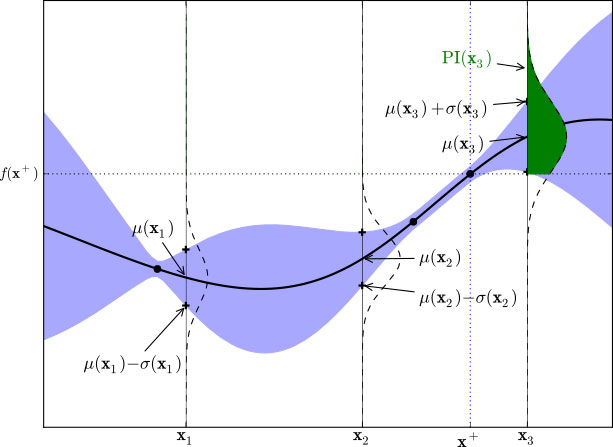

    (GP 사용 시, '최대 함숫값 $f(x^+)$ 보다 더 큰 함숫값을 도출할 확률 (PI) 에 대한 시각화 예시)
    (세로방향 점선 : 입력값 $x_1$, $x_2$, $x_3$ 에서의 함숫값 $f(x_1)$, $f(x_2)$, $f(x_3)$ 각각에 대한 확률 분포 $\rightarrow$ Normal Distribution
    초록색 음영 : $f(x_3)$ 의 확률 분포 상에서, 그 값이 $f(x^+)$ 보다 큰 영역)

    위 그림에서 현재까지 조사된 조사된 함숫값 중 최대 함숫값 $f(x^+)$ 는 맨 오른쪽에 위치한 점에서 발생한다. 이보다 더 오른쪽에 위치한 후보 입력값 $x_3$ 에 대하여, 확률적 추정 결과에 의거하여 $f(x_3)$ 의 확률 분포를 그림과 같이 기울어진 Normal Distribution 형태로 나타낼 수 있다.

    $f(x_3)$ 의 확률 분포 상에서, $f(x^+)$ 보다 큰 값에 해당하는 영역을 초록색 음영으로 나타내었다. 이 영역의 크기가 클수록, '$f(x_3)$ 이 $f(x^+)$' 보다 클 확률이 높다' 는 것을 의미한다. 이는 곧, 다음 입력값으로 $x_3$ 을 채택할 시, 기존 점들보다 더 큰 함숫값을 얻을 가능성이 높을 것이다. 따라서, 목적 함수의 최적 입력값 $x^*$ 를 찾는 데에 있어 $x_3$ 이 '가장 유용할 만한' 후보라고 판단할 수 있다.

    입력값 $x_3$ 에 대하여 계산한 PI 값에, $f(x_3)$ 에 대한 평균 $\mu(x)$ 와 $f(x^+)$ 간의 차이값인 $f(x_3) - f(x^+)$ 만큼을 가중하여, $x_3$ 에 대한 EI 값을 최종적으로 계산한다. '기존 점들보다 더 큰 함숫값을 얻을 가능성이 높은 점을 찾는 것' 도 중요하지만, '그러한 가능성이 존재한다면, 실제로 그 값이 얼마나 더 큰지' 도 중요한 고려 대상이기 때문에, 이를 반영한 계산 방식이라고 볼 수 있다.

    GP를 사용할 시의 EI 계산식을 정리하면 다음과 같다.
    
    $EI(x) \; = \; E[max(f(x) - f(x^+), 0] \\ \quad \quad \quad \\ \quad \quad \quad \; = \; \begin{cases} (\,\mu(x) - f(x^+) - \xi\,)\,\Phi(Z) + \sigma(x)\phi(Z)\,,\;if\;\sigma(x) > 0\\ \\ \quad \quad \quad \quad \quad \quad \quad \quad 0\quad \quad \quad \quad \quad \quad \quad\;,\,if\;\sigma(x) = 0\geq0 \end{cases}$

    ( $\Phi$ : 표준 정규분포의 누적분포함수 (CDF)
    $\;$ $\phi$ : 표준 정규분포의 확률분포함수 (PDF)
    $\;$ $\xi$ : exploration 과 exploitation 간의 상대적 강도를 조절해주는 파라미터이다. $\xi$ 를 크게 잡을수록 exploration 의 강도가 높아지고, 작게 잡을수록 exploitation 의 강도가 높아진다. )
    
    
    GP를 사용한 목적 함수 추정 과정의 $t = 4$ 일 때, 위의 EI 계산식을 이용하여 각 입력값 $x$ 별 $EI(x)$ 를 계산한 결과를 표시하면, 아래 그림의 하단에 있는 초록색 실선과 같이 나타난다.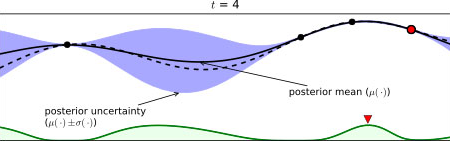

    실제로, 현재까지 조사된 점들 중 최대 함숫값을 가지는 점 $x^+$ 주변에서 EI 값이 크고 (exploitation) 그와 동시에 현재까지 추정된 목적 함수 상에서, $\sigma(x)$ 가 최대인 점 주변에서도 EI 값이 큰 (exploration) 것을 위의 그림을 통해 알 수 있다.

• 요약

  Hyperparameter Tuning 에는 Grid Search, Random Search 등이 있지만, hyperparameter 조사 과정에서 얻은 사전지식을 전혀 반영하지 못한다는 한계가 존재한다.

  Bayesian Optimization은 새로운 hyperparameter 값에 대한 조사를 수행할 시, 사전지식을 충분히 반영하면서, 전체적인 탐색 과정을 체계적으로 수행해볼 수 있다. 주로 DL보다는 ML에 사용된다.

  Bayesian Optimization의 구성 요소 중 하나인 Surrogate Model은, 현재까지 조사된 입력값-함숫값 점들을 바탕으로, 어느 미지의 목적 함수에 대한 확률적인 추정을 수행하는 모델을 지칭하며, Gaussian Process (GP) 가 대표적이다.
  

다음 포스팅에서는 Bayesian Optimization을 이용한 기법인 HyperOpt 에 대해 알아보겠다.