Recurrent Neural Networks

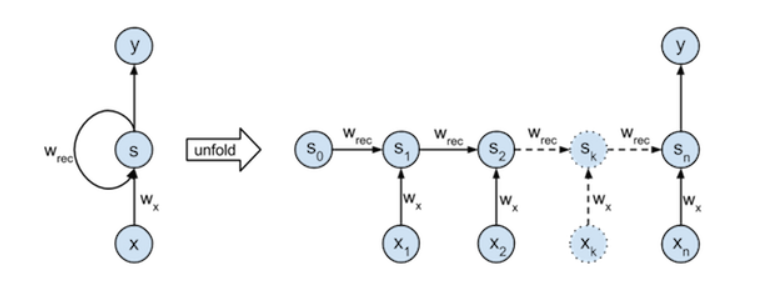
Recurrent Neural Networks (RNNs)은 가변적인 길이의 시퀀스를 다룰 수 있는 신경망의 한 종류 이다. 주된 특징은 이전 데이터가 현재 데이터에 영향을 준다는 것이다. 이러한 특징으로 인해 시간에 의존적이거나 순차적인 데이터 학습에 활용된다.

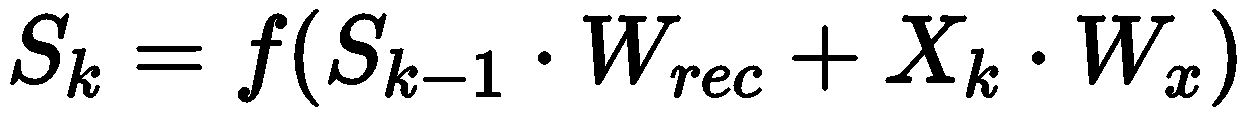
위 식은 과제에서 주어진 Linear Recurrent Neural Network 의 Feedforward 식이다. k는 각 시점을 의미하고 S는 상태, X는 Input을 나타낸다. 이번 과제는 10개의 layer를 이용하여 RNN으로 적절한 Wres와 Wx를 찾아내는 것이 목표이다.

Forward step

위에 나타난 식처럼 Wx와 Wrec를 이용하여, 현재 상태인 Sk를 알아내는 것이 목표인 단계이다. 기존의 RNN에서는 활성화 함수를 사용하지만 이번과제에서는 따로 활성화 함수를 사용하지 않았기에 Backpropagation을 구현하기 보다 수월했다.

def update_state(xk, sk, wx, wRec):
    return xk * wx + sk * wRec

def forward_states(X, wx, wRec):
    # 모든 input 시퀀스 X 들에 대한 상태를 담고 있는 행렬 S 초기화
    S = np.zeros((X.shape[0], X.shape[1]+1))
    for k in range(0, X.shape[1]):
        # S[k] = S[k-1] * wRec + X[k] * wx
        S[:,k+1
 

위 코드는 주어진 식에 맞게 짜여진 Forward step 코드이다. X의 Shape는 (100,10)으로 위에 언급한 듯이, 10개의 layer를 가지게 되고, 각 단계의 아웃풋은 S에 저장되고 최종 Output은 S[11]에 저장되게 된다. 이것을 이용해 LOSS를 구하고, Backpropagation을 구할 수 있다.

Backpropagation

이제 적절한 Wrec과 Wx를 찾기 위해 Backpropagation Step을 수행해야 한다. 이 단계를 수행하기전에 경사하강법과, Chain rule에 대해 이해 할 필요가 있다. Chain rule은 연쇄 법칙이라고도 부르며 합성함수를 미분 할때, 사용하는 공식이다. 쉽게 말하면 f(x) 함수에 들어가 있는 x가 또다른 함수 g(x)의 결과일 때 쓰는 방법이다.

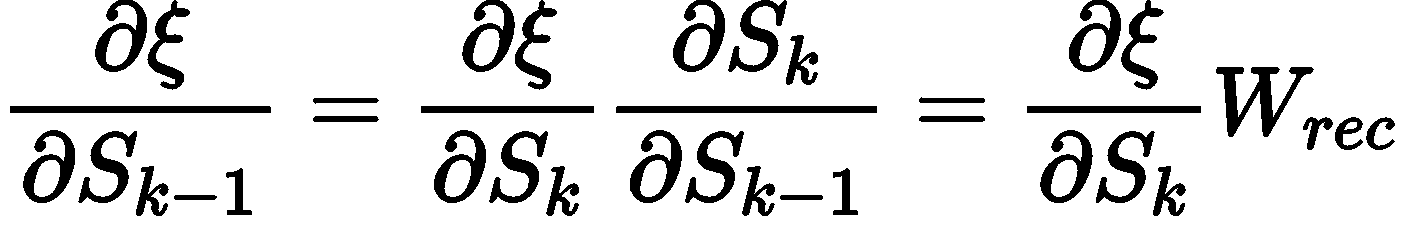
이 체인룰을 이용하여, 각 단계의 Sk의 기울기들을 알 수 있다. 이렇게 구해진 기울기를 각 단계의 Input Xk와 이전 단계인 Sk-1과 곱하면 각 단계의 Wx와 Wrec의 기울기를 알 수 있다. 이렇게 구해진 각 기울기를 러닝레이트와 곱하고 각 단계의 Wx ,Wrec 와 빼주게되면 경사하강법에 의해 최적의
Wx와 Wrec를 구할 수 있다.

 for k in range(X.shape[1],0,-1):
        wx_grad+=np.sum(np.mean(grad_over_time[:,k]*X[:,k-1],axis=0))
        wRec_grad+=np.sum(np.mean(grad_over_time[:,k]*S[:,k-1]),axis=0)
        grad_over_time[:,k-1]=grad_over_time[:,k]*wRec

위 코드는 위의 식을 코드화 한것으로 이번 과제의 역전파 구현 코드이다.