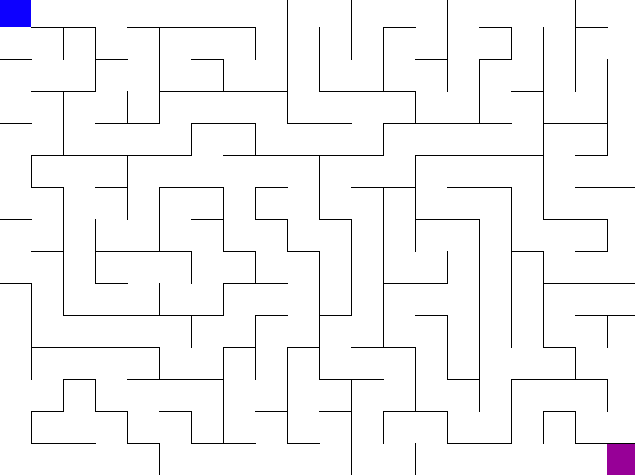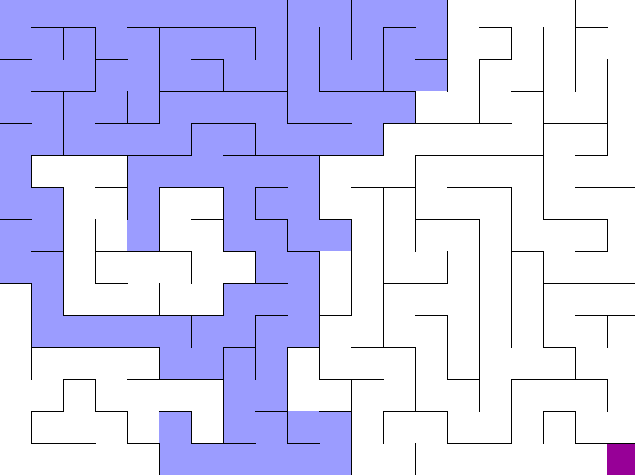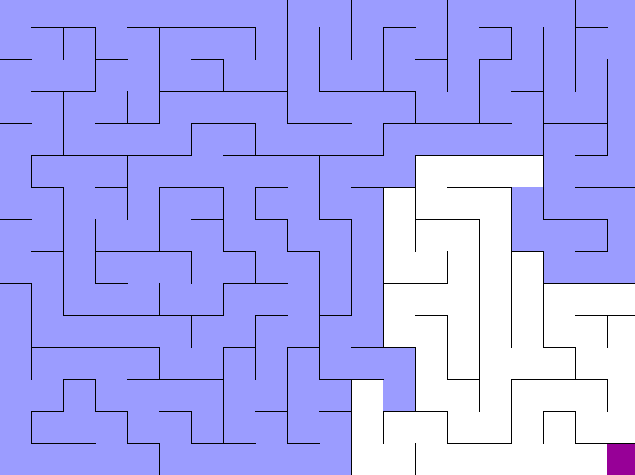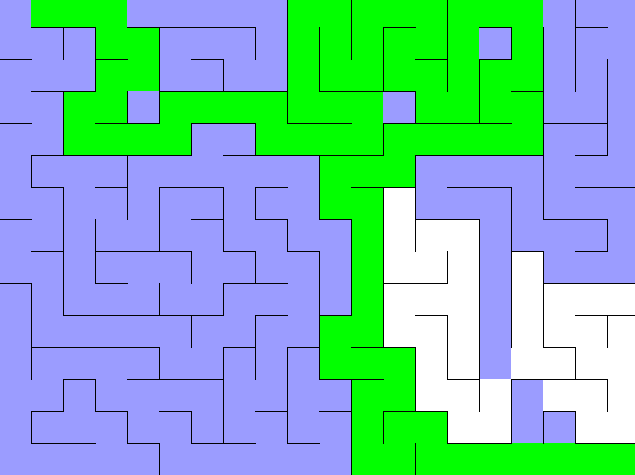
5. BFS
BFS(너비 우선 탐색 : Breadth First Search) 역시 지난 시간까지 봤던 DFS와 더불어 그래프 탐색 알고리즘이며, 길찾기 알고리즘에서 활용이 가능하다. 탐색 순서의 차이점이라면 DFS는 한 곳을 집중적으로 파고들지만 BFS는 전선에 걸쳐서 점진적으로 탐색한다.
자바로 길찾기 메소드를 구현할 때, BFS는 시작 노드를 중심으로 전선에 걸쳐서 탐색을 시작하기 때문에 별도의 추가 백트랙킹 설정 없이 최단 경로 탐색이 가능했다. 그래서 개인적으로는 DFS보다 BFS를 머릿속에서 그리며 의사코드 작성이 더 간편했다.
개념 구현은 생략한다. 이유는 DFS에서 사용하는 스택을 큐로 바꾼 것이 BFS이기 떄문. 또한, 예시로 정리할 프로그래머스 문제 의사코드에서 다룰 것은 길찾기와 관련된 문제를 바탕으로 연습을 수행할 예정.
1) 미로 길찾기
(1) 문제 확인
문제로 주어지는 미로는 이중 리스트다. 내부 리스트의 요소는 0(벽)과 1(길)로 이뤄져 있으며 시작 요소에서 도착 요소까지의 최단 거리를 리턴해야 한다. 예시를 들자면...
maze = [
[1, 0, 0, 0, 0, 0],
[1, 1, 0, 1, 1, 1],
[0, 1, 0, 1, 0, 1],
[1, 1, 1, 1, 0, 1],
[1, 0, 0, 1, 0, 1],
[1, 1, 0, 1, 1, 1]
]이런 미로를 생각할 수 있을 것이고, 시작 정점을 maze[0][0]에서 도착 정점을 maze[5][5]을 두고 그곳까지 걸릴 최단 거리를 산출하는 것이다.
(2) 상하좌우
처음 이 유형을 마주했을 때 당황했던 이유는, 단순히 값을 누적하는 식으로 탐색을 수행하는 것을 넘어서 탐색의 방향을 리스트 내에서 유동적으로 제어해야 된다는 점이었다.
제시되는 미로의 형태를 잘 파악하면, 인덱스를 좌표값으로 삼아서 요소(정점)의 위치를 특정할 수 있다. 그 말인 즉슨, 인덱스에 1씩 가산을 하면서 상하좌우 방향을 제어할 수 있다. 그것을 가능케 하는 핵심 코드가 아래와 같다.
dx = [1, -1, 0, 0] # 상하
dy = [0, 0, -1, 1] # 좌우행의 인덱스는 0부터 시작해서 하향으로 오름차순이 되는 식임을 잊지 말 것.
(3) BFS를 선택한 이유
앞서 자바에서 구현했던 길찾기 메소드에서 DFS는 백트랙킹을 신경써줘야 최단 경로를 탐색할 수 있었던 반면, BFS는 모든 전선이 동일한 순서로 탐색을 진행하기 때문에 BFS로 의사코드를 작성하고 구현하는 것이 간편했다. 그리고 그에 맞춰서 코드를 작성하는 게 훨씬 간단하기도 했고.
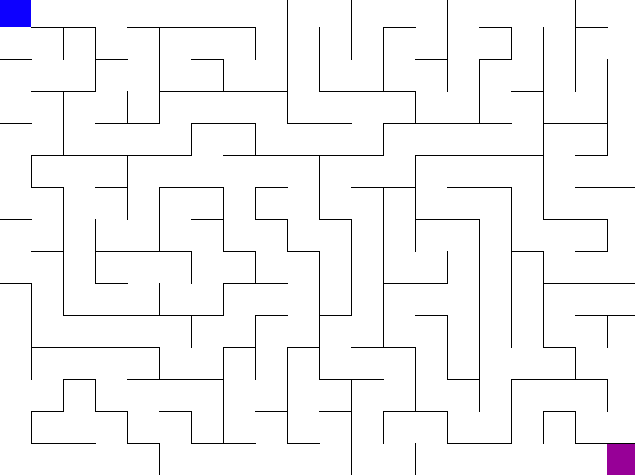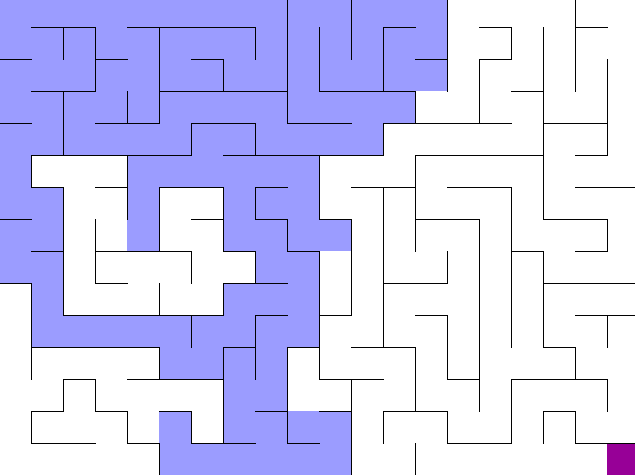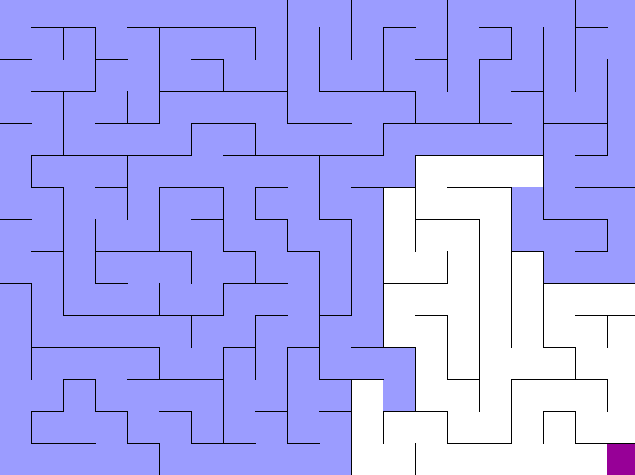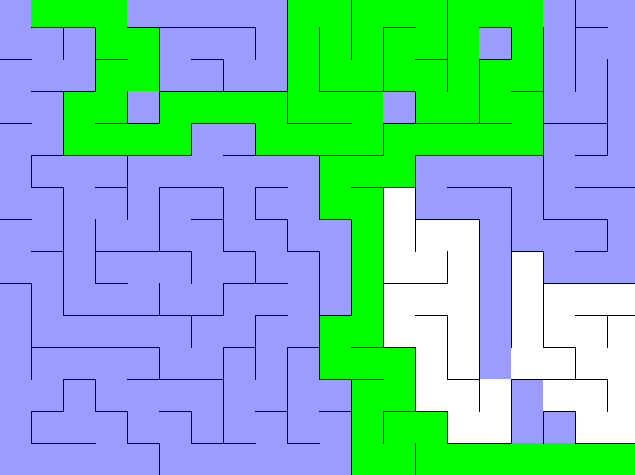
위의 그림처럼 BFS는 중간에 마주하는 갈림길을 동시에 갈라지며 탐색하게 된다. 만약 DFS였다면 갈림길에서 어차피 pop된 하나의 선택 경로로 깊숙히 들어가게 되므로 백트랙킹 조건을 잘 설정해야 갈림길에서 최단 경로를 선택하고 그 거리를 리턴할 수 있다.
요약하자면, BFS로 푸는 것이 DFS로 푸는 것보다 간단(?)해서.
(4) 문제 풀이
문제 풀이 코드는 아래를 참고할 것. 길찾기 관련 문제는 상당히 예시가 많고, 이외에도 면적 산출 등에서도 응용이 가능하므로 자주 애용하는 알고리즘이 될 것 같다(사실 DFS 적용하면서 백트랙킹에 진절머리가 나서 그렇다)
