4. DFS & 백트랙킹
지난 시간부터 이어서 멀미가 날 정도로 DFS 알고리즘 풀이를 연습했다. 다신 그래프가 보기 싫어질 정도로(...) 풀었음에도 여전히 감각의 정도로만 익혀졌고 유연하게 활용하는 건 아직도 하아아안참 남은 듯하다...
DFS를 활용할 때 단짝처럼 따라오는 것이 백트랙킹이었다. 백트랙킹은 탐색의 제약이며, 제약이 존재하지 않으면 탐색은 막장에 다다를 때까지 계속해서 이뤄진다. 이는 필연적으로 메모리 낭비와 시간 소모로 이어진다. 그래서 DFS를 사용할 때는 백트랙킹을 적재적소에 잘 활용해야 되는데... 는 무슨 DFS도 여전히 어려워요 BFS는 이러다 까먹겠어요🥲
백트랙킹과 관련해서 대표적인 문제가 n-Queen 문제다. n * n 체스보드의 격자 단위를 탐색하면서 기물 퀸이 공격 위협을 받지 않으면서 놓여질 수 있는 위치를 찾는 문제인데, 이 문제의 풀이를 정리하면서 DFS와 백트랙킹 문제 풀이에서의 2% 부족했던 감각(?)을 깨우칠 예정.
2) n-Queen
(1) 문제 조건
- 체스보드의 크기는
n * n크기의 정사각형이다.- 기물 퀸은 상하좌우 + 대각선으로 움직인다.
- 서로를 위협하지 않도록 놓을 수 있는 위치를 탐색한다.
- 배치되는 퀸의 개수는 n개다.
사실 처음 문제를 봤을 때 어떻게 풀어야 하는가...(진심) 하면서 봤었다. 체스의 규칙은 이미 알고 있어서, 문제 조건을 이해하는 것은 그리 크게 어렵지 않았다. 풀이가 벙쪄서 그렇지.
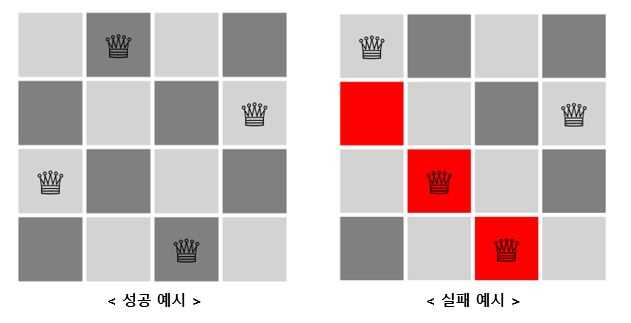 만약
만약 4 * 4 체스보드를 기준으로 생각하면 위처럼 풀이 과정이 진행될 것이다.
(2) DFS 적용 : 시작 노드
문제 풀이에 앞서, 퀸 기물의 이동 특징이 상하좌우 + 대각선이었다. 대각선 움직임은 잠시 뒤로 미루고, 상하좌우 움직임에 먼저 집중하자. 사실 상하좌우 움직임은 표현에 좀 더 치중한 것이고 이걸 조금 더 컴퓨터스럽게(?) 나타내자면 행과 열이라는 개념으로 나타낼 수 있겠다.
즉, 퀸을 배치하는 데에 있어서 두 개 이상의 퀸이 동일 행 혹은 동일 열에 존재하면 안 된다라는 전제조건을 쉽게 생각할 수 있다. 또한, 결국 풀이에 DFS를 적용하면서 동시에 백트랙킹 조건을 설정하는 것이 필요하므로 백트랙킹 조건이 곧 퀸의 배치 규칙이 된다.
앞서 행과 열이라는 표현을 쓴 이유는, 결국 체스보드 위의 격자 단위가 곧 퀸이 배치될 곳임과 동시에 움직이는 장소이기도 하다. 즉, 그래프에서의 노드가 될 수 있다. 그리고 격자 단위로 배치된 노드이기 때문에 배열을 활용해서 손쉽게 표현할 수 있다. 가령 간단하게 2 * 2 체스보드라면...
# 2 * 2
chess_board = [
[0, 0],
[0, 0]
]이런 식으로 중첩 배열의 표현이 가능해지며, 내부 배열의 요소가 곧 노드의 위치를 나타내며 이것을 인덱스로 추적할 수 있다. 예를 들어 좌상의 격자는 chess_board[0][1]로 표현할 수 있을 것이다. 또한 체스보드의 동일 행과 열에 2개 이상의 퀸을 배치할 수 없으므로 머릿속으로 그리기 쉽게 상단 1행을 DFS 시작 노드로 생각한다. 왜냐하면 행에는 1개의 퀸만 올 수 있기 때문이다.
(3) DFS 적용 : 탐색 방법
상단 1행이 곧 시작 노드의 위치가 되므로, 동시에 상단 1행에 퀸 2개를 배치해서 탐색을 시작할 필요가 없다. 이제 남은 고려사항은 동일 열과 대각선이다.
임의의 단위 격자를 chess_board[i][j]로 표현할 수 있을 것이다. 읽고 적용하는 기준에 따라서 실물 체스보드의 좌표와 중첩 배열에서의 좌표 대치가 달라지겠지만 나는 읽기 쉽게 중첩 배열(위의 코드)에서 보이는 내용 그대로 실물 체스보드에 적용시킨다.
i는 행을 나타내고 j는 열을 나타나게 된다. 두 개의 퀸의 좌표를 확인했을 때, i 또는 j가 같은 값을 가지면, 그것은 같은 행 혹은 같은 열에 위치한다는 뜻이므로 둘 중 하나라도 같은 값을 가지는 퀸의 좌표는 배치되어서는 안 되는 좌표를 의미한다고 볼 수 있겠다. 이로써 행과 열에 대한 배제 방법을 마련하였다.
다음으로 대각선에 대한 배제 방법을 마련해야 한다. 행과 열만을 나타내는 i와 j를 통해 대각선 정보를 어떻게 표현할 수 있나 고민하다가 절댓값을 적용하면 되겠다는 생각이 들었다.
chess_board = [
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 2, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1],
]위의 중첩 배열에서 1 두 개와 2 두개는 각각 서로 대각선 위치에 존재한다. 저 네 개의 좌표를 i와 j로 표현해보고, 행의 좌표끼리의 차이와 열의 좌표끼리의 차이의 절댓값을 비교한다.
first_one = chess_board[1][1]
second_one = chess_board[8][8]
# 행의 좌표끼리의 차이 = -7
# 열의 좌표끼리의 차이 = -7
first_two = chess_board[3][6]
second_two = chess_board[5][4]
# 행의 좌표끼리의 차이 = -2
# 열의 좌표끼리의 차이 = 2대각선 관계에 위치한 두 좌표의 특징은 행의 좌표끼리의 차이의 절댓값과 열의 좌표끼리의 차이의 절댓값이 같음을 알 수 있다. 이를 통해 탐색 가능한 노드, 즉 좌표를 선택할 수 있는 로직을 구상할 수 있다.
(4) DFS 적용 : 백트랙킹 조건
백트랙킹 조건은 매우 간단하다. 만약 아래와 같은 상황을 가정해보자.
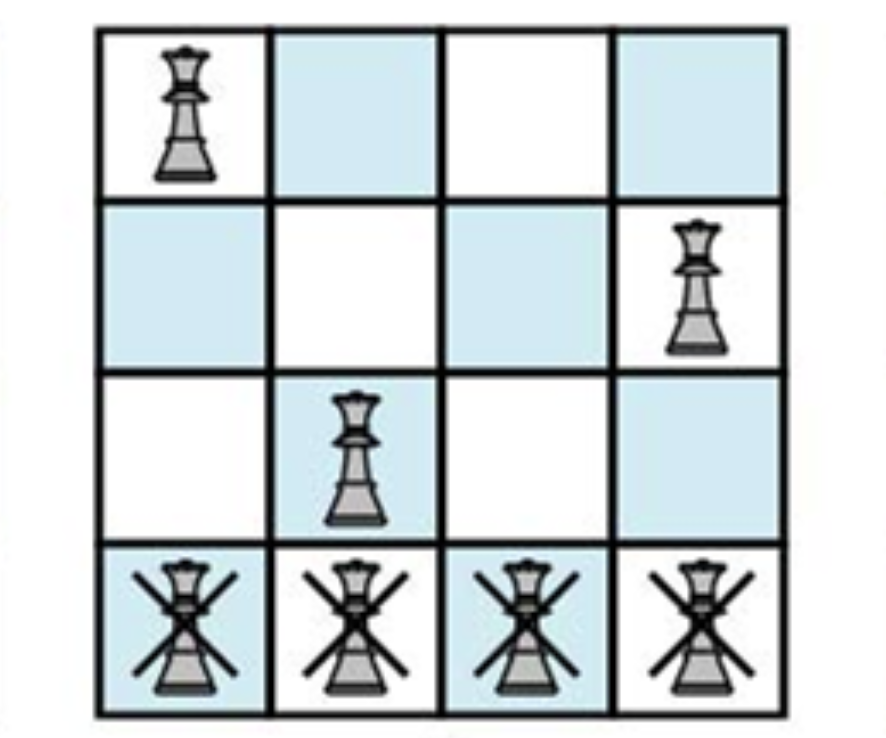
어찌어찌 3행까지의 탐색을 완료하고 다음 4행을 탐색해야 한다. 그런데 4행을 탐색하면 더 이상 행, 열, 대각선이 겹치지 않는 좌표가 존재하지 않는다. 즉, 더 이상 퀸을 배치할 수 없기 때문에 chess_board[0][0] - chess_board[1][4] - chess_board[2][2]로 연결되는 그래프를 더 탐색할 필요가 없다.
즉, 직전 노드인 chess_board[2][2]가 아닌 다음 단계의 노드, chess_board[2][3]으로 넘어가서 연이어 탐색하면 된다. 이렇게 더 이상 배치 가능한 좌표가 존재하지 않는 행이라면 굳이 그 너머를 탐색할 필요가 없다. 어차피 단위 행에는 단 1개의 퀸만 배치될 수 있는데 행에 배치할 수 없는 퀸이 나타났다면 그건 이미 n개를 배치할 수 없는 것과 마찬가지이기 떄문이다.
(5) 의사코드 작성
우선, 최상단 행의 단위 격자마다 시작 노드로 삼을 것이므로 시작 노드를 설정해서 탐색을 수행하는 로직을 총 n번 수행하면 될 것이다.
초기에는 DFS용 스택에 좌표 경로 리스트 목적의 빈 리스트를 넣어주고 리스트의 길이를 행의 좌표로 삼는다. 좌표 경로 리스트에는 탐색에서 지속적으로 변하는 요소를 감안해서 리스트로 행과 열 좌표를 입력해서 잇는다.
stack = [] # DFS용 스택
path = [] # 좌표 리스트 담기 위한 경로 리스트
result = [] # 모든 경로를 담기 위한 정답 리스트
for i in range(n):
stack.append([[0, i]]) # 초기 경로 및 시작 좌표 세팅
while stack:
# 탐색 시작
# 백트랙킹
# 기타 등등...while문 내부에서의 탐색 과정은 우선 현재 스택에서 팝한 이제까지의 경로에 담긴 좌표들과의 계산 비교를 통해서 조건을 충족시키는 다음 행의 좌표들을 선별하는 것이 필요하다. 조건을 충족해서 선별된 좌표 리스트는 경로에 덧잇고 다시 스택에 넣는다.
- 열이 겹치지 않는다.
- 대각선이 겹치지 않는다.
또한, 백트랙킹 조건이 필요하다. 백트랙킹이 while문 안에서 가지는 의미는, 반복의 분기를 if문 혹은 continue 등으로 다음 반복 분기로 넘어가는 것을 뜻한다. 즉, 다음 행에 퀸을 배치할 수 있는 어떤 좌표도 존재하지 않으면 백트랙킹을 수행해야 한다.
이상의 조건들을 정리한 의사코드는 아래와 같게 될 것이다.
stack = [] # DFS용 스택
path = [] # 좌표 리스트 담기 위한 경로 리스트
result = [] # 모든 경로를 담기 위한 정답 리스트
for i in range(n):
stack.append([[0, i]])
while: stack
현재 경로 좌표 팝
# 퀸을 n개 배치하였는가
if 경로 길이가 n인가:
result.append(경로)
continue
다음 행 단계의 좌표들 리스트 추출
다음 단계 좌표들 중 조건 만족하는 리스트 선별
# 조건을 만족하는 다음 단계 좌표가 있는가
if 리스트 길이가 0인가:
# 팝한 상태로 두면 저 경로는 볼 일이 없어짐
continue
for 다음 행 단계 조건 충족 좌표들:
현재 경로.append(다음 행 단계 좌표)
stack.append(업데이트된 경로)(6) 일부 수정 및 문제풀이 적용
실제 상기의 의사코드를 바탕으로 코드를 짜니, 정답은 나오지만 시간복잡도에서 발목을 붙잡혔다. 어떤 부분이 문제인지 고민을 해보고 비교를 해보니, 체스보드의 묘사를 위한 이중 리스트 자체가 시간적, 메모리적으로 소모가 크다는 것을 짐작할 수 있었다. 중첩 인덱스로 검색을 하는 건 결국 중첩 반복문과 유사하므로 O(N^2)의 시간복잡도가 걸릴 것이라 생각하고, 좀 더 간단하게 나타낼 방법을 구상했다.
그래서 아예 리스트를 단일 리스트로 두고, 인덱스를 행의 정보, 해당 요소의 값을 열의 정보로도 충분히 표현이 가능할 것이라고 판단하고 수정 작업에 들어갔다.
풀이 링크는 아래 참조!
