
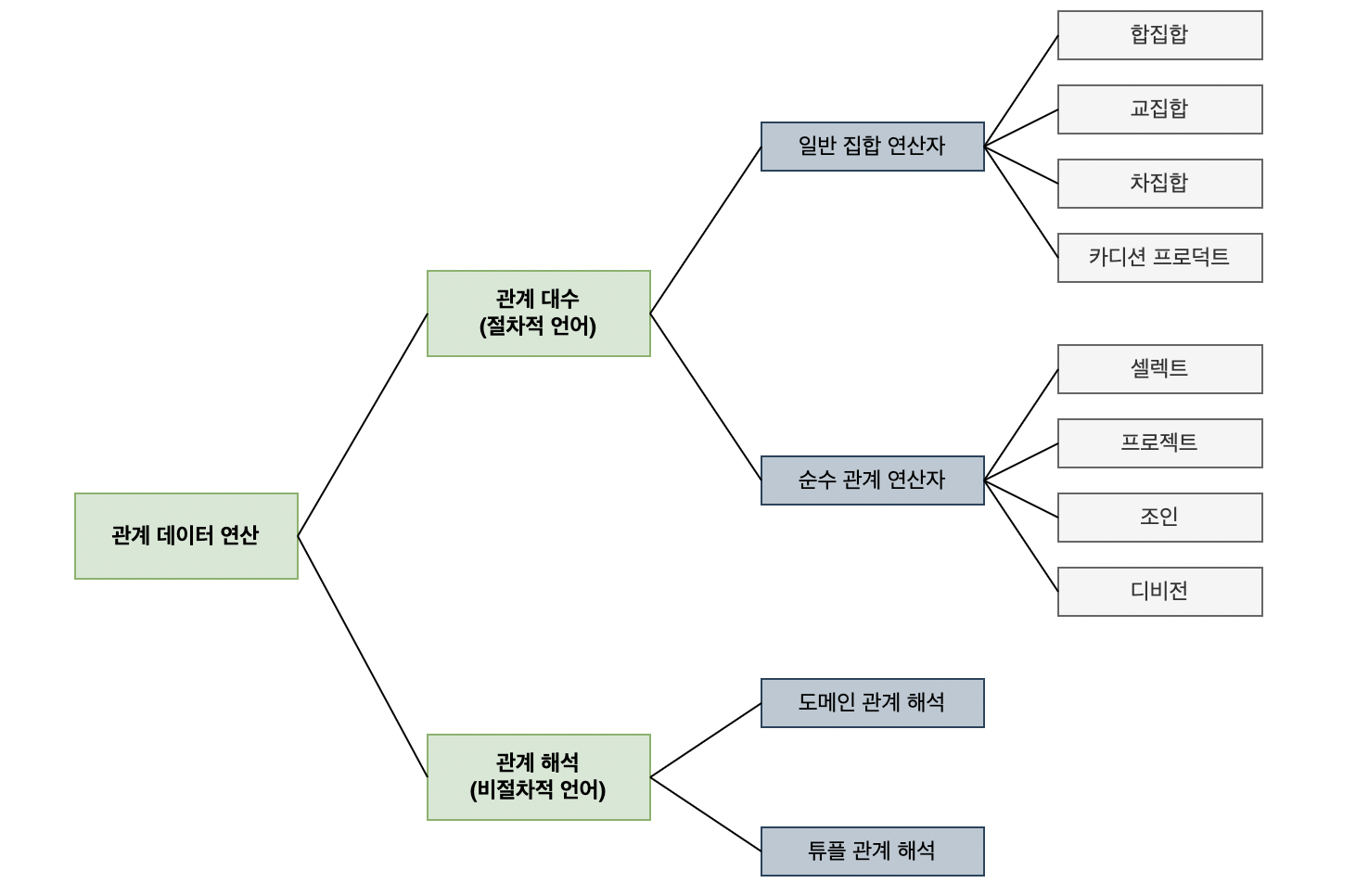
DML을 설명할 때, 절차적 언와와 비절차적 언어로 나누어 지는 것을 설명한 적 있습니다. 절차적 언어는 사용자가 원하는 데이터를 얻기 위해 어떻게 처리해야 하는지에 명세를 하고, 비절차적 언어는 결과에만 집중을 하는 언어입니다. 위의 그림에서 알 수 있듯이 관계 대수가 절차적 언어이며 관계 해석이 비절차적 언어의 역할을 하게 됩니다.
1. 관계 데이터 연산의 개념
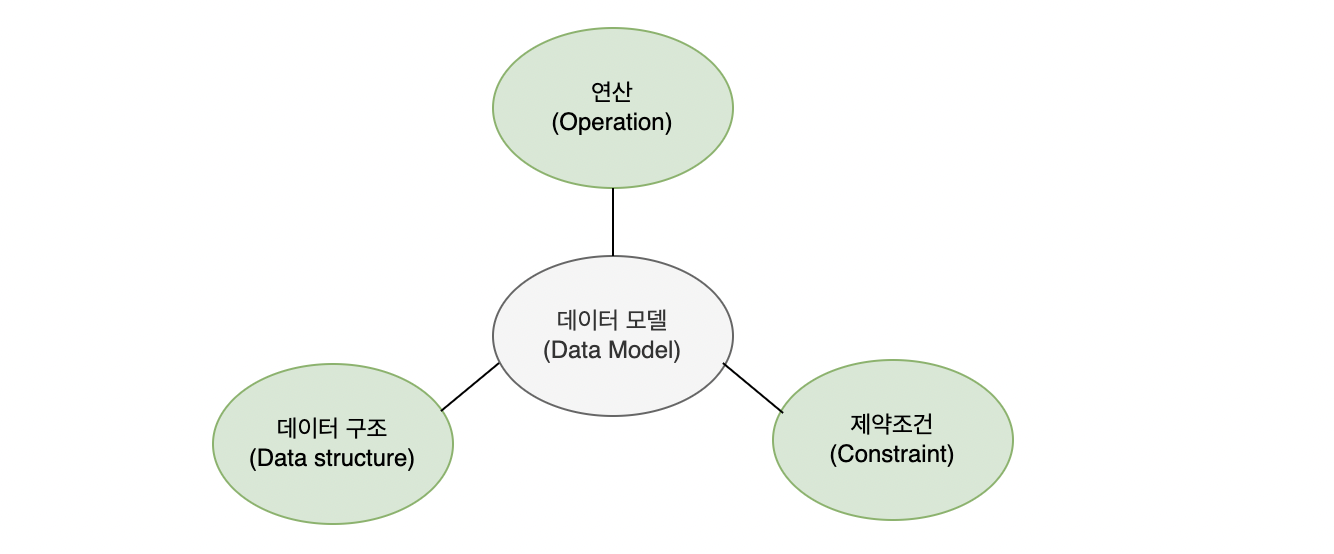
지난 강의에서 데이터 구조(릴레이션의 구조, 정규화), 제약조건(개체/참조 무결성 제약)에 대해서 살펴 보았습니다. 이번 시간에는 연산에 대해서 학습해보겠습니다.
1.1. 관계 데이터 연산
관계 데이터 연산은 원하는 데이터를 얻기 위해 릴레이션에 필요한 처리 요구를 수행하는 것을 말합니다. 이러한 관계 데이터 연산은 크게 관계 대수와 관계 해석이 있습니다.
관계 대수는 원하는 결과를 얻기 위해 데이터 처리 과정을 순서대로 기술하는 것을 의미하며, 관계 해석은 원하는 결과를 얻기 위해 처리를 원하는 데이터가 무엇인지만 기술하는 것을 의미합니다. 즉, 처리절차를 얼마나 자세히 기술하느냐에 따라 구분되어 집니다.
2. 관계 대수 (relational algebra)
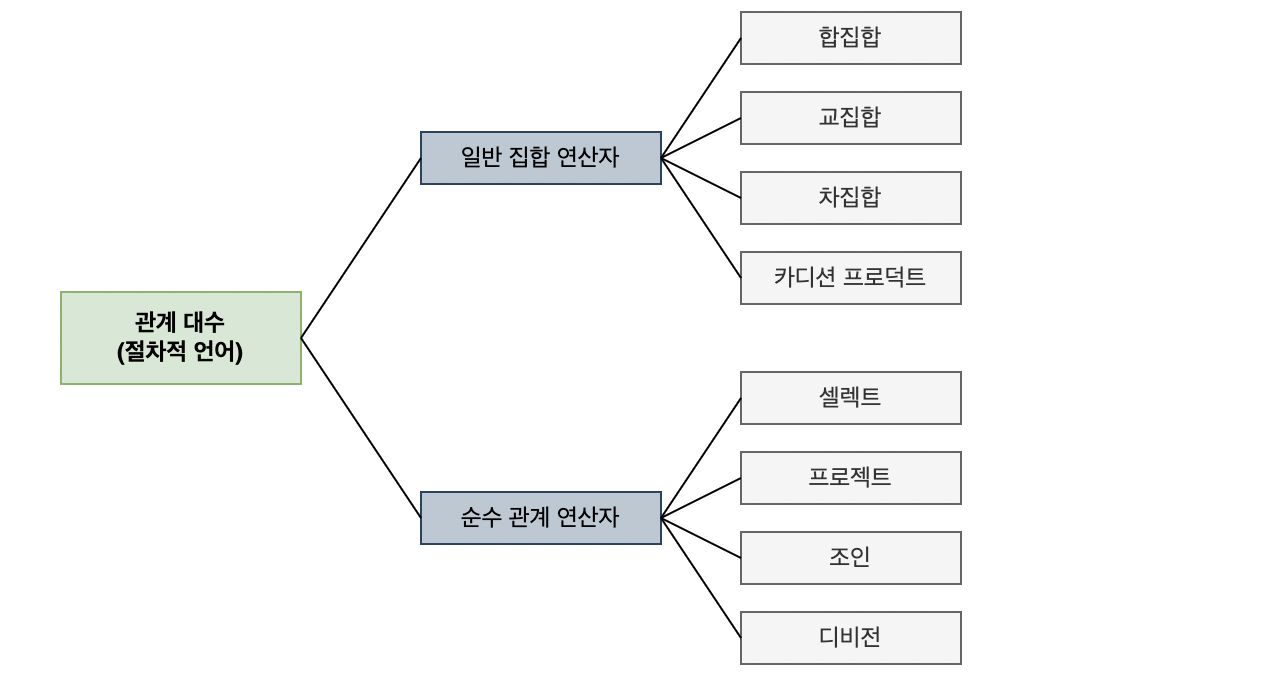
관계 대수는 절차 언어 (procedural language)입니다. 릴레이션을 절차적으로 처리하기 위해 사용하는 연산자는 대표적으로 8개가 존재하고 이들은 일반 집합 연산자와 순수 관계 연산자로 분류됩니다.
관계 대수는 폐쇄 특성(closure property)가 존재합니다. 폐쇄 특성이란 피연산자도 릴레이션이고 연산의 결과도 릴레이션인 특징을 말합니다.
2.1. 일반 집합 연산자 (set operation)
일반 집합 연산자는 릴레이션이 튜플의 집합이라는 개념을 이용하는 연산자입니다.
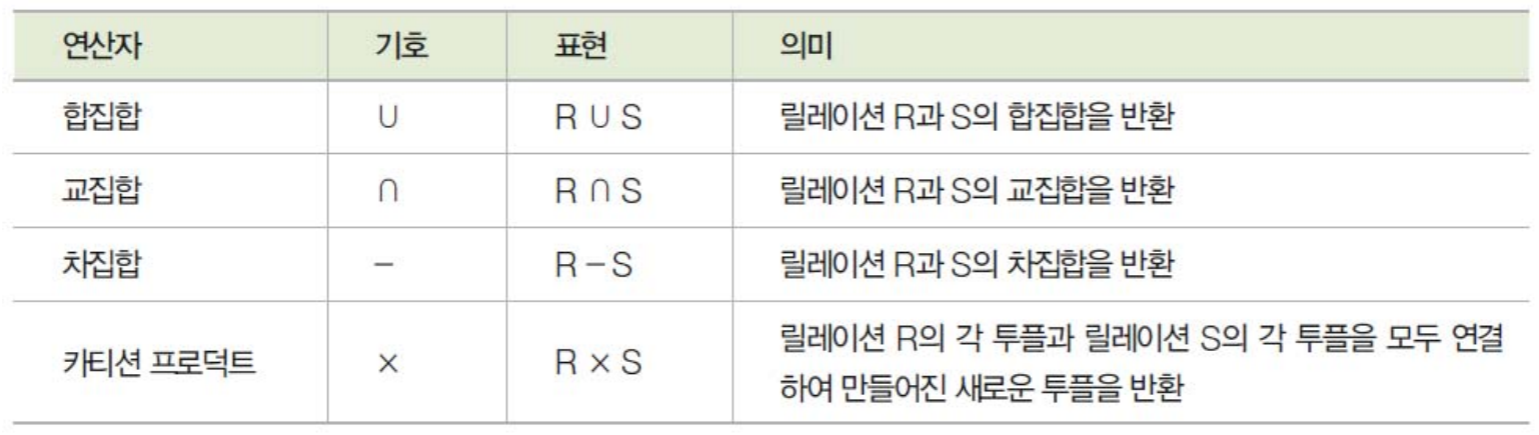
일반 집합 연산자의 특성
-
피연산자(릴레이션)가 두 개 필요하다.
-
합집합, 교집합, 차집합은 피연산자인 두 릴레이션이 합병이 가능해야 한다.
- 합병 가능 조건 : 차수, 도메인이 같아야 한다.
결과 릴레이션의 특성
합집합 (Union)
-
결과 릴레이션의 차수는 R과 S의 차수와 같다.
-
카디널리티는 R과 S의 카디널리티를 더한 값 보다 같거나 작다.
-
합집합 연산은 교환/결합 법칙이 가능하다.
교집합 (intersection)
-
결과 릴레이션의 차수는 R과 S의 차수와 같다.
-
카니덜리티는 R과 S의 어떤 카디널리티보다 크지 않다.
-
교집합 연산은 교환/결합 법칙이 가능하다.
차집합 (difference)
-
결과 릴레이션의 차수는 R과 S의 차수와 같다.
-
R-S의 카디널리티는 릴레이션 R의 카디널리티와 같거나 작다.
-
S-R의 카디널리티는 릴레이션 S의 카디널리티와 같거나 작다.
-
차집합 연산은 교환/결합 법칙이 성립하지 않는다.
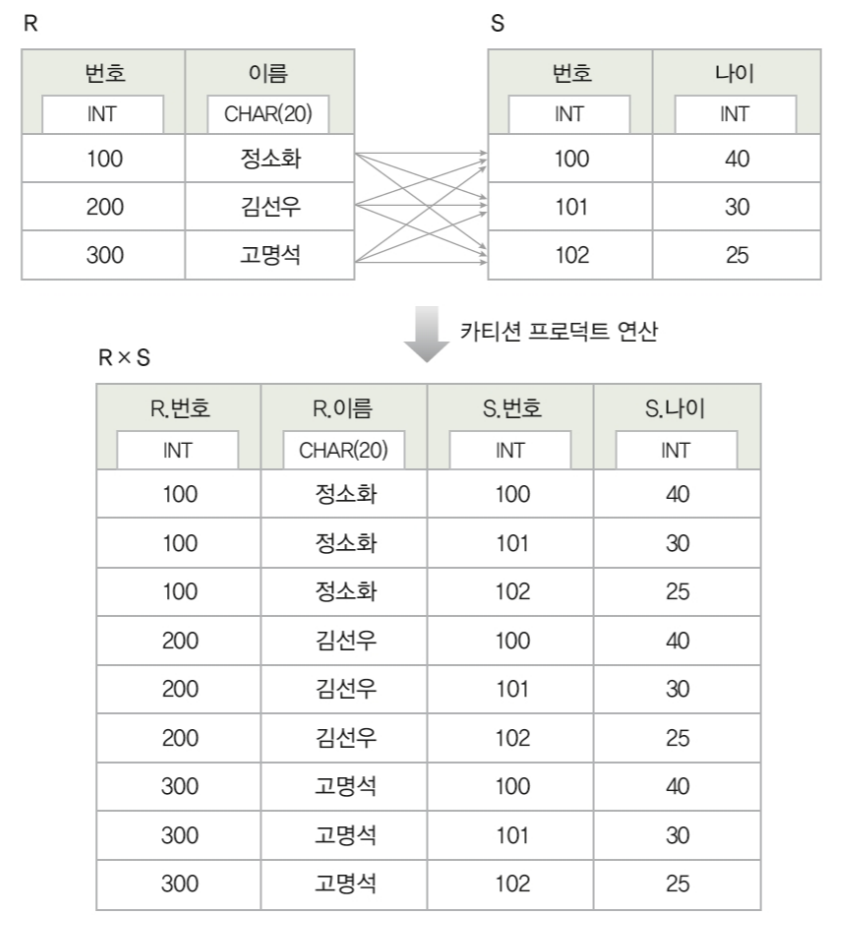
카티션 프로덕트(cartesian product)
-
결과 릴레이션의 차수는 R과 S의 차수를 더한 것과 같다.
-
카디널리티는 릴레이션 R과 S의 카디널리티를 곱한 것과 같다.
-
카티션 프로덕트 연산은 교환/결합 법칙이 성립한다.
2.2. 순수 관계 연산자 (relational operation)
순수 관계 연산자는 릴레이션의 구조와 특성을 이용하는 연산자입니다.
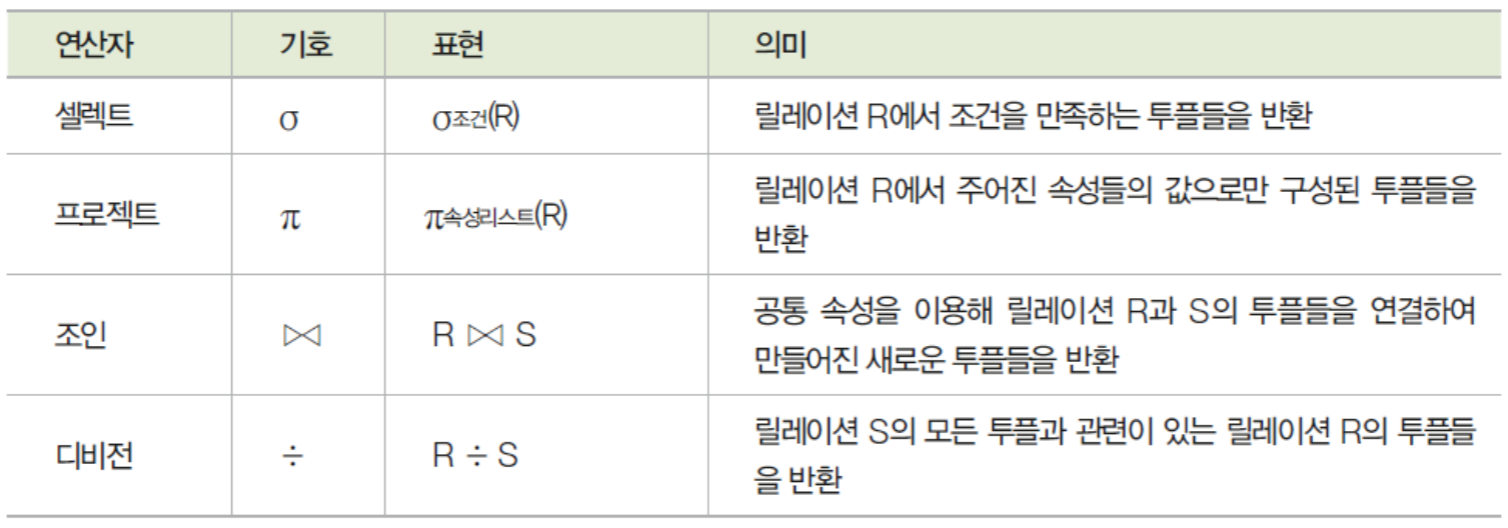
순수 관계 연산자 특성
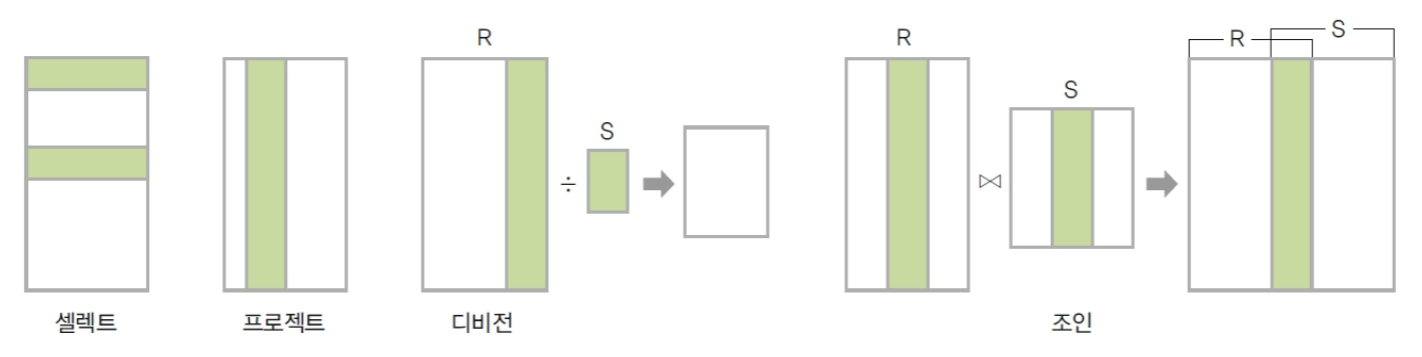
셀렉트
-
릴레이션에서 조건을 만족하는 튜플만 선택하여 결과 릴레이션을 구성
-
하나의 릴레이션을 대상으로 연상을 수행
-
수평적 연산
-
셀렉트 조건을 프레디키트(predicate)라고도 함
-
데이터 언어적 표현법 : where 조건식
-
조건식 : 비교/논리 연산자 사용
-
예시 : 고객 릴레이션에서 등급이 gold인 사람만 반환
where 등급='gold'
프로젝트
-
릴레이션에서 선택한 속성의 값으로 결과 릴레이션을 구성
-
하나의 릴레이션을 대상으로 연산을 수행
-
수직적 연산
-
데이터 언어적 표현법 : 릴레이션[속성리스트]
-
예시 : 고객 릴레이션에 고객이름, 등급, 적립금만 반환
고객[고객이름,등급,적립금]
조인
-
조인 속성을 이용해 두 릴레이션을 조합하여 결과 릴레이션을 구성
-
조인 속성을 두 릴레이션이 공통으로 가지고 있는 속성을 의미
-
자연 조인이라고도 함
-
외래키와 기본키의 연결로 조인을 할 수 있음
-
예시 : 주문 릴레이션의 주문 고객(외래키)과 고객 릴레이션의 고객아이디(기본키)를 연결하여 결과 릴레이션 구성
디비전
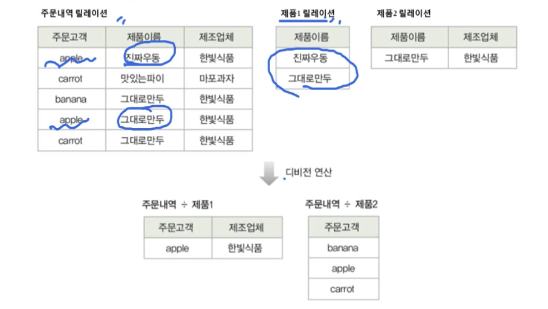
-
릴레이션 1 % 릴레이션 2로 표현할 수 있음 -
릴레이션2의 모든 튜플과 관련이 있는 릴레이션1의 튜플로 결과 릴레이션을 구성
-
릴레이션1이 릴레이션2의 모든 속성을 포함하고 있어야 연산이 가능함
2.3. 조인(join)의 종류
-
세타(theta) 조인 : 6가지 비교 연산자를 이용하여 조인을 수행
-
동등(equi) 조인 : 그 중 속성이 같은(=) 경우
-
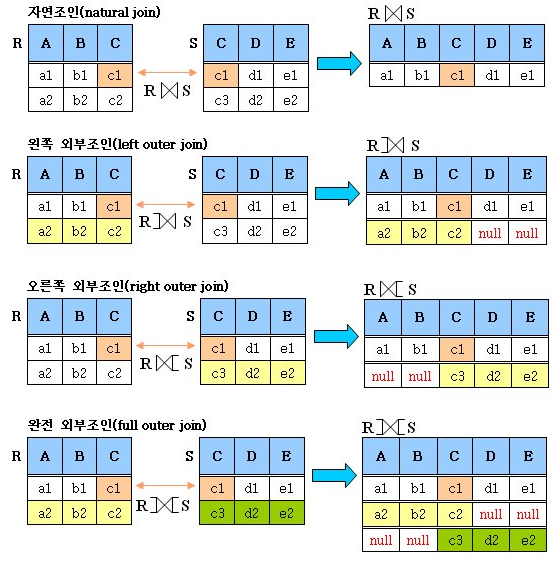
자연(natural) 조인 : 같은 경우로 묶다 보면 같은 속성이 2개 생겨서 하나를 제외하는 조인
-
-
외부(outer) 조인
-
왼쪽 외부(left outer) 조인 : 왼쪽 튜플 기준으로 자연 조인하고 불가능한 값은 null 처리하여 반환
-
오른쪽 외부(right outer) 조인 : 오른쪽 튜플 기준으로 자연 조인하고 불가능한 값은 null 처리하여 반환
-
완전 외부(full outer) 조인 : 양쪽 튜플 기준으로 자연 조인하고 불가능한 값은 null 처리하여 반환
-
-
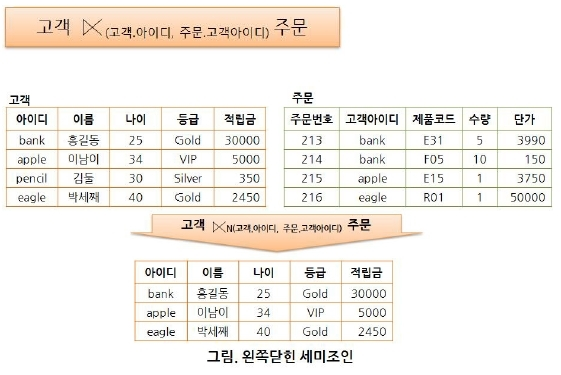
세미(semi) 조인 : 자연조인을 한 후 두 릴레이션 중 한쪽 릴레이션 결과만 반환
2.4. 관계 대수의 한계
-
관계 대수는 산술 연산을 할 수 없음
-
집단 함수(aggregate function)를 지원하지 않음
-
정렬을 나타낼 수 없음
-
프로젝트 연산의 결과에 중복된 튜플을 나타내지 못함
위와 같은 한계점으로 조금 더 확장된 관계 대수는 집단 함수(AVG, MAX ...)와 그룹화(grouping)을 추가하여 사용될 수 있다.
3. 관계 해석
관계 해석은 원하는 데이터가 무엇인지만 선언하는 언어입니다. 일반적으로 관계 해석에는 튜플 관계 해석, 도메인 관계 해석이 있습니다.
일반적으로 관계 해석은 비절차적 언어이기 때문에 컴퓨터가 그대로 이해하고 실행할 수 없어 절차적 언어나 SQL문으로 변환하여야 합니다. 대부분 관계 대수를 사용하고 있기 때문에 관계 해석에 대해서는 아래의 그림으로만 설명하겠습니다.
