이 문제는 풀다가 너무 이해가 안가서.. 한번 풀고는 구글링을 한 후 두세번 다시 풀고 나서야 이해가 되었던 문제이다.
문제 설명
섬으로 이루어진 나라가 있고, 모든 섬을 다리로 연결하려고 한다. 이 나라의 지도는 N×M 크기의 이차원 격자로 나타낼 수 있고, 격자의 각 칸은 땅이거나 바다이다.
섬은 연결된 땅이 상하좌우로 붙어있는 덩어리를 말하고, 아래 그림은 네 개의 섬으로 이루어진 나라이다. 색칠되어있는 칸은 땅이다.
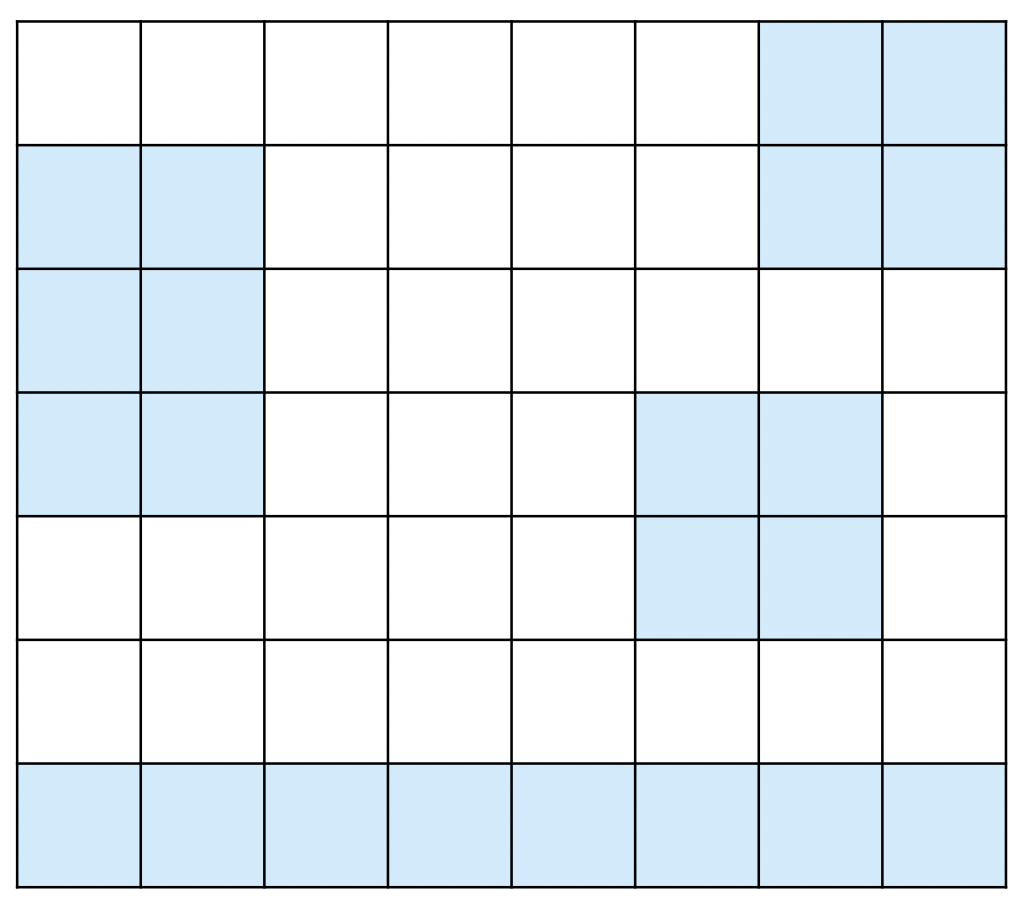
다리는 바다에만 건설할 수 있고, 다리의 길이는 다리가 격자에서 차지하는 칸의 수이다. 다리를 연결해서 모든 섬을 연결하려고 한다. 섬 A에서 다리를 통해 섬 B로 갈 수 있을 때, 섬 A와 B를 연결되었다고 한다. 다리의 양 끝은 섬과 인접한 바다 위에 있어야 하고, 한 다리의 방향이 중간에 바뀌면 안된다. 또, 다리의 길이는 2 이상이어야 한다.
다리의 방향이 중간에 바뀌면 안되기 때문에, 다리의 방향은 가로 또는 세로가 될 수 밖에 없다. 방향이 가로인 다리는 다리의 양 끝이 가로 방향으로 섬과 인접해야 하고, 방향이 세로인 다리는 다리의 양 끝이 세로 방향으로 섬과 인접해야 한다.
섬 A와 B를 연결하는 다리가 중간에 섬 C와 인접한 바다를 지나가는 경우에 섬 C는 A, B와 연결되어있는 것이 아니다.
아래 그림은 섬을 모두 연결하는 올바른 2가지 방법이고, 다리는 회색으로 색칠되어 있다. 섬은 정수, 다리는 알파벳 대문자로 구분했다.
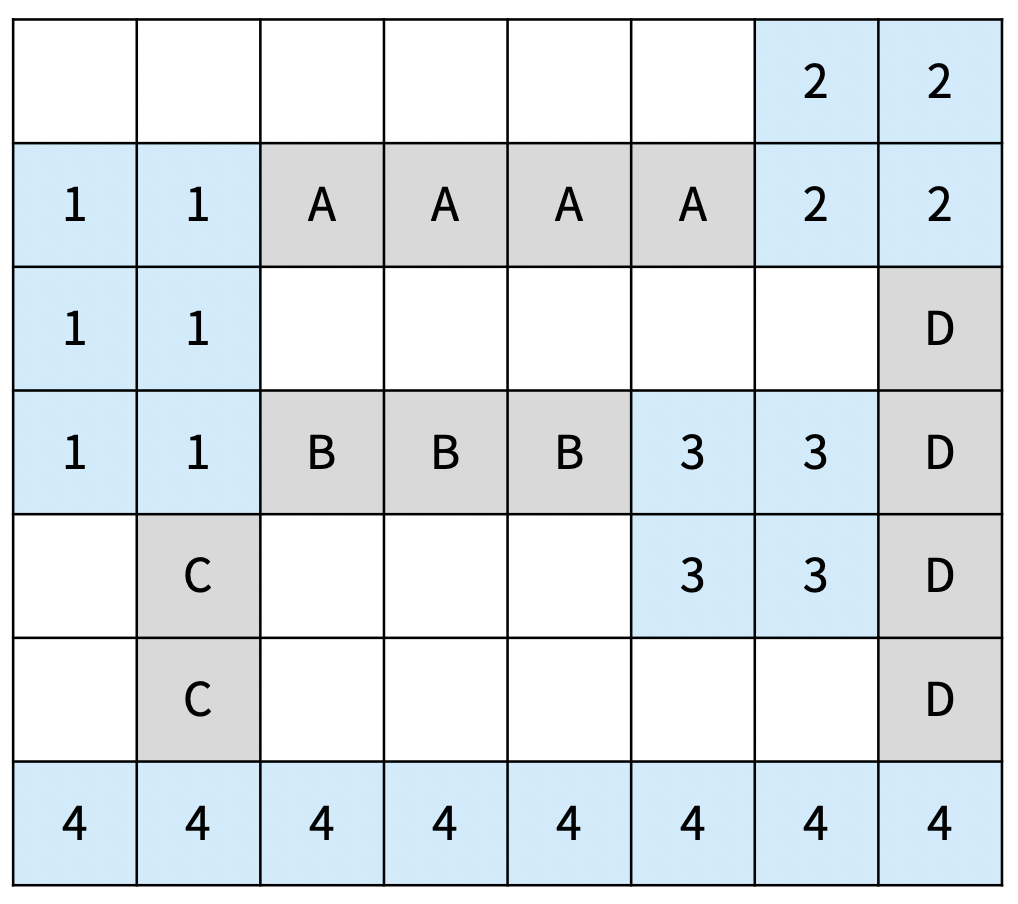
다리의 총 길이: 13
D는 2와 4를 연결하는 다리이고, 3과는 연결되어 있지 않다.
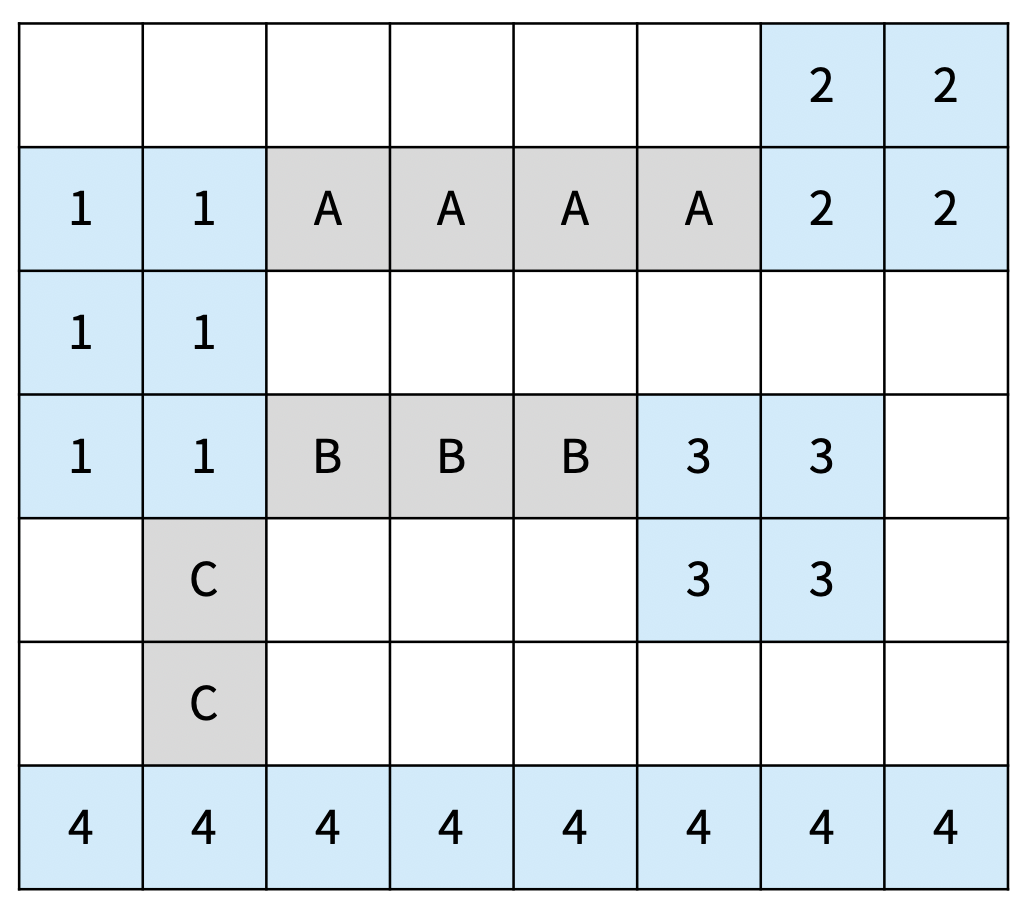
다리의 총 길이: 9 (최소)
나라의 정보가 주어졌을 때, 모든 섬을 연결하는 다리 길이의 최솟값을 구해보자.
입력
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
출력
모든 섬을 연결하는 다리 길이의 최솟값을 출력한다. 모든 섬을 연결하는 것이 불가능하면 -1을 출력한다.
제한
1 ≤ N, M ≤ 10
3 ≤ N×M ≤ 100
2 ≤ 섬의 개수 ≤ 6
예제 입력 1
7 8 0 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
예제 출력 1
9
문제 풀이
해당 문제는 총 3부분으로 나누어서 풀었어야 했다.
각 섬들을 나누어서 indexing하는 부분 (ex) 1번섬, 2번섬 , 3번섬 이런 식으로..)
해당 섬들의 index가 결국 그래프의 노드가 된다.-
각 섬들을 연결할 다리의 길이를 찾는 부분
다리의 길이는 가중치가 된다.
-
1-2에서 찾은 부분들을 연결해서 최소 신장트리 알고리즘 (크루스칼 혹은 프림) 을 적용해서 각 섬들을 한번에 연결할 수 있는 최소의 다리의 길이를 구하는 부분
이렇게 분리를 해서 보니 쉬웠지만.. 해당 문제를 직접 풀때는 너무 어려웠다.
처음 나의 풀이는 제대로 문제를 보지 않고 풀어서.. maxX , maxY , minX, minY를 뽑아서 무조건 사각형이 만들어진다고 생각하고 풀어서.. 섬들이 사각형을 이루는 예제 1, 2, 4는 풀어졌으나 3이 풀리지 않았다.
어떻게 섬과 섬사이를 연결하는 다리의 길이를 결정해야 할 지 헤매다가 결국 구글링을 하였고 그 해답은 바로
섬의 모든 정점들에서 네 방향으로 뻗어나가면서 다른 섬을 만났을 때 그 거리를 구하는 것이였다.. 결국 브루트포스한 방법으로 해결했는데.. 이것 말고도 더 효율적인 방법이 있을 것 같다.. 최적화가 필요해 보이긴한다.
하기는 작성한 코드이다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class exam02 {
//각 섬들의 연결된 섬과 다리길이를 저장하는 노드 클래스
static class Node{
int idx;
int len;
public Node(int idx, int len) {
this.idx = idx;
this.len = len;
}
// 이 부분은 출력을 위하여 작성하였다.
@Override
public String toString() {
return "Node{" +
"idx=" + idx +
", len=" + len +
'}';
}
}
//모든 방향을 보아야하기에 dirs로 상 , 하 , 좌 , 우를 미리 선언하였다.
final static int[][] dirs = {{1,0},{0,1},{-1,0},{0,-1}};
static int[][] board;
static List<List<Node>> graph;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
board = new int[N][M];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < M; j++) {
board[i][j] = Integer.parseInt(st.nextToken());
}
}
// 각 섬들을 찾고 구분 짓는 부분
int idx = 2; //처음에 섬의 번호를 2번부터 시작하고 추후 graph에 넣어줄때는 1씩 빼줄 것이다.
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if(board[i][j] == 1){
board[i][j] = idx;
dfs(i,j,idx++); // 각 섬을 구분지을 dfs
}
}
}
graph = new ArrayList<>();
for (int i = 0; i < idx; i++) {
graph.add(new ArrayList<>());
}
//각 섬들을 연결할 다리의 길이를 찾는 로직
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if(board[i][j] != 0){
connectBridge(i,j,board[i][j]);
}
}
}
//answer 값이 0이면 모든 섬들이 연결되지 않았다는 의미이다.
int answer = prim(1,idx-1);
System.out.println(answer == 0? -1 : answer);
}
public static int prim(int start , int v){
int weightSum = 0;
int cnt = 0; // 모든 섬들이 연결되었는지 확인할 cnt 변수
PriorityQueue<Node> pq = new PriorityQueue<>((x,y) -> x.len - y.len);
boolean[] visited = new boolean[graph.size()];
pq.add(new Node(start,0));
while (!pq.isEmpty()){
Node cur = pq.poll();
if(visited[cur.idx]){
continue;
}
cnt++;
visited[cur.idx] = true;
weightSum += cur.len;
for (int i = 0; i < graph.get(cur.idx).size(); i++) {
Node adj = graph.get(cur.idx).get(i);
if(!visited[adj.idx]){
pq.add(adj);
}
}
}
//모든 섬들이 연결되었다면 cnt는 모든 섬의 갯수 - 1 이 되어야한다.
return cnt == v-1 ? weightSum : 0;
}
public static void connectBridge(int x, int y, int idx){
Queue<int[]> queue = new LinkedList<>();
for(int[] dir : dirs){
queue.offer(new int[]{x,y,0});
// 이 부분이 포인트이고 내가 몰랐던 부분인데..
// 이렇게 해주면 한 방향으로 쭈욱 간다.
while (!queue.isEmpty()){
int[] cur = queue.poll();
int xNext = cur[0] + dir[0];
int yNext = cur[1] + dir[1];
int moveCnt = cur[2];
if(xNext < 0 || yNext < 0 || xNext >= board.length || yNext >= board[x].length){
continue;
}
if(board[xNext][yNext] != idx){
if(board[xNext][yNext] != 0){
int from = idx-1; //아까 말했듯 각 섬들의 번호 -1 (2부터시작해서..)
int to = board[xNext][yNext]-1;
int len = moveCnt;
if(moveCnt >= 2){
//moveCnt가 2이상이여야 하므로
graph.get(from).add(new Node(to,len));
}
}else {
queue.add(new int[]{xNext,yNext,moveCnt+1});
}
}
}
}
}
public static void dfs(int x, int y, int idx){
for(int[] dir : dirs){
int xNext = x + dir[0];
int yNext = y + dir[1];
if(xNext < 0 || yNext < 0 || xNext >= board.length || yNext >= board[x].length){
continue;
}
//값이 1이면 지정해놓은 섬 번호로 바꿔주고 다시 dfs를 돌리면 주변의 값이 1인 값들은
//모두 idx로 값이 변하게 된다.
if(board[xNext][yNext] == 1){
board[xNext][yNext] = idx;
dfs(xNext,yNext,idx);
}
}
}