학습 목표
1. Existence and Uniqueness Question을 해결하기 위한 과정을 이해하고 설명할 수 있다.
2. Row Reduction Algorithm의 각 단계를 이해하고 의미를 설명할 수 있다.
3. 방정식의 Existence 와 Uniqueness를 Determine하고 Solution set을 구할 수 있다.

---

1. 개념

Echelon Form (E.F.)의 3가지 Properties (Conditions)

1. all nonzero rows are above any rows of all zeros.
2. each leading entry of a row is a column to the right of the leading entry of the row above it.
3. all entries in a column below a leading entry are zeros.

✅ E.F. 단계에서 linear system의 existence를 판단할 수 있다.

Reduced Echelon Form (R.E.F.)의 3가지 Properties (Conditions)

1. the leading entry in each nonzero is 1.
2. each leading 1 is the only nonzero entry in its column.

✅ R.E.F 단계에서 linear system의 uniqueness를 판단할 수 있다.

2. 주의할 특성

1. Any nonzero matrix may be row reduced(transformed by E.R.O.) into more than one matrix in echelon form.
2. However, the reduced echelon form one obtains from a matrix is unique!

🚩 THEOREM 1 : Uniqueness of the Reduced Echelon Form.

Each matrix is row equivalent to one and only one Reduced Echelon Matrix.

While doing E.R.Os on specific order, it can result to various echelon form.
But it doesn’t matter since the reduced echelon form is unique.

3. 개념

1. pivot position : R.E.F에서 location in matrix that corresponds to leading 1. (pivot)
2. pivot column : R.E.F에서 column of matrix that contains a pivot position.

4. 방법론

Row Reduction Algorithm(R.R.A.)

Existence 와 Uniqueness를 E.F. 과 R.E.F.을 통해 판단하기 위한 알고리즘.(= 가우시안 소거법, Gaussian Elimination)

• Follows consists of four steps, and it produces a Echelon Matrix (forward phase).
• A fifth step produces a Reduced Echelon Matrix (back-ward phase).

Step of the R.R.A

1. Begin with the leftmost nonzero column. This is a pivot column. The pivot position is at the top.
2. Select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry onto the pivot position.
3. Use row replacement operations to create zeros in all positions below the pivot.
4. Cover(or ignore) the row containing the pivot position and cover all rows, if any, above it. Apply 1-3 to the sub-matrix that remains. Repeat the process until there are no more nonzero rows to modify. (E.F.)
5. Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by a scaling operation. (R.E.F.)

✅ Step 2 주의사항. Partial Pivoting
round-off error 를 줄이기 위해 a computer program usually selects a pivot the entry in a column having the largest absolute value.

4. 해의 표기법과 변수

Solutions of Linear Systems

• basic variable : matrix에서 pivot columns과 일치(상응)된다.
• free variable : free to choose any value. variables에 대해 제약을 없앤다.

✅ free variable의 존재 유무로 uniqueness를 determine할 수 있다.

Parametric Descriptions of Solution Sets

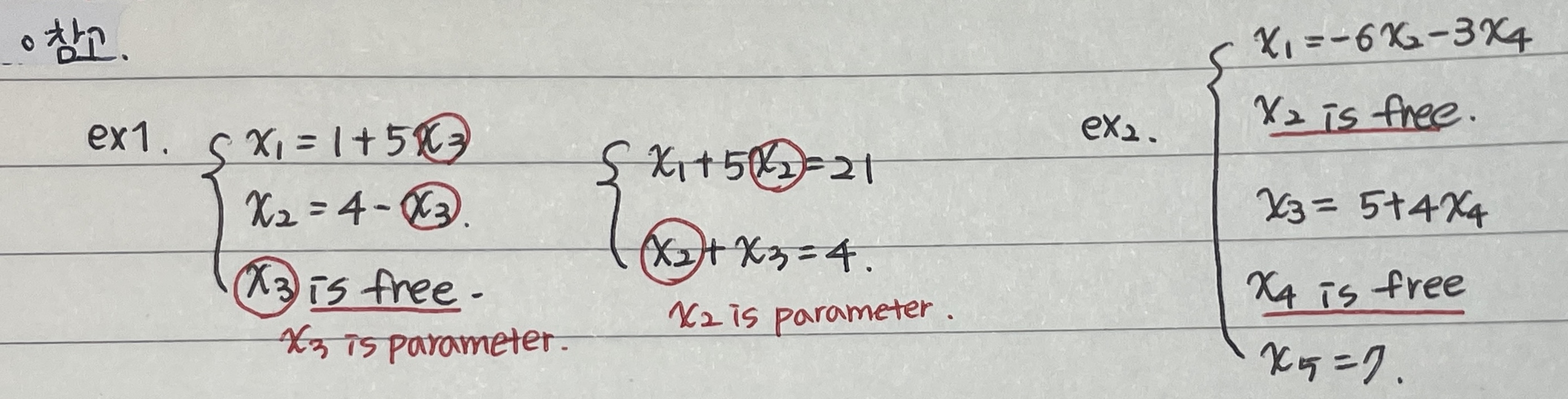
• ex1., ex2.는 free variable이 parameter 역할을 하는 solution sets에 대한 Parametric Descriptions이다.
  → solve for variables in terms of parameter.

✅ System이 consistent(=solution set이 !empty) & free variables를 가질 경우, solution은 많은 parametric descriptions를 가진다.
⇒ Not a single/unique parametric description.

🚩 THEOREM 2 : Existence and Uniqueness Theorem.

Existence (E.F.)

A linear system is consistent. ↔
The rightmost column of the augmented matrix is not a pivot column. ↔
An echelon form of the augmented matrix has no row of the form [0 … 0 b] with b nonzero.

Uniqueness (R.E.F.)

If consistent,

1. Free variables : infinitely many solutions.
2. N-free variables : solution set contains unique(exactly one) solution.

---