1. Ridge Regression

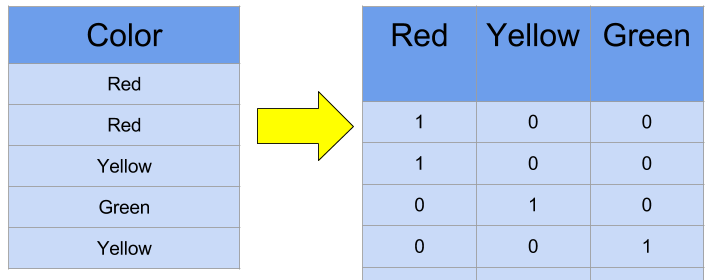
1.1 One-hot encoding

• 범주형 데이터를 분석할 수 있도록 인코딩해준다.(이진화)
• 컴퓨터가 이해할 수 있도록, 'Busan', 'Seoul', 'Daegu' 등을 0과 1로 표현함.
• pandas get_dummies/category_encoders/sklearn(scikit-learn) 등을 사용한다.
• 유의사항: 집합의 크기(Cardinality)가 작을 때 사용한다. 서울, 대전, 대구 3개는 컬럼이 3개까지 생겨서 괜찮지만, 전 세계 200개 국가는 컬럼이 200개가 생기면 오히려 분석에 방해가 된다.(차원의 저주)
• 범주형(Categorical data) 자료
  명목형(Norminal): 성별, 도시, 혈액형 등 (숫자의 크기에 의미가 없다.)
  순서형(Ordinal): 수능 등급, 신체 등급, 한우 등급... (숫자의 크기에 의미가 있다.)

1.2 Feature selection

• 특성공학은 내가 해결하고 싶은 문제에 적합한 특성(컬럼)을 만들어 내는 것을 의미한다. 실제 업무에서 가장 많은 시간을 할애하는 작업이기도 하다.
• SelectKBest 사용
  K개의 중요한 특성을 고른다. 단순히 타겟 변수와의 상관관계로 정하지는 않고 각종 통계치(F-statistics, P-value 등을 사용한다.)
  좋은 특성이란?: 독립 변수들끼리의 상관성이 낮고(다중공선성 문제), 타겟과의 상관성은 높은 특성(Feature)
• 다중공선성(Multicollinearity)
  회귀분석에서 독립변수들 사이에 강한 상관관계가 나타나는 것을 의미한다. 왜 문제가 되냐면 회귀분석의 전제 조건(가정)을 위반하기 때문.

1.3 Ridge Regression

• https://youtu.be/Q81RR3yKn30?t=222

• Train data에 꽉 맞지 않은 새로운 Line을 찾는다.(연속형, 이산형 데이터 모두 사용 가능하다)

• 왜?: 모델이 Train data에 덜 적합되어, 과적합(Overfitting) 문제를 해소할 수 있기 때문.

• 즉, 편향을 높이고, 분산을 줄이는 방식으로 정규화(Regularization)를 수행한다.

• OLS와의 차이점:
  1. OLS는 단순히 RSS의 최소화를 추구하지만 Ridge는 RSS와 lamda*slope-squared의 최소화를 추구한다.
  2. sample의 개수가 부족할 때 OLS말고 Ridge를 사용하면 덜 민감하게 학습을 한다.

• lamda(혹은 alpha, regularization paremeter, penalty term): 패널티의 정도를 결정한다. slope^2는 기존의 최소제곱법에 페널티를 추가한다.(절편값을 빼고 모든 변수를 포함)
  0이상의 값을 가진다. 커질수록 직선의 기울기가 0에 가까워지면서 수평에 가까운(평균 기준모델) 그래프를 그리게 된다. 반면, 작아질수록 패널티가 줄어드니까, 기존 OLS와 같은 형태로 나타나게 된다.
  lamda를 정하기 위해 Cross-Validation(CV, 교차검증)을 사용한다.

• 패널티의 효과: 기울기가 가파르면 x(독립 변수)의 변화에 따른 y(타겟)의 값이 민감하게 변화한다. 패널티가 있기 때문에 기울기가 완만해지고, x에 따른 y의 변화가 기존 회귀선(OLS)보다 덜 민감해진다.

• 릿지(L2)와 라쏘(L1)의 차이 + 엘라스틱 넷

  • Ridge(릿지): 사용할 피쳐를 연구자가 직접 판단. 연구자가 확인 후 무쓸모라 판단되는 특성을 삭제해준다.
  • Lasso(라쏘): 계수의 절댓값을 규제의 기준으로 사용한다. 자동으로 특성을 선별한 후에 프로그램이 피쳐를 무쓸모라 판단하고 삭제한다. 알아서 삭제해준다는 장점이 있지만, 갑자기 사라져서 당혹스러울 수 있다. 그럴 때에는 회귀 분석을 하기전 데이터와 비교를 해서 사라진 피쳐들을 찾아주어야 함....
  • Elastic-net(엘라스틱 넷): 릿지와 라쏘를 짬뽕시킴. 규제항은 릿지와 라쏘의 규제항 두 개를 사용한다. 어느 정도로 더하느냐는 혼합비율 r을 사용해서 조율할 수 있다. r=0에 가까워지면 릿지, r=1에 가까워지면 라쏘와 같아진다.