이진 분류
- 데이터가 주어졌을 때, 해당 데이터를 두 가지 정답 중 하나로 분류하는 분류
- 예를 들어, 불량(1) 또는 정상(0) - 해당 데이터에 대한 정답이 1 과 0 중 하나라면, 해당 데이터가 1 일 확률이 출력되고, 해당 확률이 0.5 이상이면, 1로 판단
- 이러한 이진 분류에는, Binary Cross Entropy Loss(이진 교차 엔트로피 손실) 함수를 사용

다중 분류
- 데이터가 주어졌을 때, 데이터의 정답이 3가지 이상인 경우
- 색깔 데이터에 대한 정답이 빨(0) , 초(1) , 파(2) 인 경우 - 다중 분류는 소프트맥스 휘귀(Softmax Regression)라고도 부르며, 소프트 맥스 함수(Softmax Function)를 이용해 각 클래스로 예측할 확률을 계산한다.
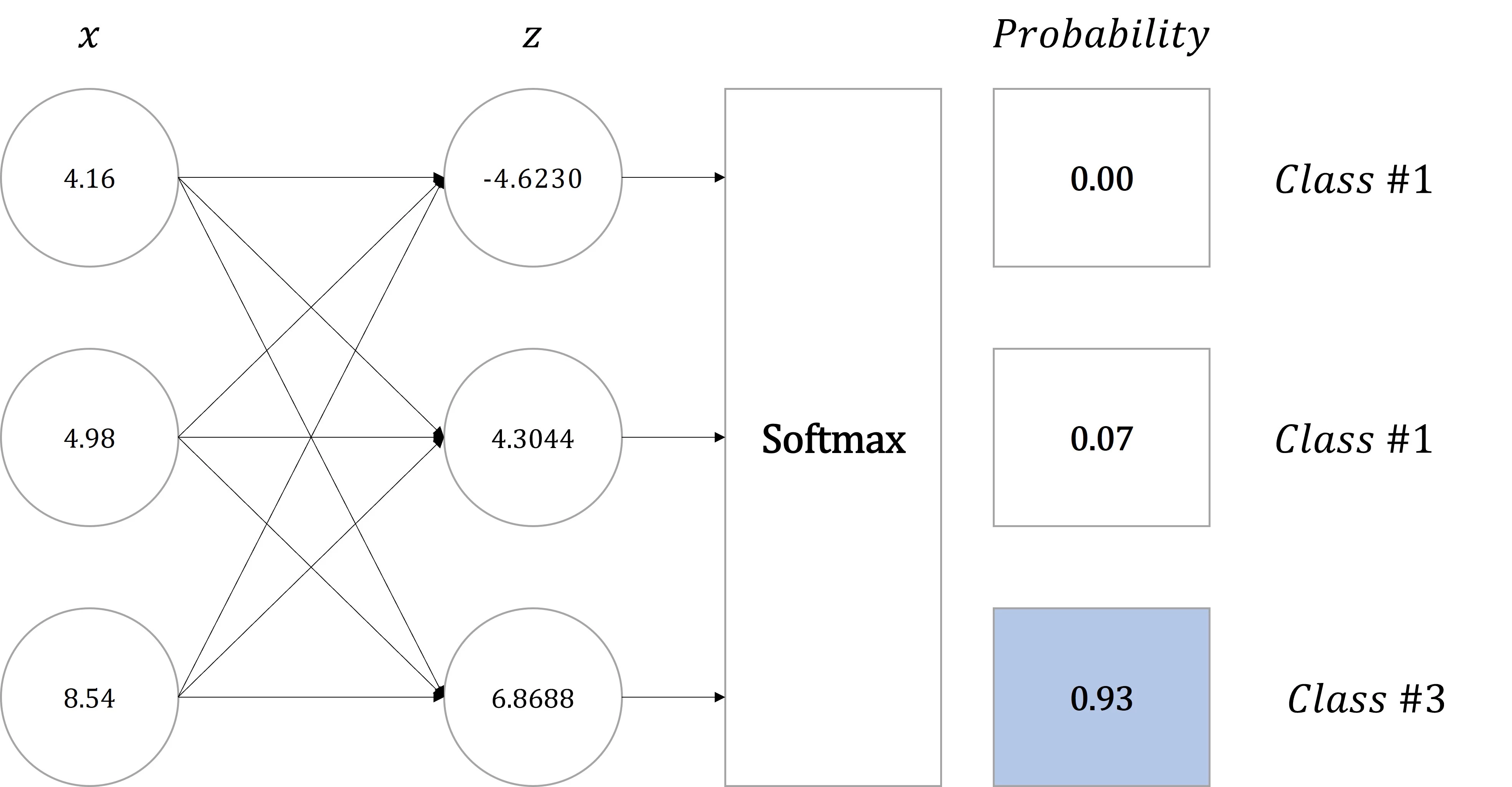
모델에서 입력값[4.16,4.98,8.54]이 이며, 출력값이[-4.623,4.3044,6.8688] 라면 세 번째(6.8688) 클래스에 포함되는 것은 알 수 있으나, 얼마나 높은 정확도로 세 번째(6.8688)에 클래스가 되는지 확인하기 어렵다.
그러므로 이 값을 확률의 형태로 변환하기 위해 소프트맥스 함수(Softmax Function)를 적용한다.
소프트맥스 함수(Softmax Function)의 수식은 다음과 같다.
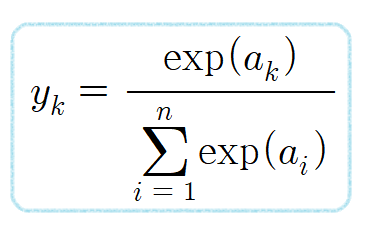
소프트 맥스 함수는 모든 값의 합을 나누게 되므로 1~n까지의 클래스 합을 모두 더하면 1이 된다.
간략하게 설명한다면 출력값 의 값의 합계가 1이 되도록 재조정하는 작업이다.
위 그림에서 적용한 벡터값을 소프트맥스 함수(Softmax Function)를 적용하면 다음과 같습니다.
p1 = (e^-4.623) / (e^-4.623 + e^4.3044 + e^6.8688) = 0
p2 = (e^4.3044) / (e^-4.623 + e^4.3044 + e^6.8688) = 0.07
p3 = (e^6.8688) / (e^-4.623 + e^4.3044 + e^6.8688) = 0.93
p1+p2+p3 = 1
교차 엔트로피(Cross Entropy)
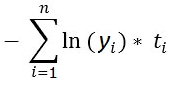
- n: 클래스 갯수
- yi : 소프트 맥스 함수에서 구한 각각의 클래스에 속할 확률
- ti : 실제값의 원-핫 벡터를 의미
- 원-핫 벡터(One-hot-Vector)란 원-한 인코딩(One-hot Encoding)을 통해 데이터가 벡터 형태로 변환된 형태
만약 세번째 클래스가 정답이라고 하면 정답 레이블이 [0,0,1]이되고
두번째 클래스가 정답이라고 하면 정답 레이블이 [0,1,0]이 된다.
그래서 세번째 클래스가 정답이라고 가정하고 오차를 계산하면
CE = -(0ln0.00 + 0ln0.07 + 1*ln(0.93)) = 0.03이 된다.
- 이 경우는 예측을 잘 했기 때문에 CE 값이 작게 나오게 된다.
2번째 클래스가 정답이라고 가정하고 오차를 계산하면
CE = -(0ln0.00 + 1ln0.07 + 0*ln(0.93)) = 1.15이 된다.
위의 경우는 입력 데이터가 1개 일 때 구한 오차 값이고 데이터의 갯수가 M개 있다고 하면 M개의 데이터에 대해서 CE(오차)값을 구한뒤 평균을 내면 전체 데이터의 CE값을 구할 수 있게 된다.
