[머신러닝 교과서] Chapter2

두두·2023년 3월 27일

본 글은 머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로을 정리한 것으로 모든 저작권은 책의 저자에게 있음을 밝힙니다.

Chap2. 간단한 분류 알고리즘 훈련

✅ 머신러닝 알고리즘을 직관적으로 이해하기
✅ 판다스, 넘파이, 맷플롯립으로 데이터를 읽고 시각화하기
✅ 파이썬으로 선형 분류 알고리즘 구현하기

수학적인 내용이 많아 이해하기 어렵다면, 다음 영상을 참고하는 것도 추천한다.
머신 러닝 교과서 3판 - 2장 간단한 분류 알고리즘 훈련 (1/2)

2.1 인공 뉴런 : 초기 머신러닝의 간단한 역사

워렌 맥컬록과 월터 피츠는 아래와 같이 처음으로 간소화된 뇌의 뉴런 개념을 발표했다.

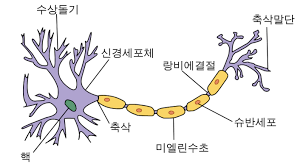
워렌 맥컬록과 월터 피츠는 신경 세포를 이진 출력을 내는 간단한 논리 회로로 표현했다.
수상 돌기에 여러 신호가 도착하면 세포체에 합쳐진다.
합쳐진 신호가 특정 임계값을 넘으면 출력 신호가 생성되고 축삭 돌기를 이용해 전달된다.

몇년 후에 프랑크 로젠블라트는 이 MCP 뉴런 모델을 기반으로 퍼셉트론 학습 개념을 발표했다.
퍼셉트론 규칙에서 로젠블라트는 자동으로 최적의 가중치를 학습하는 알고리즘을 제안했다.
이 가중치는 뉴런의 출력신호를 낼지 말지를 결정하기 위해 입력 특성에 곱하는 계수이다.

2.1.1 인공 뉴런의 수학적 정의

인공 뉴런 = 두개의 클래스가 있는 이진분류 작업

➡️ 두 클래스는 1 / -1로 나타냄
➡️ 입력 값 x와 이에 상응하는 가중치 백터 w의 선형 조합으로 결정함수를 정의
여기서 가중치가 크다 = 입력 값이 중요하다

최종 인풋(net input) z = w1x1 + w2x2 + ... + wmxm

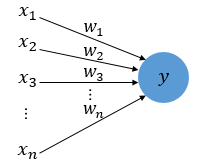
특정 샘플 x10의 최종입력이 사전에 정의된 임계 값 θ보다 크면
클래스 1로/ 그렇지 않으면 클래스 -1로 예측!

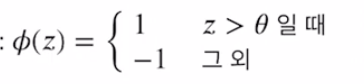
✅ 여기서 식을 간단하게 만들기 위해서 θ를 식의 왼쪽으로 옮긴다.
w0 = -θ이고 x0= 1인 0번째 가중치를 정의한다.
그러면 위에서 봤던 최종인풋 z = w1x1 + w2x2 + ... + wmxm이 다음과 같이 정리된다.

z = w0x0+ w1x1 + w2x2 + ... + wmxm
그리고 이것은 wT(w의 전치)x와 같다.
➡️ 즉, 결정 경계는 가중치인 w 값에 의해 결정된다.⭐️ (x는 미리 준비해 놓은 데이터)
이 w를 어떻게 찾을 건지를 배워야 함 (2.1.2에서 배울 것)

그러면 이제 결정함수는 다음과 같이 정리된다!

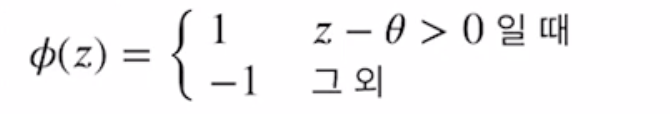
2.1.2 퍼셉트론 학습 규칙

❗️위에서도 언급했지만,
결정 경계의 값이 가중치w에 의해 결정된다.
따라서 샘플들을 잘 나누는 적절한 가중치값을 찾아야 하는데
그 방법에 대해 배워보자!

퍼셉트론 알고리즘

1️⃣ 가중치를 ( 0 ) OR ( 랜덤한 작은 값 )으로 초기화
2️⃣ 각 훈련 샘플 xi에서 다음의 작업을 함
- 출력값 ^y(y햇)을 계산
- 가중치 업데이트

j번째 가중치 wj에 대한 업데이트 값(wj의 변화량)은 다음과 같이 계산된다.

여기서,

η = 학습률 (0.0~1.0 사이 값)
yi = 진짜 클래스 레이블 (정답 값)
^yi = 예측 클래스 레이블

⭐️ 모든 가중치를 동시에 업데이트 함
= 모든 가중치가 각자 업데이트 되기 전에 예측 레이블(^y)를 다시 계산하지 않아용~

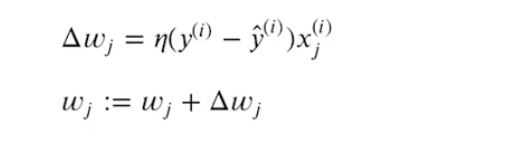
예시를 들어서 구체적으로 이해해보자

➡️ 정확하게 예측한 경우
예측 값 = 정답이 되기 때문에
가중치를 변경할 필요 ❌
즉, 다음과 같이 업데이트 값이 0이 됨

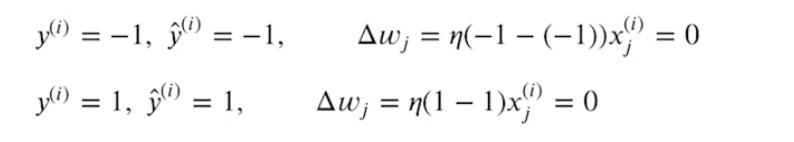
➡️ 잘못 예측한 경우
당연히 잘못 예측했기 때문에 가중치는 변경해야 함
이때 다음과 같이 양성 또는 음성 타겟 클래스 방향으로 이동시킴

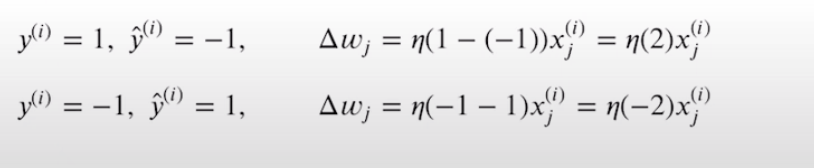
퍼셉트론은
✅ 두 클래스가 선형적으로 구분되고 학습률이 충분히 작을 때만 수렴이 보장됨.

아래 그림을 보면 잘 이해할 수 있을 것!

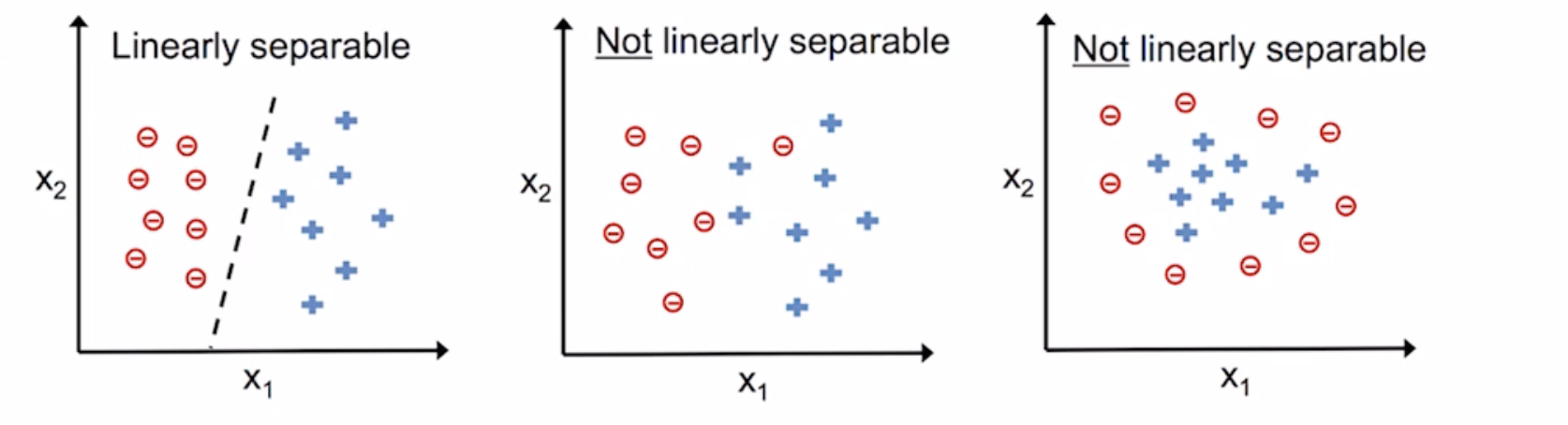
이럴 때는 훈련 데이터셋을 반복할 최대 횟수(epoch)를 지정하고,
분류 허용 오차를 지정할 수 있다.
▶️ 안하면 계~속 가중치 업데이트함

📌 요약

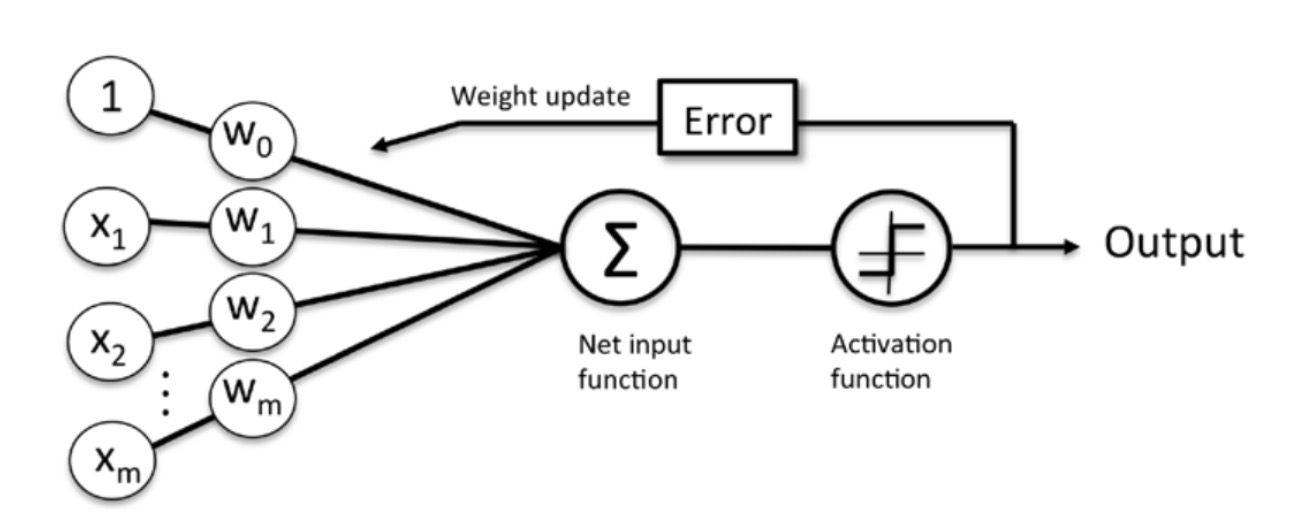
샘플 x를 입력으로 받아 가중치 w를 연결하여 최종 입력(Net input)을 계산!
최종 입력(Net input) -> 임계 함수(Activation function)로 전달,
샘플의 예측 클래스 레이블인 -1 또는 +1의 이진 출력
학습단계에서 이 출력을 사용해 예측 오차를 계산하고 가중치를 업데이트함