관계 데이터 연산

원하는 데이터를 얻기 위해 릴레이션에 필요한 처리 요구를 수행하는 것

종류

• 관계 대수
• 관계 해석

➡️ 기능과 표현력 측면에서 능력이 동등

관계 대수와 관계 해석의 역할

• 데이터 언어의 유용성을 검증하는 기준
• 관계 대수나 관계 해석으로 기술할 수 있는 모든 질의(query)를 기술할 수 있는 데이터 언어를 관계적으로 완전(relationally complete)하다고 판단함

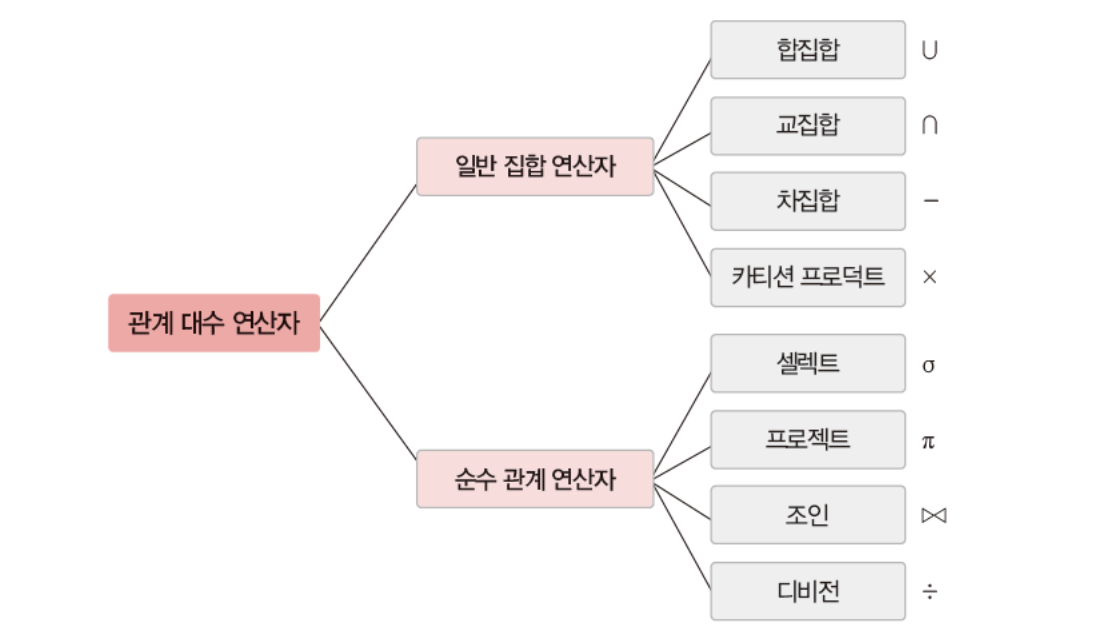
관계 대수

원하는 결과를 얻기 위해 릴레이션의 처리 과정을 순서대로 기술하는
언어

• 절차 언어
• 일반 집합 연산자와 순수 관계 연산자로 분류
• 폐쇄 특성(closure property)이 존재함
  • 피연산자도 릴레이션이고 연산의 결과도 릴레이션

연산자를 하나씩,,^^ 알아보도록 합시다..^^

Select Operation

릴레이션 R에서 셀렉션 조건식을 만족하는 투플만 선택해 반환!

예시)

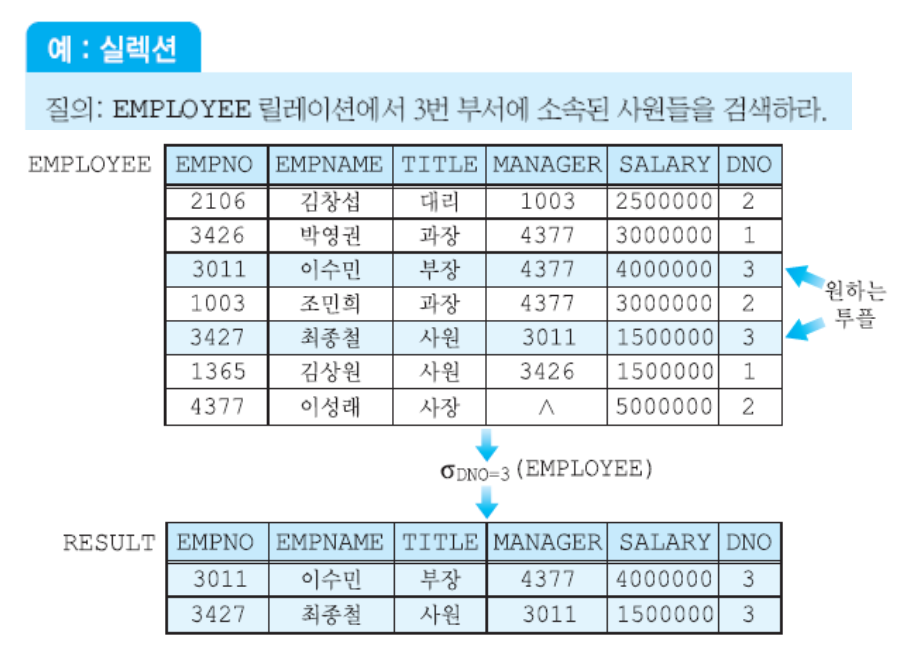
• 단항 연산자
• 하나의 릴레이션을 대상으로 연산을 수행
• 결과 릴레이션의 차수 == 입력 릴레이션의 차수
• 원래 릴레이션의 카디날리티 >= 결과 릴레이션의 카디날리티
• 셀렉션 조건을 predicate 프레디키트라고도 함
• 셀렉션 조건 : 임의의 애트리뷰트, 상수,
  비교 연산자( =, <>, <=, <, >=, > )
  부울 연산자( AND, OR, NOT )

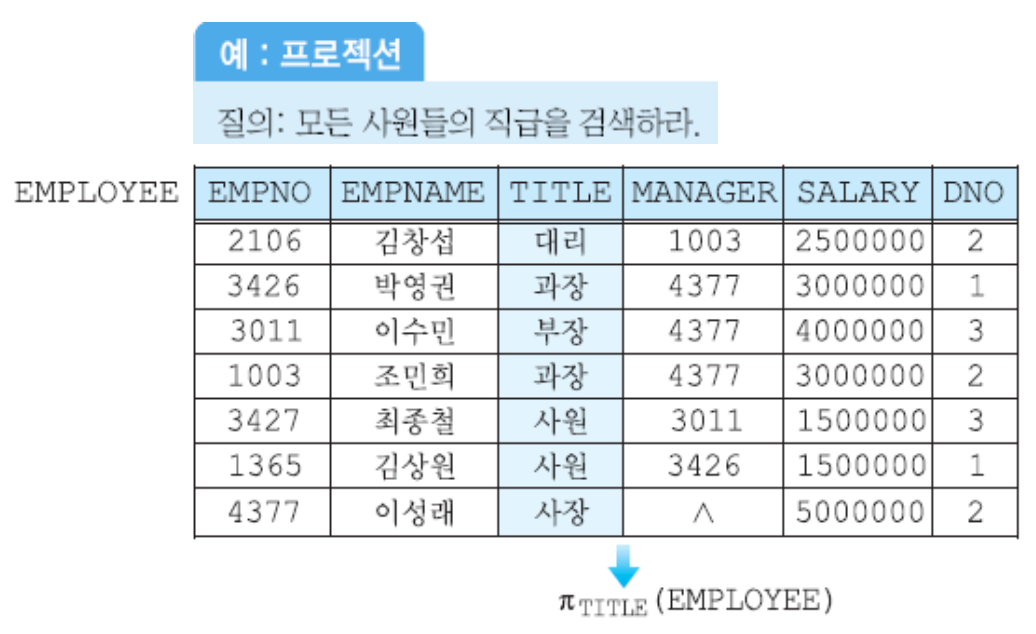
Project Operation

릴레이션 R에서 애트리뷰트 리스트에 나열된 애트리뷰트 값으로만 구성된 투플을 반환

• 하나의 릴레이션을 대상으로 연산을 수행
• 한 릴레이션의 애트리뷰트들의 부분 집합
• 결과 릴레이션은 <애트리뷰트 리스트>에 명시된 애트리뷰트들만 가짐
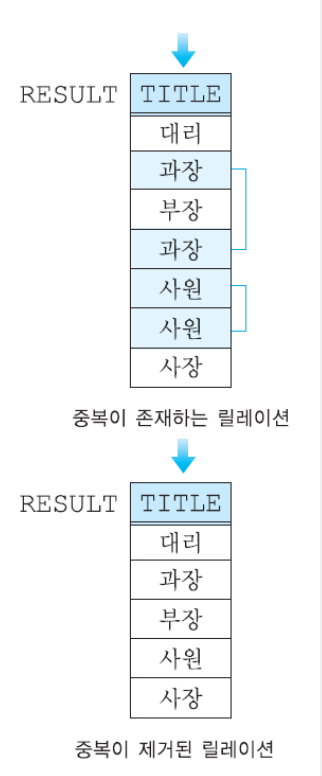
• 셀렉션의 결과 릴레이션에는 중복 투플이 존재할 수 없음.
  BUT 프로젝션 결과 릴레이션에는 중복된 투플 존재 가능!
• 예시!
  

일반 집합 연산자(set operation)

• 릴레이션이 투플의 집합이라는 개념을 이용하는 연산자

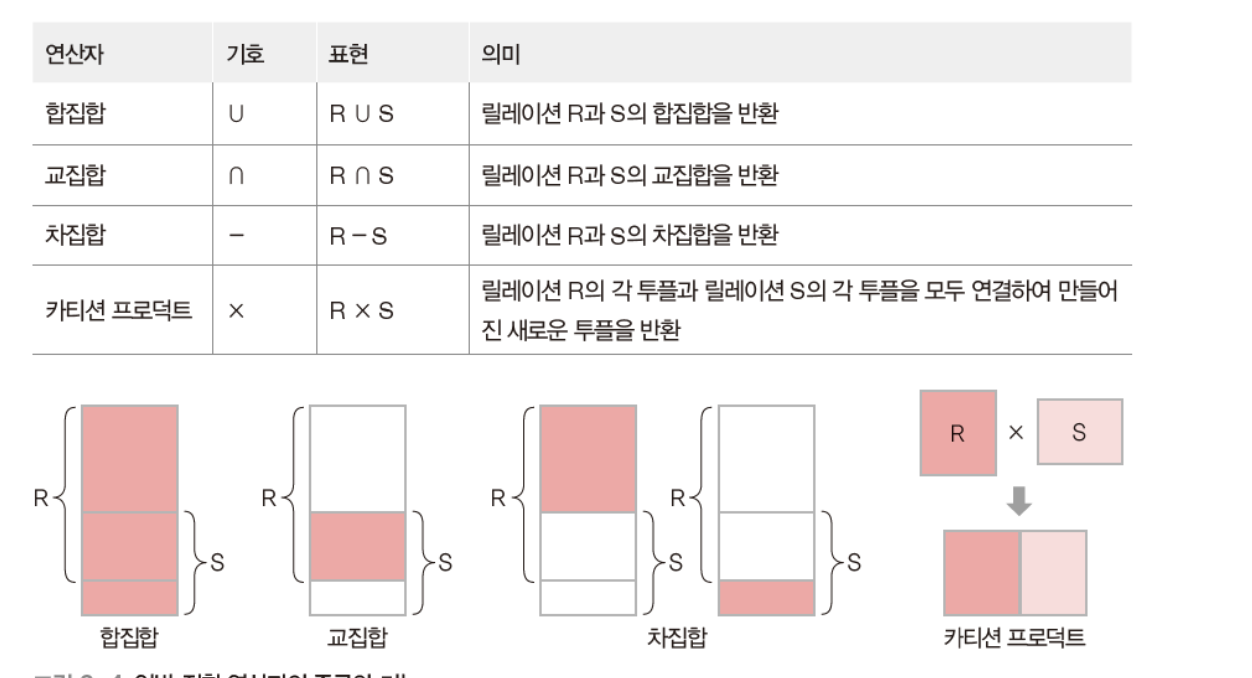
• 2개의 릴레이션을 대상으로 연산을 수행하기 때문에
  피연산자 2개 필요
  -합집합, 교집합, 차집합은 피연산자인 두 릴레이션이 합병 가능해야 함
  ➡️ 합병 가능 조건 :
  두 릴레이션의 차수가 같아야
  두 릴레이션에서 서로 대응되는 속성의 도메인이 같아야

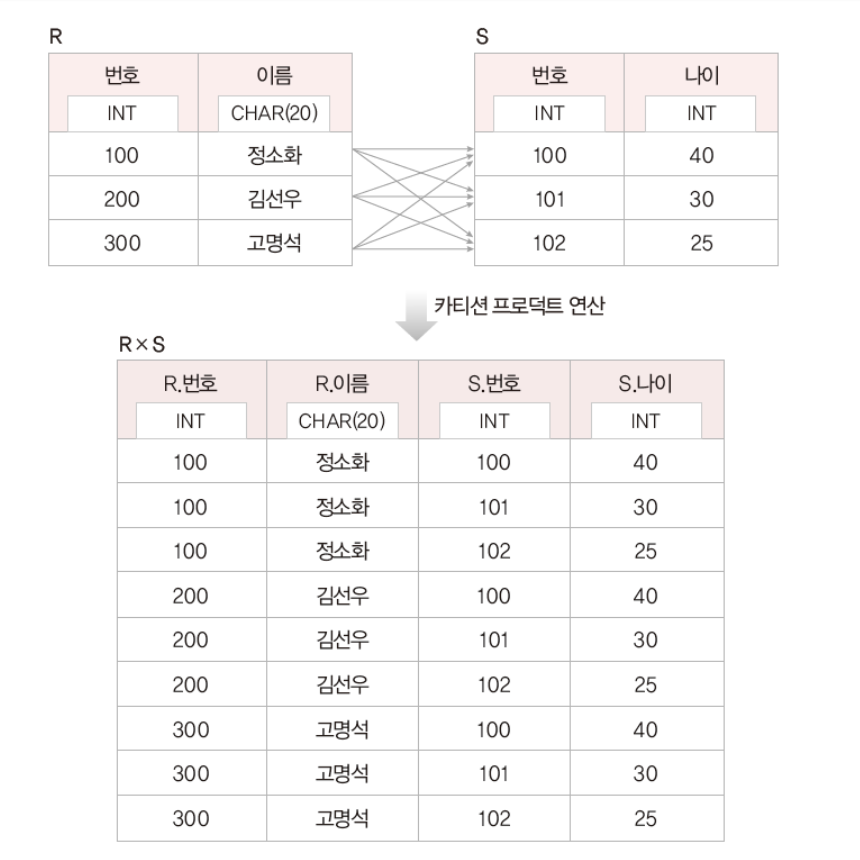
일반 집합 연산자 - cartesian product

두 릴레이션 R과 S의 카티션 프로덕트
R X S

• 결과 릴레이션의 특성
  • 차수 : 릴레이션R과 S의차수의 합
  • 카디널리티: 릴레이션 R과 S의 카디널리티의 곱
• 교환적 특징가
  R x S = S x R
• 결합적 특징
  • (R x S) x T = R x (S x T)
  

일반 집합 연산자 - Union Operation

합병 가능한 두 릴레이션 R과 S의 합집합
릴레이션 R에 속하거나 릴레이션 S에 속하는 모든 투플로 결과 릴레이션 구성
R ∪ S

• 결과 릴레이션의 특성
  • 차수는 릴레이션 R과 S의 차수와 같음
  • 카디널리티는 릴레이션 R과 S의 카디널리티를 더한 것과 같거나 적어짐
• 교환적 특징
  • R∪S = S∪R
• 결합적 특징
  • (R∪S)∪T = R∪(S∪T)

일반 집합 연산자 - Set-Intersection Operation

합병 가능한 두 릴레이션 R과 S의 교집합 R∩S
릴레이션 R과 S에 공통으로 속하는 투플로 결과 릴레이션 구성
R ∩ S

• 결과 릴레이션의 특성
  • 차수는 릴레이션 R과 S의 차수와 같음
  • 카디널리티는 릴레이션 R과 S의 어떤 카디널리티보다 크지 않음
• 교환적 특징
  • R∩S = S∩R
• 결합적 특징이 있음
  • (R∩S)∩T = R∩(S∩T)

일반 집합 연산자 - Set Difference Operation

합병 가능한 두 릴레이션 R과 S의 차집합
릴레이션 R에는 존재하지만 릴레이션 S에는 존재하지 않는 투플로 결과 릴레이션 구성
R – S

• 결과 릴레이션의 특성
  • 차수는 릴레이션 R과 S의 차수와 같음
  • R–S의 카디널리티는 릴레이션 R의 카디널리티와 같거나 적음
  • S–R의 카디널리티는 릴레이션 S의 카디널리티와 같거나 적음
• 교환적, 결합적 특징이 없음!

순수 관계 연산자(relational operation)

• 릴레이션의 구조와 특성을 이용하는 연산자
  

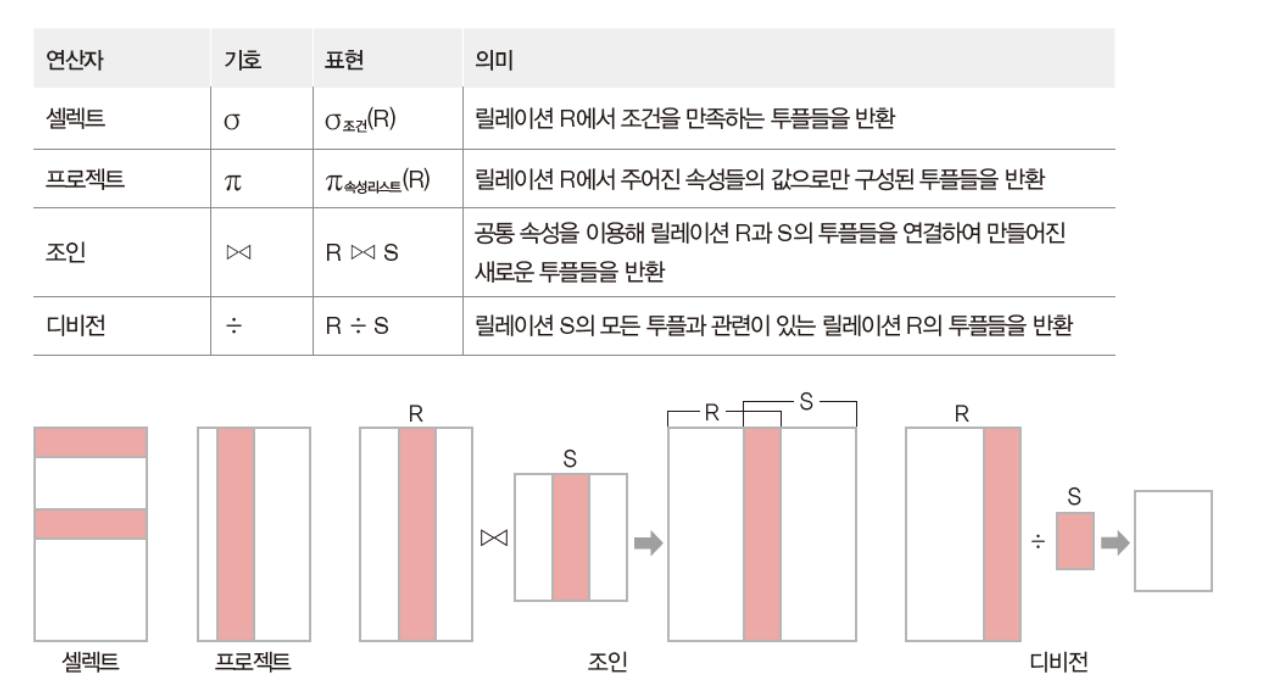
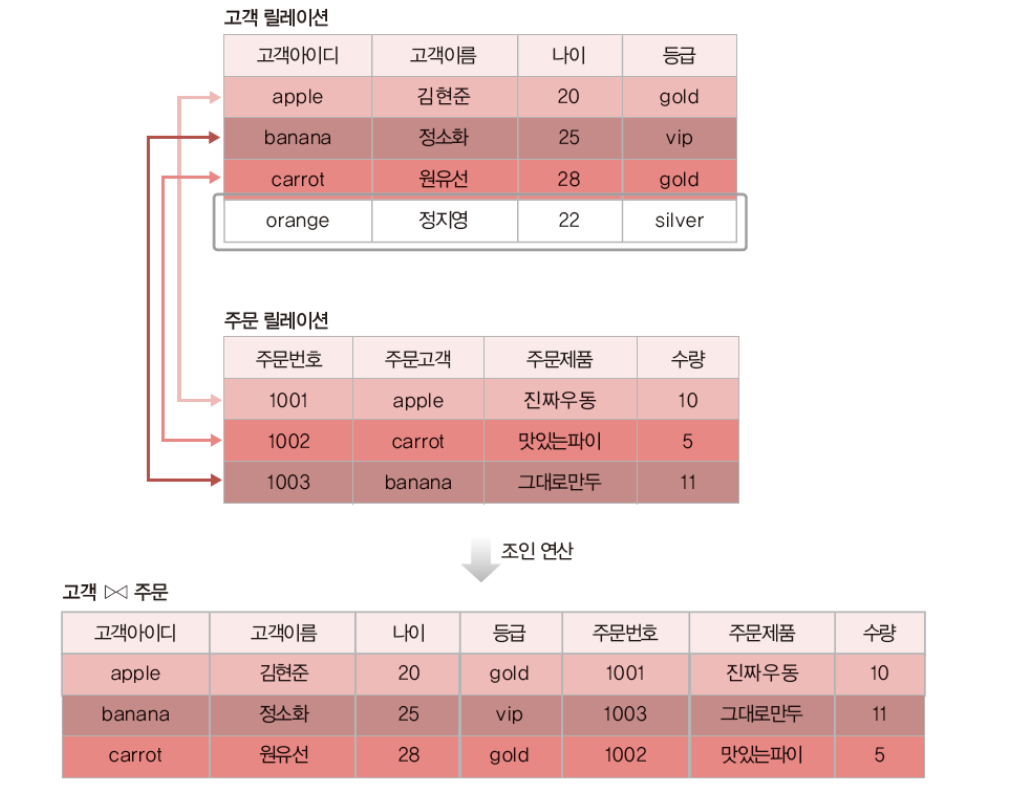
순수 관계 연산자 - Join Operation

조인 속성을 이용해 두 릴레이션을 조합하여 결과 릴레이션을 구성
릴레이션1 ⋈ 릴레이션2

자연 조인(natural join)

• 조인속성의 값이 같은 투플만 연결하여
  생성된 투플을 결과 릴레이션에 포함
  ✅ 조인속성 = 두 릴레이션이 공통으로 가지고 있는 속성
  

세타 조인(theta join, 𝜽-join)

주어진 조인 조건을 만족하는 두 릴레이션의 모든 투플을 연결하여 생성된 새로운 투플로 결과 릴레이션을 구성
릴레이션1 ⋈A𝜃B 릴레이션2

• 자연조인보다 더 일반화된 조인
• 결과 릴레이션의 차수 = 두 릴레이션의 차수 합
• 𝜽는 비교 연산자(>, ≥, <, ≤, =, ≠)를 의미

동일 조인(equi-join)

• 𝜽 연산자가 “=”인 세타 조인을 의미
  

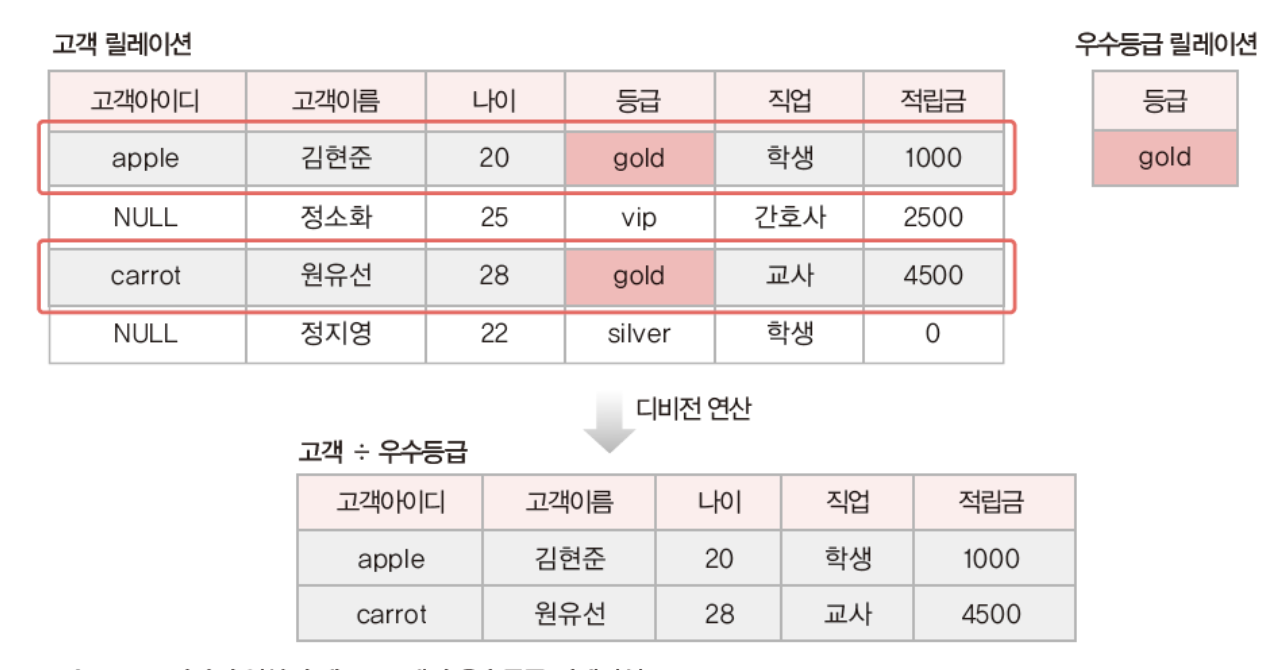
순수 관계 연산자 – 디비전(division)

릴레이션2의 모든 투플과 관련이 있는 릴레이션1의 투플로 결과 릴레이션을 구성
‼️ 단, 릴레이션1이 릴레이션2의 모든 속성을 포함하고 있어야(도메인이 같아야) 연산이 가능
릴레이션1 ÷ 릴레이션2

관계 해석

처리를 원하는 데이터가 무엇인지만 기술하는 언어

• 비절차 언어(nonprocedural language)
• 수학의 프레디킷 해석(predicate calculus)에 기반

분류

• 투플 관계 해석(tuple relational calculus)
• 도메인 관계 해석(domain relational calculus)