밑바닥부터 시작하는 딥러닝2 - 2장

jLica·2023년 7월 2일

밑바닥부터 시작하는 딥러닝2

목록 보기

1/7

2장 - 자연어와 단어의 분산 표현

자연어 처리가 다루는 분야는 다양하지만, 그 본질적 문제는 컴퓨터가 우리의 말을 알아듣게(이해하게) 만드는 것이다. 이번 장은 컴퓨터에 말을 이해시킨다는 게 무슨 뜻인지, 그리고 어떤 방법들이 존재하는지를 중심으로 살펴보고자 한다.

2.1 - 자연어 처리란

한국어와 영어 등 우리가 평소에 쓰는 말을 자연어 $^{natural \space language}$ 라 한다.

그러니 자연어 처리 $^{Natural \space Language \space Processing}(\bold{ NLP})$ 를 문자 그대로 해석하면 자연어를 처리하는 분야이고, 알기 쉽게 풀어보면 '우리의 말을 컴퓨터에 이해시키기 위한 기술(분야)'이다.

2.1.1 - 단어의 의미

우리의 말은 '문자'로 구성되며, 말의 의미는 '단어'로 구성된다. 말하자면 단어가 의미의 최소 단위인 셈이다. 그래서 컴퓨터에 자연어를 이해시키려면 무엇보다 '단어의 의미'를 이해시키는 게 중요하다.

이번 장의 주제는 컴퓨터에 '단어의 의미' 이해시키기이다. 이를 위해 '단어의 의미'를 잘 파악하는 표현 방법에 관해 생각해 본다. 구체적으로는 이번 장과 다음 장에서 세 가지 기법을 살펴본다.

시소러스를 활용한 기법 (이번 장)
통계 기반 기법 (이번 장)
추론 기반 기법(word2vec) (다음 장)

2.2 - 시소러스

시소러스란 (기본적으로는) 유의어 사전으로, 동의어나 유의어가 한 그룹으로 분류되어 있다.

또한 자연어 처리에 이용되는 시소러스에서는 단어 사이의 '상위와 하위' 혹은 '전체와 부분' 등, 더 세부적인 관계까지 정의해 둔 경우가 있다.

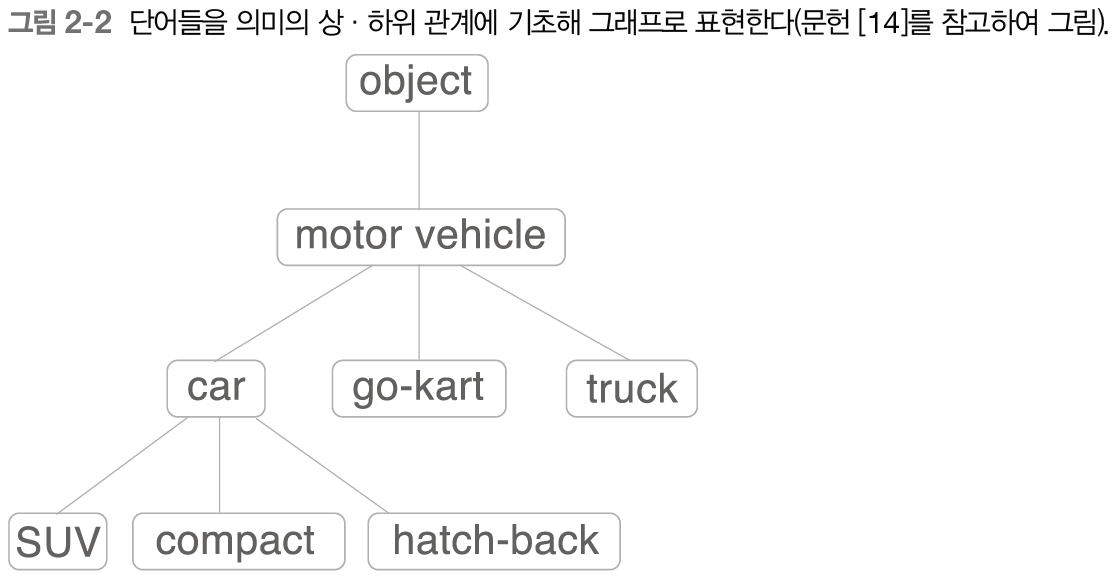
이처럼 모든 단어에 대한 유의어 집합을 만들고, 단어들의 관계를 그래프로 표현하여 단어 사이의 연결을 정의할 수 있다.

2.2.2 - 시소러스의 문제점

시소러스에는 수많은 단어에 대한 동의어와 계층 구조 등의 관계가 정의돼 있다. 그런데 이걸 수작업으로 레이블링하는 방식에는 큰 결점이 존재한다. 다음은 시소러스 방식의 대표적인 문제점들이다.

시대 변화에 대응하기 어렵다.
우리가 사용하는 말은 계속 변화한다. 새로 생겨나고, 낡은 말은 잊혀진다. 이런 단어의 변화에 대응하려면 일일이 수작업으로 갱신해야 한다.
사람을 쓰는 비용은 크다.
시소러스를 만드는 데 엄청난 인건비가 든다. 세상에 존재하는 수많은 단어들의 관계를 수작업으로 정의하려면, 엄청난 대작업이 될 것이다.
단어의 미묘한 차이를 표현할 수 없다.
시소러스에서는 뜻이 비슷한 단어들을 묶는다. 그러나, 비슷한 단어들이라도 미묘하게 차이가 있는 법이다. 시소러스는 미묘한 차이를 표현할 수 없고, 표현하려 한다면 엄청난 대작업이 될 것이다.

이 문제를 피하기 위해, '통계 기반 기법'과 신경망을 사용한 '추론 기반 기법'을 알아볼 것이다. 이 두 기법에서는 대량의 텍스트 데이터로부터 '단어의 의미'를 자동으로 추출한다.

딥러닝이 실용화되면서 사람이 개입할 필요가 줄어들었다. 사람의 개입을 최소로 줄이고 텍스트 데이터만으로 원하는 결과를 얻어내는 방향으로 패러다임이 바뀌고 있다.

2.3 - 통계 기반 기법

통계 기반 기법을 살펴보면서 말뭉치 $^{corpus}$ 를 이용할 것이다. corpus란 간단히 말하면 대량의 텍스트 데이터이다. 다만, 일반적으로 자연어 처리 연구 등을 목적으로 수집된 텍스트 데이터를 corpus라 일컫는다.

결국 corpus란 텍스트 데이터에 지나지 않지만, 자연어에 대한 사람의 '지식'이 충분히 담겨 있다고 생각할 수 있다. 문장을 쓰는 방법, 단어를 선택하는 방법, 단어의 의미 등 자연어에 대한 지식이 포함되어 있다.

통계 기반 기법의 목표는 이러한 corpus에서 자동으로, 그리고 효율적으로 핵심을 추출하는 것이다.

2.3.1 - 파이썬으로 말뭉치 전처리하기

우선 매우 작은 텍스트 데이터(corpus)에 전처리 $^{preprocessing}$ 를 해보자. 여기서 말하는 전처리란 텍스트 데이터를 단어로 분할하고 그 분할된 단어들을 단어 ID 목록으로 변환하는 일이다.

우선 이번 corpus로 이용할 예시 문장부터 보자.

text = 'You say goodbye and I say hello.'

실전이라면 이 text 변수에 수천, 수만 개가 넘는 문장이 연이어 담겨 있을 것이다. 하지만 지금은 설명이 쉽도록 작은 텍스트 데이터로 전처리를 수행한다. 이제 이 text 변수를 단어 단위로 분할해 보자.

text = text.lower()
text = text.replace('.', ' .') #You say goodbye and I say hello .
words = text.split(' ')
print(words) #['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello', '.']

문장 첫머리의 대문자로 시작하는 단어도 소문자 단어와 똑같이 취급하기 위해 lower() 메서드를 사용했다. 그리고 공백을 기준으로 분할하기 위해 문장 끝의 마침표 앞에 공백을 넣어 주었다.

단어 단위로 분할하여 다루기 쉬워지긴 했는데, 그래도 텍스트 그대로 조작하기는 여러모로 불편하다. 그래서 단어에 ID를 부여하고, ID의 리스트로 이용할 수 있도록 손질한다.

word_to_id = {}
id_to_word = {}

for word in words:
  if word not in word_to_id:
    new_id = len(word_to_id)
    word_to_id[word] = new_id
    id_to_word[new_id] = word

word_to_id에 없는 단어는 배열 길이에 따라 0부터 순차적으로 ID가 부여된다.

이로써 ID와 단어의 대응표가 만들어졌다. 그렇다면 실제로 어떤 내용이 담겨 있는지 보자.

print(id_to_word) #{0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}
print(word_to_id) #{'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6}

단어 목록을 단어 ID 목록으로 변경해 보자.

import numpy as np
corpus = [word_to_id[w] for w in words]
corpus = np.array(corpus)
print(corpus) #[0 1 2 3 4 1 5 6]

이상으로 corpus 전처리가 끝났다. 텍스트 상태일 때보다 ID로 치환한 생태가 컴퓨터에게는 더 익숙하겠다.

2.3.2 - 단어의 분산 표현

뜬금없지만, RGB 표현 방식은 색을 3차원 벡터로 표현한다. 모든 색을 단 3개의 성분으로 간결하게 표현할 수 있고, 대충 어떤 색인지 짐작하기도 쉽다.

색을 벡터로 표현함으로써 얻을 수 있는 이점이 한두 가지가 아니다. 그렇다면 '단어'도 벡터로 표현할 수 있을까? 이제부터 우리가 원하는 것은 '단어의 의미'를 정확하게 파악할 수 있는 벡터 표현이다. 이를 자연어 처리 분야에서는 단어의 분산 표현 $^{distributional \space representation}$ 이라고 한다.

2.3.3 - 분포 가설

분포 가설 $^{distributional \space hypothesis}$ 이란 '단어의 의미는 주변 단어에 의해 형성된다'는 아이디어이다.

분포 가설이 말하고자 하는 바는 간단하다. 단어 자체에는 의미가 없고, 그 단어가 사용된 '맥락 $^{context}$ '이 의미를 형성한다는 것이다.

앞으로 '맥락'이라는 단어를 자주 사용할 것이다. 이번 장에서 '맥락'이라 하면 주목하는 단어의 주변에 놓인 단어를 가리킨다.

여기서는 좌우 두 단어씩이 '맥락'에 해당한다. 그리고 맥락의 크기, 즉 주변 단어를 몇 개나 포함할지를 '윈도우 크기 $^{window \space size}$ '라고 한다. 윈도우 크기가 1이면 좌우 한 단어씩, 윈도우 크기가 2면 좌우 두 단어씩이 맥락에 포함된다.

여기서는 좌우로 같은 수의 단어를 맥락으로 사용했다. 하지만 상황에 따라서 왼쪽 단어, 혹은 오른쪽 단어만을 사용하기도 하고, 문장의 시작과 끝을 고려할 수도 있다.

2.3.4 - 동시발생 행렬

분포 가설에 기초해 단어를 벡터로 나타내는 방법을 생각해 보자. 주변 단어를 세 보는 방법이 자연스럽게 떠오를 것이다. 어떤 단어에 주목했을 때, 그 주변에 어떤 단어가 몇 번이나 등장하는지를 세어 집계하는 것이다. 이 책에서는 이를 '통계 기반' 기법이라고 부른다.

그럼 이전에 나온 예시 문장으로 통계 기반 기법을 살펴보자.

윈도우의 크기를 1로 했을 때, "you"의 맥락은 "say" 하나뿐이다. 이를 표로 정리하면 다음과 같다.

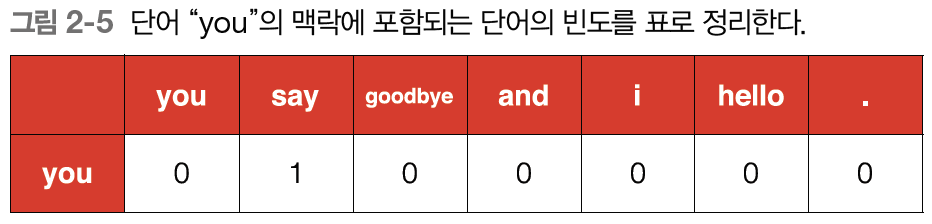
이 그림은 "you"의 맥락으로써 동시에 발생(등장)하는 단어의 빈도를 나타낸 것이다. 그리고 이를 바탕으로 "you"라는 단어를 벡터로 표현할 수 있게 됐다. 바로 [0, 1, 0, 0, 0, 0, 0] 말이다.

계속해서 "say"에 대해서도 같은 작업을 수행해보자.

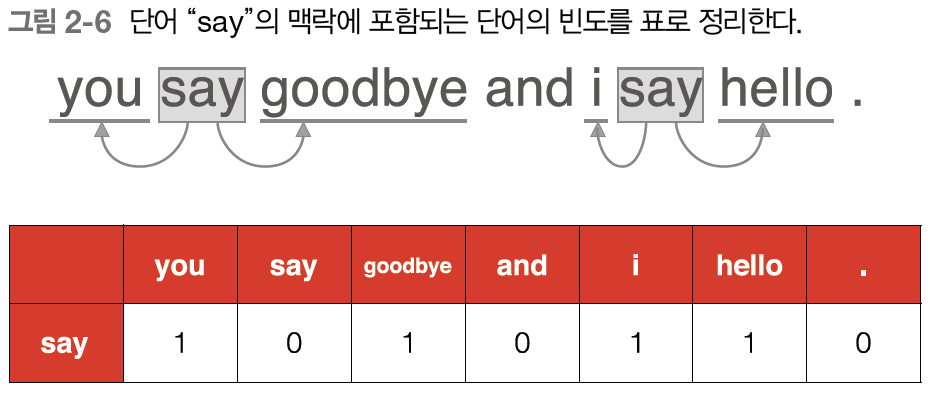
이 결과로부터 "say"라는 단어는 벡터 [1, 0, 1, 0, 1, 1, 0]으로 표현할 수 있겠다. 이상의 작업을 모든 단어에 대해 수행한 결과는 다음과 같다.

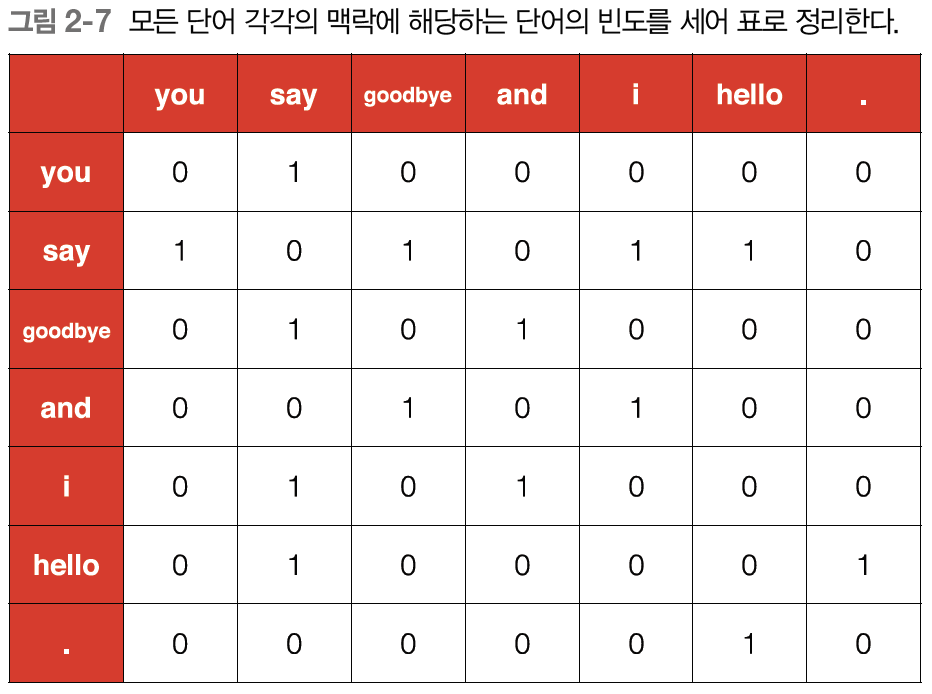
이 표가 행렬의 형태를 띤다는 뜻에서 동시발생 행렬 $^{co-occurrence \space matrix}$ 이라고 한다. 이 표의 각 행은 해당 단어를 표현한 벡터가 된다.

2.3.5 - 벡터 간 유사도

벡터 사이의 유사도를 측정하는 방법은 다양하다. 대표적으로는 벡터의 내적이나 유클리드 거리 등을 꼽을 수 있겠다. 그 외에도 다양하지만, 단어 벡터의 유사도를 나타낼 때는 코사인 유사도 $^{cosine \space similarity}$ 를 자주 이용한다.

두 벡터 $\bold x = (x_1, \space x_2, \space, x_3, \space \cdots, \space x_n)$ 과 $\bold y = (y_1, \space y_2, \space, y_3, \space \cdots, \space y_n)$ 이 있다면, 코사인 유사도는 다음과 같이 정의된다.

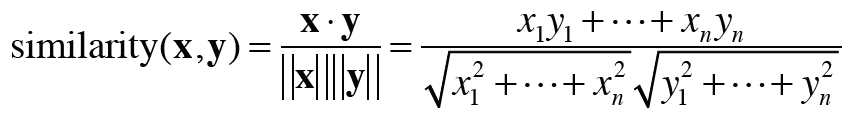
분자에는 벡터의 내적이, 분모에는 각 벡터의 노름 $^{norm}$ 이 등장한다. 노름은 벡터의 크기를 나타낸 것으로, 여기서는 L2 노름을 계산한다.

그런데 이 식, 벡터의 내적에서 $cos \theta$ 를 구하는 공식과 일치한다. 사실 코사인 유사도의 직관적인 의미가 바로 '두 벡터가 가리키는 방향이 얼마나 비슷한가'이다.

두 벡터의 방향이 얼마나 일치하는지는 $cos \theta$ 로 알 수 있다. $cos \theta$ 는 방향이 완전히 같을 때 1이고, 180 $\degree$ 다를 때 -1이 되기 때문이다.

2.4 - 통계 기반 기법 개선하기

앞 절에서 동시발생 행렬을 만들고, 이를 이용해 단어를 벡터로 표현하는 데는 성공했다. 하지만, 아직 개선할 점이 있다.

2.4.1 - 상호정보량

앞 절에서 본 동시발생 행렬의 원소는 두 단어가 동시에 발생한 횟수를 나타낸다. 사실 이 '발생' 횟수라는 게 그리 좋은 특징이 아니다.

예를 들어 corpus에서 "the"와 "car"의 동시발생을 생각해 보자. 분명 "... the car ..."라는 문구가 자주 보일 것이므로 두 단어의 동시발생 횟수는 아주 많겠다.

한편, "car"와 "drive"는 확실히 관련이 깊다. 하지만, 단순히 등장 횟수만 보면 "car"는 "drive"보다는 "the"와의 관련성이 훨씬 강하다고 나올 것이다.

이 문제를 해결하기 위해 점별 상호정보량 $^{Pointwise \space Mutual \space Information}$ (PMI)이라는 척도를 사용한다. PMI는 확률 변수 $x$ 와 $y$ 에 대해 다음 식으로 정의된다.

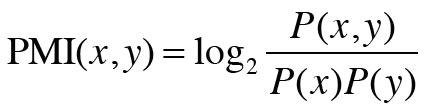
위 식에서 $P(x)$ 는 $x$ 가 일어날 확률, $P(y)$ 는 $y$ 가 일어날 확률, $P(x, y)$ 는 $x$ 와 $y$ 가 동시에 일어날 확률이다. 이 PMI 값이 높을수록 관련성이 높다는 뜻이다.

이 식을 동시발생 행렬을 사용할 수 있도록 조금 바꿔 보자. $P(x)$ , 즉 $x$ 가 일어날 확률이라는 뜻은 corpus 중에서 $x$ 라는 단어가 등장할 확률이라고 볼 수 있다. 식으로 나타내려면, $x$ 의 등장 횟수를 corpus에 포함된 단어의 수로 나눠주면 된다.

동시발생 행렬을 $C$
단어 $x$ 와 $y$ 가 동시발생하는 횟수를 $C(x, \space y)$
단어 $x$ 와 $y$ 의 등장 횟수를 각각 $C(x)$ , $C(y)$
마지막으로, corpus에 포함된 단어의 수를 $N$ 이라 한다.

새로 추가한 문자들로 식을 바꿔보면 다음과 같다.

그런데 이 PMI에도 문제가 하나 있는데, 바로 두 단어의 동시발생 횟수가 0이면 $log_20 = -\infty$ 가 된다는 점이다. 이 문제를 피하기 위해 실제로 구현할 때는 양의 상호정보량 $^{Positive \space PMI}$ (PPMI)을 사용한다.

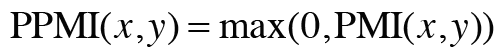
이 식에 따라 PMI가 음수일 때는 0으로 취급한다.

2.4.2 - 차원 감소

demensionality reduction, 중요한 정보를 최대한 유지하면서 벡터의 차원을 줄이는 방법이다.

원소 대부분이 0인 행렬 또는 벡터를 희소 $^{sparse}$ 행렬 또는 벡터라고 한다. 차원 감소의 핵심은 이 희소벡터를 원소 대부분이 0이 아닌 값으로 구성된 밀집벡터로 변환하는 것이다.

차원을 감소시키는 방법 중, 특잇값분해 $^{Singular \space Value \space Decomposition}$ (SVD)를 알아보자. SVD는 임의의 행렬을 세 행렬의 곱으로 분해하는데, 수식은 다음과 같다.

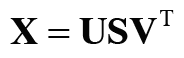
SVD는 임의의 행렬 $\bold X$ 를 $\bold U$ , $\bold S$ , $\bold V$ 라는 세 행렬의 곱으로 분해한다.

여기서 $\bold U$ 와 $\bold V$ 는 각각 직교행렬이고, 그 열벡터는 서로 직교한다. 또한 $\bold S$ 는 대각행렬, 즉 대각성분 외에는 모두 0인 행렬이다.

위에 언급했듯 $\bold U$ 는 직교행렬이다. 그리고 이 직교행렬은 어떠한 공간의 축(기저)을 형성한다. 지금 우리의 맥락에서는 이 $\bold U$ 행렬을 '단어 공간'으로 취급할 수 있다. 또한 $\bold S$ 는 대각 행렬로, 그 대각성분에는
'특잇값 $^{singular \space value}$ '이 큰 순서로 나열돼 있다.

특잇값이란, 쉽게 말해 '해당 축'의 중요도라고 간주할 수 있다. 그래서 다음과 같이 중요도가 낮은 원소, 즉 특잇값이 작은 원소를 깎아내는 방법을 생각할 수 있다.

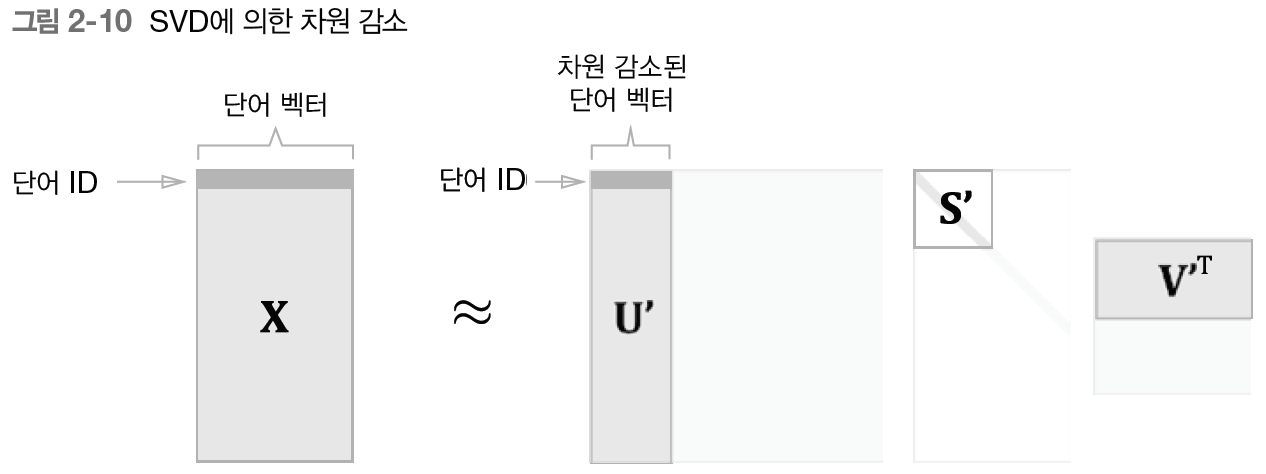
행렬 $\bold S$ 에서 특잇값이 작다면 중요도가 낮다는 뜻이므로, 행렬 $\bold U$ 에서 여분의 열벡터를 깎아내어 원래의 행렬을 근사할 수 있다. 이를 PPMI 행렬에 적용해 보자. 그러면 행렬 $\bold X$ 의 각 행에는 해당 단어 ID의 단어 벡터가 저장되어 있으며, 그 단어 벡터가 행렬 $\bold U'$ 라는 차원 감소된 벡터로 표현되는 것이다.

jLica

초보입니다.

다음 포스트

밑바닥부터 시작하는 딥러닝2 - 2장