최대 가능도 추정법 MLE(Maximum Likelihood Estimation)

MLE(Maximum Likelihood Estimation)

MLE

• 이론적으로 가장 가능성이 높은 모수를 추정하는 방법
  그냥 특정 sample들 중에서 가장 모수를 잘 나타낼 수 있는 최대 값을 찾는 거?

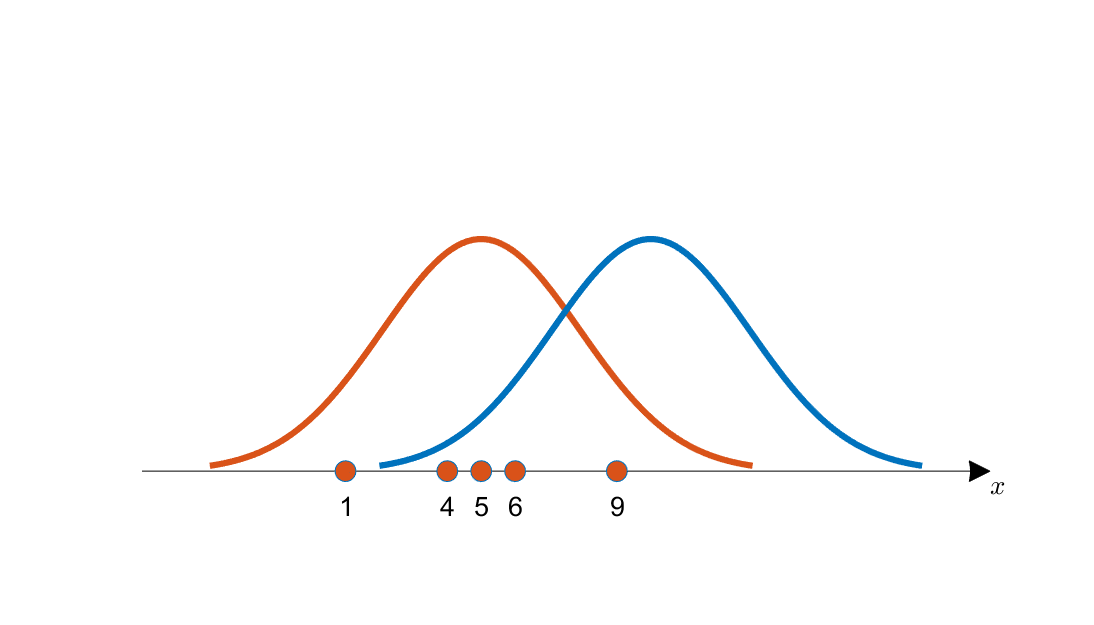
눈으로 보기에도 파란색 곡선 보다는 주황색 곡선에서 이 데이터들을 얻었을 가능성이 더 커보인다.

왜냐면 획득한 데이터들의 분포가 주황색 곡선의 중심에 더 일치하는 것 처럼 보이기 때문이다.

이 예시를 보면, 우리가 데이터를 관찰함으로써 이 데이터가 추출되었을 것으로 생각되는 분포의 특성을 추정할 수 있음을 알 수 있다. 여기서는 추출된 분포가 정규분포라고 가정했고, 우리는 분포의 특성 중 평균을 추정하려고 했다.
<출처 : https://angeloyeo.github.io/2020/07/17/MLE.html>

연속형 확률변수 / 이산형 확률변수의 차이를 제외하곤 둘이 같음

가능도 함수
모수 $\theta$를 따르는 분포가 data $X$를 관찰할 가능성 (확률이 아니다!)
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$-> ($\theta$에 대한 적분이 1이 아닐 수 있다는 의미!)

데이터 집합 x가 독립적으로 추출 되었을 경우 로그 가능도로 최적화

-> 로그를 통해 곱셈 계산식을 덧셈 계산식으로 치환

로그 가능도를 취하는 이유!?
사실 L이나 log L이나 모두 MLE이지만 데이터의 숫자가 너무 많아지면 가능도를 계산하는 것이 불가능
=> 연산량을 $O(n^2)$에서 $O(n)$으로 줄여줌

대부분의 손실함수에서 경사하강법을 사용하기 때문에 negative log likelihood로 최적화하게 된다

MLE Example
정규분포를 따르는 확률변수 $X$로부터 독립적인 표본 $\{x_{1},...,x_{n}\}$을 얻었을 때 MLE를 통해 모수를 추정하면?

※MLE는 불편 추정량을 보장하지 않는다

<참고>

• 부스트캠프 AI Tech 교육자료