(AI Math)경사하강법 알고리즘

꼼댕이·2022년 9월 20일

1주차 ai math

경사 하강법

목록 보기

1/2

1. 미분과 경사하강법

1.1 경사하강법 (gradient descent)

backpropagation을 수행하며 cost function에 대한 편미분을 통해 최적의 w와 b를 구해 전체적인 모델의 파라미터를 재구성

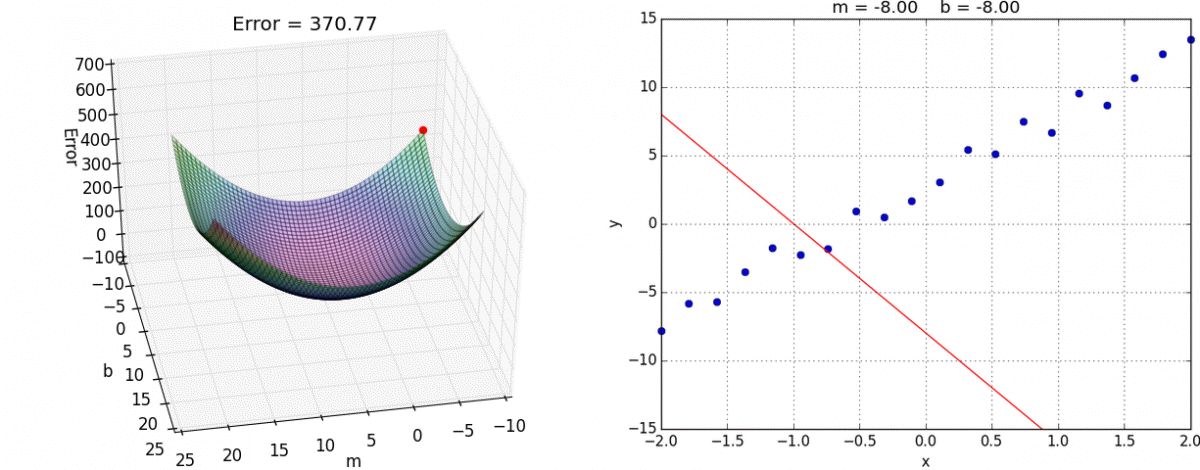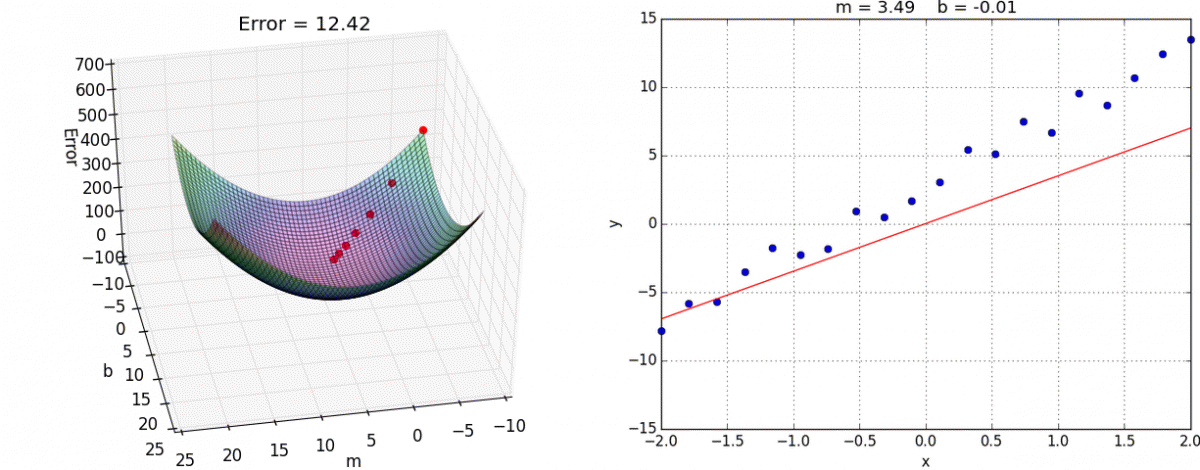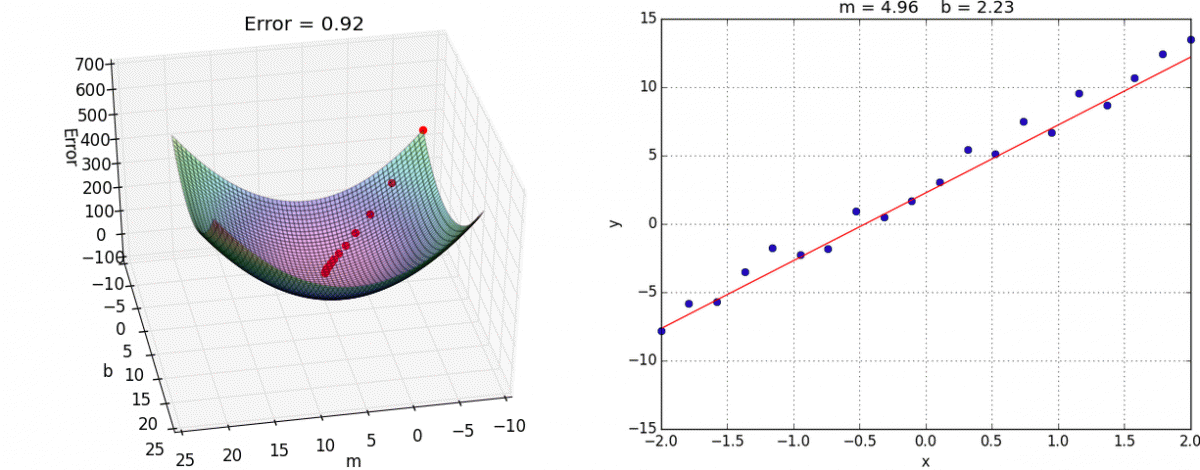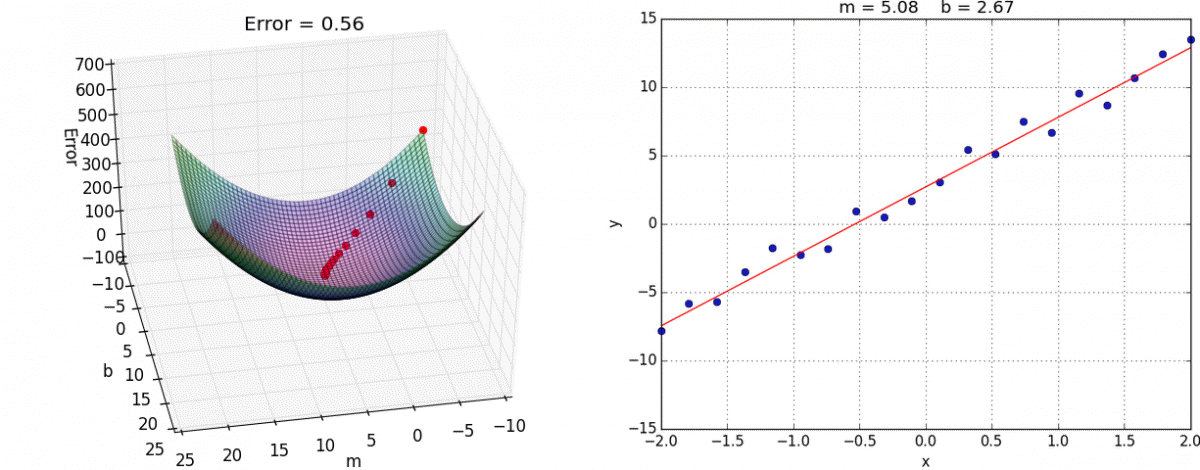
장점 : 모델의 최적화된 파라미터를 기반으로 학습 가능

단점 : local minimum 문제에 빠지기 쉬움 (뒤에 나오는 SGD를 통해 어느정도 해결 가능)

1.2 gradient 함수

함수 생성은 동일 (sympy library 활용)
(SymPy: 수학 방정식의 기호(symbol)를 사용하게 해 주는 라이브러리)

def func(val):
    fun = sym.poly(x**2 + 2*x + 1)
    return fun.subs(x, val), fun

gradient 함수 방법1) 기본 미분식을 그대로 사용
h만큼 움직였을 때 변화율을 구해주는 함수

f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}

def gradient(f, x, h=1e-9):
	result = (f(x+h) - f(x)) / h
	return result

gradient 함수 방법2) sympy library 활용

def gradient(fun, val):
   diff = sym.diff(fun(val)[1])
   return diff.subs(x, val), diff

1.2.1 입력값이 scalar 일 때 Gradient Descent

Pseudo Code

gradient : 미분 계산 함수
init : 시작점
lr : 학습률
eps (epsilon) : 알고리즘 종료조건

val = init
grad = gradient(val)
while (abs(grad) > eps):
	val = val - lr * grad
    grad = gradient(val)

미분(differentiation)
- 변수의 움직임에 따른 함수값의 변화량을 측정하기 위한 도구로써 최적화에서 제일 많이 사용하는 기법 -

편미분(partial differentiation)
- 벡터가 입력인 다변수 함수의 경우 사용 -
- 각 변수별로 편미분을 계산한 gradient vector를 이용해서 gradient ascent/descent에 사용! -

\partial x_{i}f(x) = \lim_{h\to\ 0} {f(x+he_{i}) - f(x)\over h}

\nabla f = (\partial x_{1}f, \partial x_{2}f, ... ,\partial x_{d}f)

앞에서 사용한 미분값인 $f'(x)$ 대신에 $\nabla f$ (gradient vector)를 사용하여 변수 $x = (x_{1}, ... , x_{d})$ 를 한번에 업데이트 가능하다!

Gradient Vector

$f(x,y) = x^2+2y^2$
$-\nabla f= -(2x,4y)$

-gradient f = 극소점으로 간다!

1.2.2 입력값이 vector 일 때 Gradient Descent

Pseudo Code

gradient : 미분 계산 함수
init : 시작점
lr : 학습률
eps (epsilon) : 알고리즘 종료조건

val = init
grad = gradient(val)
while (norm(grad) > eps):
	val = val - lr * grad
    grad = gradient(val)

경사하강법 알고리즘은 그대로 적용하지만 벡터일 땐 절댓값 대신 norm을 계산!

2.선형회귀 (Linear Regressoion)

2.1 선형회귀 목적식 (cost, loss)

선형회귀 목적식 : $\Vert y-x\beta \Vert_{2}$
이를 최소화하는 $\beta$ 를 찾아야 하므로 gradient vector를 구해야 한다!

\nabla _{\beta} \Vert y-x\beta \Vert_{2}\ =\ (\partial \beta_{1}\Vert y-x\beta \Vert_{2} \cdots \partial \beta_{d}\Vert y-x\beta \Vert_{2})

\partial \beta_{k}\Vert y-x\beta \Vert_{2}\ =\ \partial \beta_{k}\{{1\over n}\sum{_{j=1}^dX_{i,j}\beta_{i,j} }\}^{1\over2}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ = -{X^Tk(y-X\beta) \over n\Vert y-X\beta \Vert_{2}}

목적식을 최소화하는 $\beta$ 를 구하는 경사하강법 알고리즘

\beta^{(t+1)} = \beta^t - \lambda\nabla_{\beta}\Vert y-X\beta^t \Vert

$\lambda$ = learning rate

Linear Regression Base 코드

train_x = (np.random.rand(1000) - 0.5) * 10
train_y = np.zeros_like(train_x)

def func(val):
    fun = sym.poly(7*x + 2)
    return fun.subs(x, val)

for i in range(1000):
    train_y[i] = func(train_x[i])

# initialize
w, b = 0.0, 0.0

lr_rate = 1e-2
n_data = len(train_x)
errors = []

for i in range(100):
    # 예측값 y
    _y = w * train_x + b

    # gradient
    gradient_w = ((_y - train_y) * train_x).mean()
    gradient_b = (_y - train_y).mean()

    # w, b update with gradient and learning rate
    w = w - lr_rate * gradient_w
    b = b - lr_rate * gradient_b

    # L2 norm과 np_sum 함수 활용해서 error 정의
    error = ((_y - train_y)**2).mean()
    # Error graph 출력하기 위한 부분
    errors.append(error)

print("w : {} / b : {} / error : {}".format(w, b, error))

Linear Regression More Complicated Function

y = w_0x_0 + w_1x_1 + w_2x_2 + b \\ y = x_0 + 3x_1 + 5x_2 + 7

for t in range(T):
	error = y - x @ B  # @는 행렬곱(matmul)
    grad = -transpose(x) @ error
    B = B - lr * grad

전체 코드 (Linear Regression More Complicated Function)

train_x = np.array([[1,1,1], [1,1,2], [1,2,2], [2,2,3], [2,3,3], [1,2,3]])
train_y = np.dot(train_x, np.array([1,3,5])) + 7

# random initialize
beta_gd = [9.4, 10.6, -3.7, -1.2]
# for constant element
expand_x = np.array([np.append(x, [1]) for x in train_x])

for t in range(5000):
    ## Todo
    error = train_y - expand_x @ beta_gd
    grad = -np.transpose(expand_x) @ error
    beta_gd = beta_gd - lr_rate * grad


print("After gradient descent, beta_gd : {}".format(beta_gd))

2.2 확률적 경사하강법 (SGD)

확률적 경사하강법 (Stochastic Gradient Descent)

데이터를 일부만 활용해서 update -> mini-batch
경사 하강법과 달리 최적화된 값을 찾을 수 있음!

mini-batch를 통해 일부분들을 기반으로 여러 곳에서의 minima(구덩이 부분)에 대한 gradient descent를 진행하다보니 local minima에 빠지는 단점을 어느정도 보완해줄 수 있다.

train_size = train_x.shape[0]
batch_size = 100

for i in range(100):
    batch_mask = np.random.choice(train_size, batch_size, replace=False)
    x_batch = train_x[batch_mask]
    y_batch = train_y[batch_mask]

전체 코드 (Linear Regression SGD)

train_x = (np.random.rand(1000) - 0.5) * 10
train_y = np.zeros_like(train_x)

def func(val):
    fun = sym.poly(7*x + 2)
    return fun.subs(x, val)

for i in range(1000):
    train_y[i] = func(train_x[i])

# initialize
w, b = 0.0, 0.0

lr_rate = 1e-2
n_data = 10
errors = []

train_size = train_x.shape[0]
batch_size = 100

for i in range(100):
    batch_mask = np.random.choice(train_size, batch_size, replace=False)
    x_batch = train_x[batch_mask]
    y_batch = train_y[batch_mask]

    _y = w * x_batch  + b

    gradient_w = ((_y - y_batch) * x_batch).mean()
    gradient_b = (_y - y_batch).mean()

    w = w - lr_rate * gradient_w
    b = b - lr_rate * gradient_b

    # L2 norm과 np_sum 함수 활용해서 error 정의
    error = ((_y - y_batch)**2).mean()

    # Error graph 출력하기 위한 부분
    errors.append(error)

print("w : {} / b : {} / error : {}".format(w, b, error))

3. w랑 b의 미분은 왜 구하는건데?

가중치(w)와 편향(b)의 편미분은 왜 구하는거고? 이걸로 뭘 할 수 있는데?

역전파 (backpropagation) 기본 개념 을 통해 알 수 있다!

3.1 역전파 기본 개념

가중치(w)와 편향(b)의 값들을 조정하여 cost function이 최소가 되도록 하는 gradient-descent 개념을 이해했다면 어떻게 이 값들을 조절해야 할까? 라는 의문이 생긴다.

그래서 w,b를 편미분 하는 이유는

가중치(w)나 편향(b) 값을 아주 작게 변화를 시키면, 즉 편미분을 시키면,
출력 쪽에서 생기는 변화 역시 매우 작은 변화가 생기며, 작은 구간만을 보았을 때는 선형적인 관계가 있다

때문이라고 한다.

즉, 작은 변화의 관점에서는 선형적인 관계이기 때문에, 출력에서 생긴 오차를 반대로 입력 쪽으로 전파시키면서 w와 b등을 갱신하면 되는데 이때 w와 b는 무작위로 변화시키는 것이 아니라, cost function이 w와 b의 함수로 이루어 졌기 때문에, 출력 부분부터 시작해서 입력 쪽으로 순차적으로 cost function에 대한 편미분을 구하고 얻은 편미분 값을 이용해 w와 b의 값을 갱신시킨다!

참고

모든 코드는 부스트캠프 AI Tech교육 자료 참고