Causal Inference | AB Test

인과관계를 설명하기 위한 방법은
1) Potential Outcomes 2) Causal Graphical Models 가 존재함

1. Potential Outcomes

1. Ideal

• A라는 사람이 존재
• Fact : 실제 과거에 X를 선택하여 얻은 현재의 결과 Y
• Assumption : 과거에 X^를 선택했으면 얻을 수 있을 결과 Y^
• Fact vs Assumption의 결과 차이를 이끌어 낸 것은 단 하나, 선택지 X vs X^ 중 무엇을 골랐는가
• 즉 Y와 Y^의 차이는 선택지 차이로 인한 인과적 영향
• BUT 실제 현실 세계에서 위의 방법을 사용할 순 없음

2. Reality

• Fact의 데이터는 보유하고 있으니
• Assumption의 데이터는 예측해서 채워넣어야 함

How?

1. 데이터 추출 Target

   1) Matching > A와 유사한 조건을 가진 사람들

   • A와 유사한 조건을 가진 사람들이 X^를 선택했을 때 얻는 결과 Y^를 추정해서 평균낸 값으로 넣자
   • Average Treatment Effect(ATE)
   • 위의 대상에 대하여 반복하여 평균적인 효과를 구함

   2) Stratification > A와 유사한 조건을 가진 사람들끼리 그룹을 구성

   • 변수가 많아지면 스코어값을 구하여 비슷한 점수의 사람들로 구분하기도 함
   • 그룹별로 평균 Y^값을 구해서 ATE를 추정

3. 정리

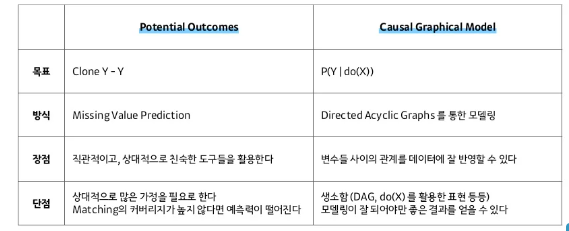
• Potential Outcomes는 인과 문제를 결측치 예측 문제로 변경하여 추정
• 그러나 이 방법은 변수들 간의 관계를 고려하지 않았음
• 즉, 인과관계가 아닌 상관관계만을 생각한 것
• Potential Outcomes는 Confounder 즉, 교란변수의 효과를 무시한 것

[참고] 변수간 상관관계 해석시 주의사항

전통적인 통계 방식으로 Causal 관계를 확인하는 것은 아래와 같은 3가지 이유로 쉽지 않음

1. Spurious Correlation 허위 상관

• 둘 이상의 변수가 통계적으로 상관되어 있지만 인과관계가 없는 관계
• 상관관계가 존재한다는 것이 인과관계가 존재한다는 의미는 아니다
• Example > 사람이 가장 많이 죽은 Year에 사과가 풍년이다 > 데이터는 상관관계가 있더라도(비례/반비례의 관계가 존재한다 가정) 인과관계가 존재하지는 않음

2. Simpson's Paradox

• 동일한 데이터도 어떻게 보느냐에 따라 다른 결과를 도출할 수 있다는 역설
• 전체 데이터를 하위 그룹으로 나누었을 때, 각 하위 그룹에서는 전체 데이터의 결과와 정반대의 결론이 나오는 현상
• Example
  - 전체 인구 기준으로 봤을 때, 약을 먹은 사람은 (질병으로)죽을 가능성이 높다는 결과가 나옴
  • (하위집단)남자와 여자를 나눠서 봤을 때, 약을 먹은 사람은 살 가능성이 높다는 결과가 나옴

Reasons for the Outcomes

• Confounder(교란변수)가 존재하기 때문에
• 성별이 약과 질병에 영향을 미치고 있었기 때문
• 즉, 성별은 약과 질병 2개 모두에 영향을 끼치는 Confounder
  - 여성의 30%만 약을 먹었고, 남성의 50%가 약을 먹음
  - 여성의 DNA가 해당 질병에 취약함
  
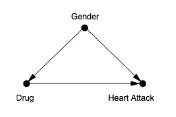
• 즉, 위의 데이터를 대상으로는 하위집단으로 나눠서 데이터를 분석해야 함
• BUT, 언제나 이렇게 봐야 하는 것은 아님 > Confounder가 존재하는지 아닌지를 확인하고 전체 데이터 분석 vs 하위집단 데이터 분석을 결정해야 함
• 아래의 이미지에서 혈압 변수는 Confounder가 아님
  

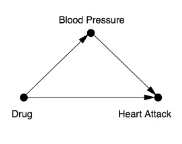
3. Berkson's Paradox

• 변수간 상관관계를 잘못해석할 경우가 존재함
• Example
  - A를 대상으로 변수 B와 C의 연관성을 분석함
  - A를 대상으로 했을 때는 변수 B와 C의 Odds Ratio가 높게 나와, 높은 연관성을 보여줌
  • 그러나 General한 사람들을 대상으로 변수 B와 C의 Odds Ratio는 낮은 값을 얻어, 낮은 연관성을 보여줌
• 위의 결과는 변수 B와 C가 변수 A에 원인이 되는 변수이기 때문에 나타난 오류 > A는 Collider 충돌변수
• 따라서 변수간 관계에 왜곡이 일어난 것

Therefore, 데이터 생성 과정부터 고민하고, 이를 통해 인과관계를 추론해야 함

2. Causal Graphical Models

1. Directed Acyclic Graphs(DAG)

• DAG로 인과관계 표현하기
• 변수간의 관계를 Graph로 나타내면 인과 관계를 명확하게 이해할 수 있음
• Potential Outcomes 모형에 필요한 조건부 독립 가정들을 Graph를 통해 검증 가능함

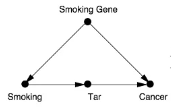
1. Chain : 각 변수가 다른 변수 하나에 funnel적으로 영향을 미치는 형태

2. Fork : 하나의 변수가 2개의 변수에 영향을 미치는 형태

3. Collider : 2개의 변수가 하나의 변수에 영향을 미치는 형태

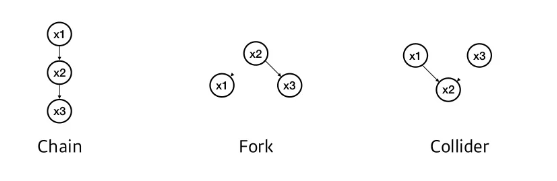
• 원인과 결과 (X > Y)
• 우리가 알 수 있는 것은 P(Y|X) : X를 선택했을 때 결과 Y
• 확인하고 싶은 것은 P(Y|do(X)) : X^를 선택했을 때 결과 Y^
• P(Y|do(X))를 어떻게 확인할까
  - 특정 형태의 그래프가 그려지면, 관찰한 데이터를 통해 변화의 영향을 측정할 수 있음
  1) Simple case 2) Back-door Adjustment 3) Front-door Adjustment

SCM(Structural Causal Models)으로도 확인할 수 있음. 수학적 equation으로 바꾼 식.

2. P(Y|do(X)) 추정 방법

변수간 구조를 알면 어떤 변수를 보정해야 하는지 알 수 있음
P(Y|X)로 P(Y|do(X))를 알 수 있음

1. Simple Case

• X > Y
• P(Y|X) = P(Y|do(X)) 인 경우

2. Back-door Adjustment

• Z가 X와 Y에 동시에 영향을 미치고 있을 경우
• X, Y, Z 모두 측정 가능해야 함
  

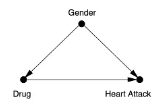
3. Front-door Adjustment

• 측정 불가능한 Confounder Z가 X와 Y에 영향을 미치고 있을 경우
• Z는 측정 불가능하지만 X, Y, a는 측정 가능해야 함
  

추가 확인 사항

1. (((causal inference 인과 추론이 있고 causal discovery가 있음. discovery는 거의 불가능한 것이 아닌가 라는 생각이 있는데(결과 데이터 보고 어떤 causal structure가 존재하는지 확인하는것) 뭐 그런 발전이 있긴 한가봄

Causal Inference
인과 추론의 출발점은 인과 모델입니다. 즉, 최소한 어떤 변수가 서로를 수신하는지 알아야 합니다. 예를 들어, X가 Y를 유발한다는 것은 알 수 있지만 상호 작용의 세부 사항은 알 수 없습니다.

There are many facets to causal inference such as estimating causal effects, using do-calculus, and breaking down confounding. I will introduce and explore these topics in the next post of this series on causal inference.

Causal Discovery
In causal inference, the causal structure of the problem is often assumed. In other words, a DAG representing the situation is assumed. In practice, however, the causal connections of a system are often unknown. Causal discovery aims to uncover causal structure from observational data.

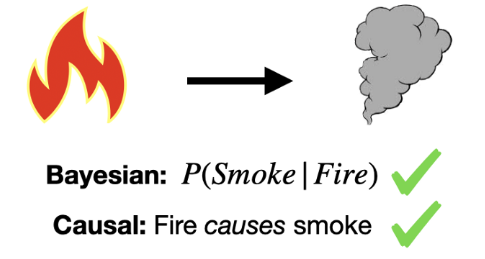
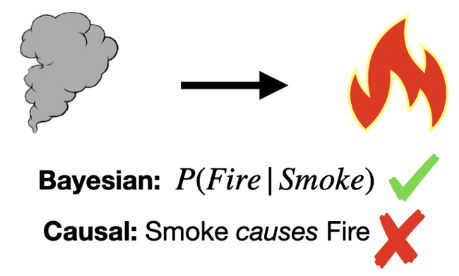
2. Bayesian vs Causal Networks

• Bayesian : 노드를 변수로 보고 arrow를 conditional probability로 봄
• Causal Network : 노드를 변수로 보고 arrow는 causal connection으로 봄
• 앞 뒤를 reverse하면 말이 되고, 안되고가 차이가 있음

3. Causal Inference 가 좋은 이유
   Gift 1: The do-operator
   X에 대한 개입이 Y의 변화를 초래하는 경우 X가 Y를 유발하는 반면 Y에 대한 개입이 반드시 X의 변화를 초래하는 것은 아닙니다

• 특히 do-calculus는 중재 분포(do-operator가 있는 확률)를 관찰 분포(do-operator가 없는 확률)로 변환할 수 있습니다. 이는 아래 그림의 규칙 2와 3에서 확인할 수 있습니다.
  

Gift 2: Deconfounding Confounding

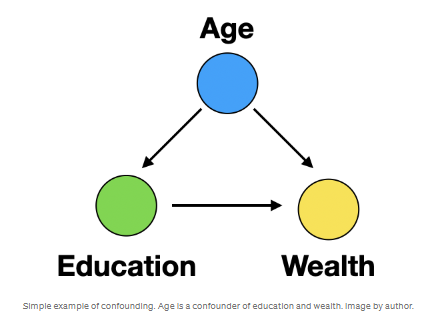
이 예에서 나이는 교육과 부의 혼동 요인입니다. 다시 말해, 교육이 부에 미치는 영향을 평가하려면 연령에 맞게 조정해야 합니다. 연령을 조정(또는 조건화)한다는 것은 연령, 교육 및 자산 데이터를 볼 때 연령 그룹이 아닌 연령 그룹 내의 데이터 포인트를 비교한다는 것을 의미합니다.

연령이 조정되지 않으면 교육이 부의 진정한 원인인지 아니면 부의 상관 관계인지 명확하지 않을 것입니다. 다시 말해, 교육이 부에 직접적인 영향을 미치는지 아니면 공통된 원인이 있는지 알 수 없습니다.

간단한 예의 경우 DAG를 볼 때 교란은 매우 간단합니다. 3개의 변수에 대해 교란자는 2개의 다른 변수를 가리키는 변수입니다. 그러나 더 복잡한 문제는 어떻습니까?

여기서 do-operator는 명확성을 제공합니다. Pearl은 do-operator를 사용하여 혼란을 명확하게 정의합니다. 그는 혼란이란 P(Y|X)가 P(Y|do(X))[1]와 다르게 되는 모든 것이라고 말합니다.
confounding is anything that leads to P(Y|X) being different than P(Y|do(X)) [1].

Gift 3: Estimating Causal Effects

Dowhy Flow

1. Define causal model with DAG

# Define causal model
model=CausalModel(data = df,         
                  treatment= "hasGraduateDegree",         
                  outcome= "greaterThan50k",         
                  common_causes="age",         
                  )
# View model
model.view_model() 
from IPython.display import Image, display display(Image(filename="causal_model.png"))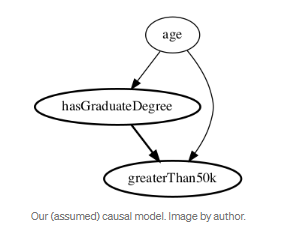

2. Estimand

• 목표하는 인과관계를 제공하는 방법
• 교육이 소득에 미치는 영향을 계산하는 방법을 알려줌
  

3. compute the causal effect

• target에 대한 ATC를 추정하는 EconML 라이브러리의 meta-learning 을 사용

# Compute causal effect using metalearner
identified_estimand_experiment = model.identify_effect(proceed_when_unidentifiable=True)

from sklearn.ensemble import RandomForestRegressor
metalearner_estimate = model.estimate_effect(identified_estimand_experiment,                             method_name="backdoor.econml.metalearners.TLearner",
confidence_intervals=False,
method_params={
     "init_params":{'models': RandomForestRegressor()},
     "fit_params":{}
              })
print(metalearner_estimate)
`![](https://velog.velcdn.com/images/js8456/post/10ce6694-6490-4f92-9008-4248adfb9a0a/image.png)

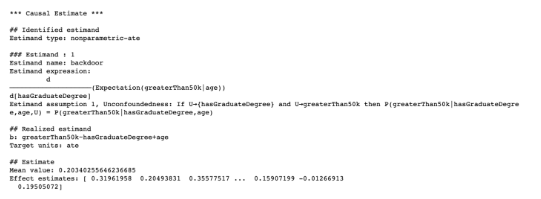
평균 인과 효과는 약 0.20입니다. 이는 대학원 학위를 취득하면 연간 $50,000 이상을 벌 확률이 20% 증가한다는 의미로 해석될 수 있습니다. 이것이 평균 효과라는 점에 유의하여 평균이 대표성인지 여부를 평가하기 위해 값의 전체 분포를 고려하는 것이 중요합니다.

위의 그림에서 우리는 표본에 걸친 인과적 영향의 분포를 볼 수 있습니다. 분명히 분포는 가우스 분포가 아닙니다. 이는 평균이 전체 분포를 대표하지 않는다는 것을 알려줍니다. 인과 관계를 기반으로 한 집단에 대한 추가 분석은 '누가'가 대학원 학위에서 가장 많은 혜택을 받는지에 대한 실행 가능한 정보를 찾는 데 도움이 될 수 있습니다.

모든 인과 추론의 출발점은 인과 모델입니다. 그러나 일반적으로 우리는 좋은 인과 모델을 가지고 있지 않습니다. 여기에서 인과관계 발견이 도움이 될 수 있으며, 이는 다음 포스트의 주제입니다.

참고페이지
https://towardsdatascience.com/causal-inference-962ae97cefda

추가 내용 _ timeseries

Dowhy가 만드는 주요 가정은 데이터의 모든 행이 iid로 샘플링된다는 것
근데 timeseries data는 이 가정을 위반하지, 모든 연속되는 행들이 종속되어있기 때문에. 이를 해결하려면 시간 t의 데이터가 이전 값에 어떻게 의존하는지에 대한 가정이 필요함

timeseries데이터분석예시

Causal Discovery

Causal discovery aims to infer causal structure from data. In other words, given a dataset, derive a causal model that describes it.

인과 관계 발견은 역 문제의 예입니다. 이는 마치 조리대에 남겨진 물웅덩이를 보고 각얼음의 모양을 예측하는 것과 같다

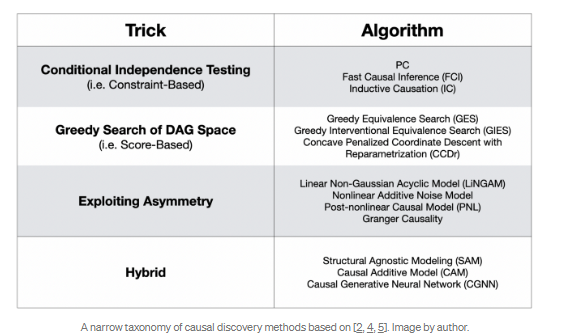
Causal Discovery Toolbox Official Document

잠깐 정리하자면 1) Causal Discovery > Dowhy DGA Modeling 하고 결과 본다 2) 내가 Modeling 해서 > Dowhy 결과 본다 3) 다른 국가와 비교하여 결과 창출한다

Causal Impact & Causal Forest

causal forest는 각 고객군별 causal impact 확인 라이브러리
https://tv.naver.com/v/23650648

Causal Inference를 진행하는 이유

통계적 추론 및 기계 학습 모델은 데이터에서 상관 관계를 찾는 데 탁월하지만 결과의 실제 원인을 항상 찾지 못할 수도 있습니다. SHAP와 같은 기능 중요도 방법의 사용과 데이터 세트에서 가장 중요한 기능을 얼마나 잘 식별할 수 있는지 생각해 보십시오. 의사 결정의 관점에서 중요도 점수가 가장 높은 기능이 항상 행동하기에 가장 좋은 것은 아니며 결과에 전혀 영향을 미치지 않을 수도 있습니다. 인과적 추론은 그 이유를 이해하는 데 도움이 됩니다.

Causal Inference의 어려움
참고사이트
1. 실제로 일어난 결과만을 확인할 수 있음 : factual
2. T0 시점에서 Intervention/Treatment가 발생함으로 Y(결과)에 영향을 미침 > Causal Effect는 T의 변화량에 따른 Y의 변화
3. Y에 영향을 미치는 다른 것들은 확인이 불가함 : Counterfactual
따라서 1) 반대 사실의 효과를 직접 계산할 수 없고 2) 추정에 의존해야 하며 3) 검증을 수행할 때 몇 가지 문제를 예상해야 합니다.

Dowhy

Methodology
Judea Pearl sets forth a four steps process in his seminal work, based on the Structural Causal Model (SCM):

Define: Express the target quantity Q as a function Q(M) that can be computed from any model M.
Assume: Formulate causal assumptions using ordinary scientific language and represent their structural part in graphical form.
Identify: Determine if the target quantity is identifiable (i.e., expressible in terms of estimable parameters).
Estimate: Estimate the target quantity if it is identifiable, or approximate it, if it is not. Test the statistical implications of the model, if any, and modify the model when failure occurs.

4 Step
Modeling: Create a causal graph to encode assumptions.
Identification: Formulate what to estimate.
Estimation: Compute the estimate.
Refutation: Validate the assumptions.

통제 집단 필수 유무

1. DID
   Look-forward-Matching으로 통제 집단 설정
   X 기간 Intervention 100% 배포 => 통제 집단
   vs Y 기간

2. CausalImpact
   대조군으로 유추할 수 있는 데이터 없음
   Intervention 이전의 데이터를 기반으로, Intervention 이후 기간의 데이터를 예측함 > synthetic control > 가상의 대조군
   실제데이터와 Difference를 확인함으로 인과 효과를 추정함
   

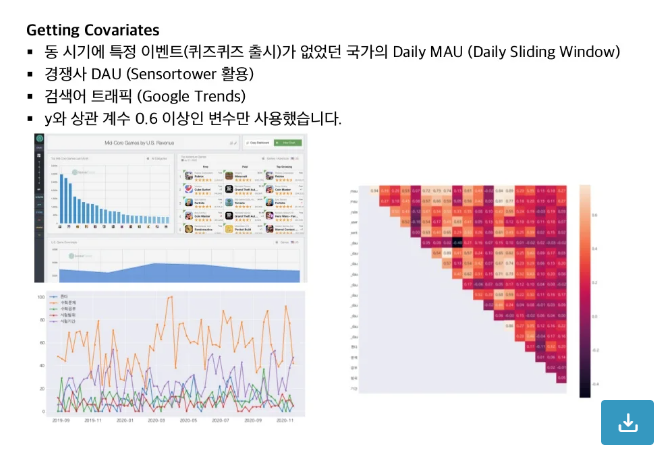
CausalImpact의 경우 개입에 의해 영향을 받지 않는 설정된 제어 시계열이 있다고 가정합니다. 그렇다면 실제 효과를 잘못 과소 평가하거나 과대 평가할 수 있습니다. 또는 실제로는 효과가 없는데도 효과가 있다고 잘못 결론을 내릴 수도 있습니다. 이 모델은 또한 사전 기간 동안 설정된 공변량과 처리된 시계열 간의 관계가 사후 기간 동안 안정적으로 유지된다고 가정합니다(이 가정을 완화하는 방법은 model.args$dynamic.regression 참조). 마지막으로, 모델의 일부인 사전을 아는 것이 중요합니다(특히 model.args$prior.level.sd 참조).

주요 가정

Y에서 일어나는 변화는 Synthetic control 값을 예측할 때 들어가는 변수들에 영향을 주지 않는다.
Y와 변수의 관계는 개입(intervention)이 없었다면 계속되었을 것이다.
제안하는 데이터의 조건 (Rule of thumb)

이벤트 이후 기간이 1 ~ 3주 정도의 길이일 때 가장 이상적이다.
이벤트 이전 기간이 이벤트 이후 기간의 3–4배 가까이 길어야 좋다.
주요한 구조적인 변화가 전체 기간 통틀어서 없을 것.
“Garbage in, garbage out” 을 강조한다. Causal Impact 모델이 예측한 효과가 더 타당성을 가질 수 있도록 튜닝하는 과정은 대부분 counterfactual 데이터를 예측하는 변수를 찾고 검증하는 과정이다. 이 변수 는 주로 사람의 판단으로 구성되는데, 2. Ladder of Causality 에서 이야기했듯이 변수와 예측치의 인과 관계를 고민해본 후 변수를 추가해주는 것이 중요하다.
https://medium.com/bondata/quasi-experiments-%EC%9D%B8%EA%B3%BC-%EA%B4%80%EA%B3%84-%EC%9D%B4%EB%B2%A4%ED%8A%B8%EC%9D%98-%ED%9A%A8%EA%B3%BC-%EB%A5%BC-%EC%B8%A1%EC%A0%95%ED%95%98%EB%8A%94-%EB%B0%A9%EB%B2%95-da34ceefc34f

Counterfactual 데이터 예측

CausalImpact

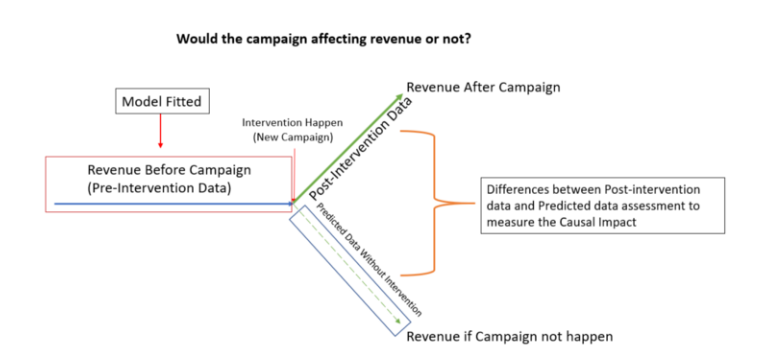
The best model is used in the “post-intervention” data (after the campaign) to forecast what would happen if the intervention never happen.

• dowhy가 timeseires에서 사용하기에 약간은 애매한데, 이 부분이 causalimpact를 사용하게끔 하는 듯

Causal Impact approached the problem is by using the Bayesian Structural Time Series to fit a model that best explains the “pre-intervention” data
The best model is used in the “post-intervention” data (after the campaign) to forecast what would happen if the intervention never happen.

영향받는 변수(response variable) 즉, intended target은 time intervention에 영향받지 않는 covariate X인 다른 변수들과 함게 linear regression으로 예측.
예를 들어 캠페인의 영향으로 인한 revenue를 찾고자 할 때, daily visit은 캠페인에 영향을 받을 가능성이 높으니 covariate로 사용하면 안됨

Using the Causal Impact, your intended target to assess should be renamed as y, and the other columns would be treated as the covariate feature.