Google Research

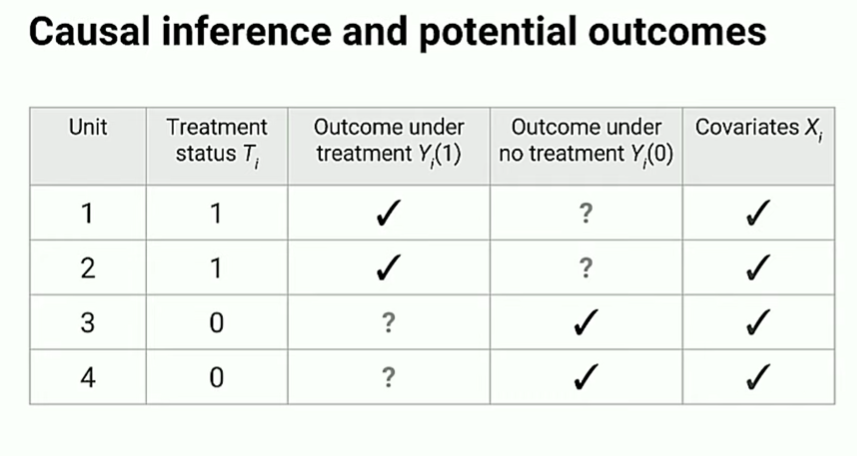
Casual Impact

• Bayesian structural model에 기반되어있고, 과거 데이터를 기반으로 미래 데이터를 예측하는 Model
• Intervention 이전의 모든 데이터를 포함하며, 실제 데이터와 Intervention이 없었을 때의 데이터를 비교함
• 즉, 실제로 관측된 결과와 개입이 없었을 때를 가정했을 때의 예측값의 차이를 그 ‘개입의 효과(causal impact)로 보는 것
• Required Data : observed data y, covariate x, intervention 이전 기간인 pre-period, intervention에 영향 받은 기간인 post-period

1. Assumption

• 통제 변수(Control) 시계열 데이터(Intervention없는)는 개입의 영향을 받지 않아야함
• Intervention 이전 공변량과 결과 변수의 관계가 개입 이후에도 유지되어야함 (dynamic regression을 적용할 경우, 이 가정을 완화시킬 수 있음)
• 모형에 Prior가 포함되어 있다는 사실을 명심해야 함 >
  CausalImpact가 시계열 학습에 사용하는 모형은 Local Level 을 위해 Gaussian random walk 를 사용하는데, 이 때 random walk의 표준 편차에 Prior가 설정되어 있기 때문(Random walk이기에 각 방향으로 무작위의 걸음 크기로 걸어다니지만 정규분포를 사용하여 걸음의 크기를 조정)

Bayesian Structural Time Series Model

1. 빈도주의 접근법을 이용하는 ARIMA와는 다름
2. Trend, Seasonality를 포함한 서로 다른 시계열 데이터간의 상관관계를 반영하는 회귀 구성 요소까지 조합한 모델
   • Trend, Seasonality를 포함하여 기타 Covariate 또한 생각한다는 것
   • 이 Covariate은 효과를 확인하고자 하는 Intervention 요소와는 관련이 없어야 함
   • Intervention이 없는 상황에서의 결과 데이터와 있는 상황에서의 데이터의 차이를 확인하고자 하는 것이기 때문에
   • 따라서, Covariate 확인 잘 해야 함
3. 칼만필터모델 or 동적선형모델 로 불리기도 함

check needed
데이터 평활에 사용되는 ?Kalman Filter(칼만 필터 방법) : 변동성 및 측정 오차의 조합으로 시계열 과정을 모델링하여 데이터를 평활함. 칼만필터와 뢰스는 시간의 전후데이터를 모두 고려하여 과거로 정보가 유출될 수 있음" 과는 다른 내용인가?

Beyesian 베이지안 VS Frequentism 빈도론
1. 빈도론

• 경험적 사실만을 중시하기 때문에 확률의 정의를 아래와 같이 내림
• 사건이 일어나는 장기적인 확률

2. 베이지안

• 알고 있는 사전 지식을 활용해서 우리가 알고 싶은 확률을 추정
• 지식이나 판단의 정도를 나타내는 수단

ex. 주사위를 던져 1이 나올 확률은 1/6

• 빈도론 : 100번 주사위를 던지면 1이 16번 나온다
• 베이지안 : 100번 주사위를 던졌을 때 1이 나온다고 16.6% 확신한다

현실적으로 모든 사건을 경험에 입각하여 결론을 예측할 수 없다는 한계를 가지기 때문에, Bayesian Decision Rule을 사용하여 확률을 추론

Covariate 공변량
분석의 주요 목적은 독립변수들이 종속변수에 얼마나 많은 영향을 끼치는가
그러나 잡음 인자가 존재하면 그 영향을 정확히 파악하기 힘듦
이 부분을 제거하기 위한 방법이 Covariate. Covariate란 종속변수에 대하여 독립변수와 기타 잡음인자들이 공유하는 변량을 의미
즉, 종속변수에 독립변수 이외의 기타 잡음인자들이 영향을 줄 수 없도록 통제하고자 하는 변수가 Covariate

Example
특정 마케팅 캠페인이 '수익'에 미칠 영향을 추론하려는 경우 총 방문수가 캠페인의 영향을 받을 수 있으므로 일일 '방문수'를 공변량으로 사용할 수 없음

Method : ANCOVA(ANOVA + Regression)

2. Installation

1. pycausalimpact

기본은 R 패키지인데 Python을 사용할 예정이기 때문에 아래의 Package를 기재

R 패키지와 Python 패키지의 차이점

• Python : 상태공간 방정식을 해결하기 위한 방법으로 classical Kalman Filter을 사용하는 statsmodels에 의존
• R : stochastic Kalman Filter technique을 사용하는 Bayesian approach (from bsts package)을 이용
• 둘이 유사하긴 하나, R에서는 사용자 사전 지식에 의존하는 접근 방식을 찾는 반면 Python은 우도 함수를 최대화하는 것을 목표로 하는 고전적인 통계 기술을 사용합니다. 구조적 시계열 구성 요소로 표현됩니다.

pip install pycausalimpact

2. tfcausalimpact _ python 3.10 미만에서 가능함

pip install tfcausalimpact 

3. Library 사용

1. pycausalimpact

• 날짜 변수가 인덱스로 설정되고 확인하고자하는 데이터가 DataFrame의 첫 번째 열에 존재해야 함

import numpy as np
import pandas as pd
from statsmodels.tsa.arima_process import ArmaProcess
from causalimpact import CausalImpact

np.random.seed(12345)
ar = np.r_[1, 0.9]
ma = np.array([1])
arma_process = ArmaProcess(ar, ma)
X = 100 + arma_process.generate_sample(nsample=100)
y = 1.2 * X + np.random.normal(size=100)
y[70:] += 5

data = pd.DataFrame({'y': y, 'X': X}, columns=['y', 'X'])
pre_period = [0, 69]
post_period = [70, 99]


# 맨 처음에 실행할 때는 statsmodel 자체적으로 
# local level component를 최적화할 수 있도록 prior_level_sd = None으로 설정
# local level prior에 확신이 있으면 설정해도 좋으나, risky할 수 있음 
# ci = CausalImpact(data, pre_period, post_period, prior_level_sd=None)


ci = CausalImpact(data, pre_period, post_period)
print(ci.summary())
print(ci.summary(output='report'))
ci.plot()

Parameter

1. prior_level_sd
   pycausalimpact documentation strongly recommends setting the prior_level_sd as None when using the Python version of the package.
   (prior_level_sd is the prior local level Gaussian standard deviation.)

2. nseasons
   nseasons specifies the seasonal components of the model.

The default value is 1, meaning that there is no seasonality in the time series data.
Changing the value to a positive integer greater than 1 automatically includes the seasonal component. For example, nseasons=7 means that there is weekly seasonality.
Currently the CausalImpact package only supports one seasonal component, but we can include multiple seasonal components using the Bayesian Structural Time Series (BSTS) model, and pass the fitted model in as bsts.model.

3. seasonal_duration
   seasonal_duration specifies the number of data points in each season.

The default value for seasonal_duration is 1. For example, nseasons=[{'period': 7}], seasonal_duration=1 means that the time series data has weekly seasonality and each data point represents one day.
If we would like to include the monthly seasonality, nseasons needs to be set to 12 and seasonal_duration needs to be set to 30, indicating that every 30 days represent one month.
In this example, we will use nseasons=[{'period': 12}], seasonal_duration=30 for the hyperparameters.

4. dynamic_regression
   동적 시계열 모형= ARIMAX 모형(Arima + 회귀모형)
   dynamic_regression is a boolean value indicating whether to include time-varying regression coefficients.

Since including a time-varying local trend or a time-varying local level often leads to over-specification, this hyperparameter defaults to FALSE.

We can manually change the value to TRUE if the data has local trends for certain time periods.

2. tfcausalimpact

import pandas as pd
from causalimpact import CausalImpact


data = pd.read_csv('*.csv', index_col=['DATE'])
pre_period = ['2019-04-16', '2019-07-14']
post_period = ['2019-7-15', '2019-08-01']

# Monte Carlo 알고리즘 사용
ci = CausalImpact(data, pre_period, post_period, model_args={'fit_method': 'hmc'}) 

csv 데이터 예시

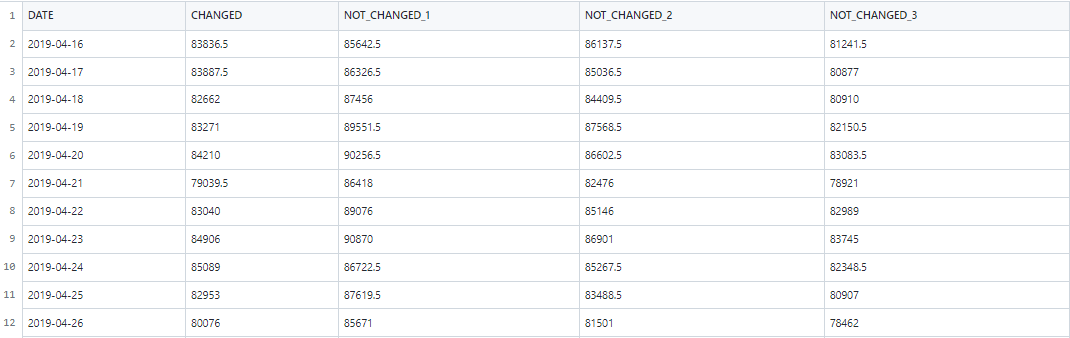
분석 예시_1_Basic 데이터
분석 예시_2 Kaggle
분석 예시_3 > Google Search Console 연결

4. 결과 해석

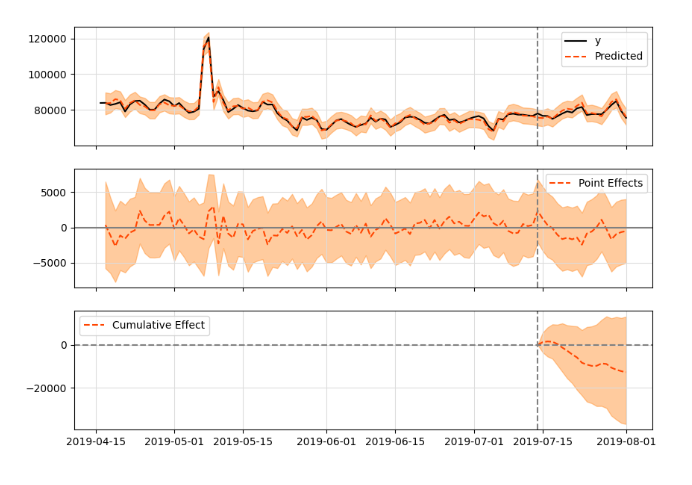
1st 이미지

• 실제값(실선)과 예측값(점선) 확인

2nd 이미지

• Causal Impact를 시계열로 표현한 이미지
• 즉, 실제값에서 예측값을 뺀 값

3rd 이미지

• Causal Impact 값을 시간 흐름에 따라 누적해서 더한 결과

• Causal Impact 부분의 신뢰구간(95%)을 봤을 때 해당 구간이 0을 포함하고 있고
• p-value가 0.29 > 즉, 실제값과 예측값 사이에 차이가 없다는 H0 귀무가설을 반박할 증거가 71%라는 의미 > usual 95%보다 낮기 때문에 귀무가설 반박이 불가함 > 즉, Intervention의 효과를 입증하기는 힘들다는 결과로 귀결됨

5. 주의 사항

1. Covariate 선정
   • stable한 covariate를 선정하기 위해 지표에 영향을 주지 않는 period를 잘 설정한 후, 그 기간 내 지표와 covariate의 변화가 비례한지 확인해야 함
   • 왜 모형에 포함된 공변량들이 개입의 영향을 받지 않았는지 고민해야 함
   • 공변량을 그래프로 그려서 시각적으로 확인해 볼 필요 존재

참고페이지1: Causal Impact Github
참고페이지2: Causal Impact - 좀 더 정확한 효과 측정을 위한 방법론

2. Intervention 이전 시계열 예측 확인 필요
   개입 이전 시점까지의 시계열을 얼마나 잘 예측하는지 확인해야 합니다. 임의의 시점에 가상의 개입이 이루어졌다고 가정하고 모형을 학습하면 어떤 결론이 나오는지 확인해봅니다. 이 때 counterfactual 예측과 실제값이 비슷해서 통계적으로 유의미하지 않은 결론이 나와야 합니다.

3. 모형의 학습 결과를 공유할 때는 가정한 내용들과 모형의 파라미터를 포함하여 공유합니다. 다른 사람들과 함께 유효한 가정인지, 적절한 파라미터를 사용한 것인지 논의하는 것이 좋습니다.

6. Shop에서 확인할 수 있는 Variables

1. Revenue

   • Total Revenue
   • Total Order Volume

2. Conversion

   • Buy Page > Cart Page
   • Cart Page > Checkout Page
   • Checkout Page > (Payment Options) > Order

3. LTV(Lifetime Value)

   • Trade-In과 같은 Service를 이용한 Customer 대상 LTV 얼마나 상승했는지 확인 가능