우리는 지금부터 가우스 소거법 (Gaussian Elimination)과 LU 분해 (LU Decomposition)에 대해서 공부해볼 것이다.

우선은 여러분이

1. 벡터와 행렬의 기본적인 성질들에 대해서 알고,
2. Ax = b를 푸는 경우 중에서도,
   n개의 미지수와 n개의 방정식을 지녔으며,
   해가 단 하나뿐인 아주 특수한 케이스를 푼다는 것을 안다고 생각하고 진행하도록 하겠다!

Gaussian Elimination

우리가 고등학교 때 연립방정식을 풀 때, 어떻게 했었는가?
보통은 계수를 맞춰서 문자를 소거하거나, 정리된 식을 다른 식에 대입하는 방식으로 문제를 풀었었다.

문제에 맞게, 성향에 맞게 알아서 풀라고 배웠었지만...
컴퓨터에게 그렇게 하라고 할 수는 없으니,
획일화된 풀이 방법을 가르쳐 줘야겠고, 그것이 가우스 소거법이다!

출처 : https://pbs.twimg.com/media/EFX1KQlU0AETKmv.jpg

Pivot을 이용한 Triangular system 만들기

Triangular는 대충 삼각형이겠고,,, Pivot은 뭘까?

3개의 미지수와 3개의 방정식이 담긴 예시로 알아보자!!

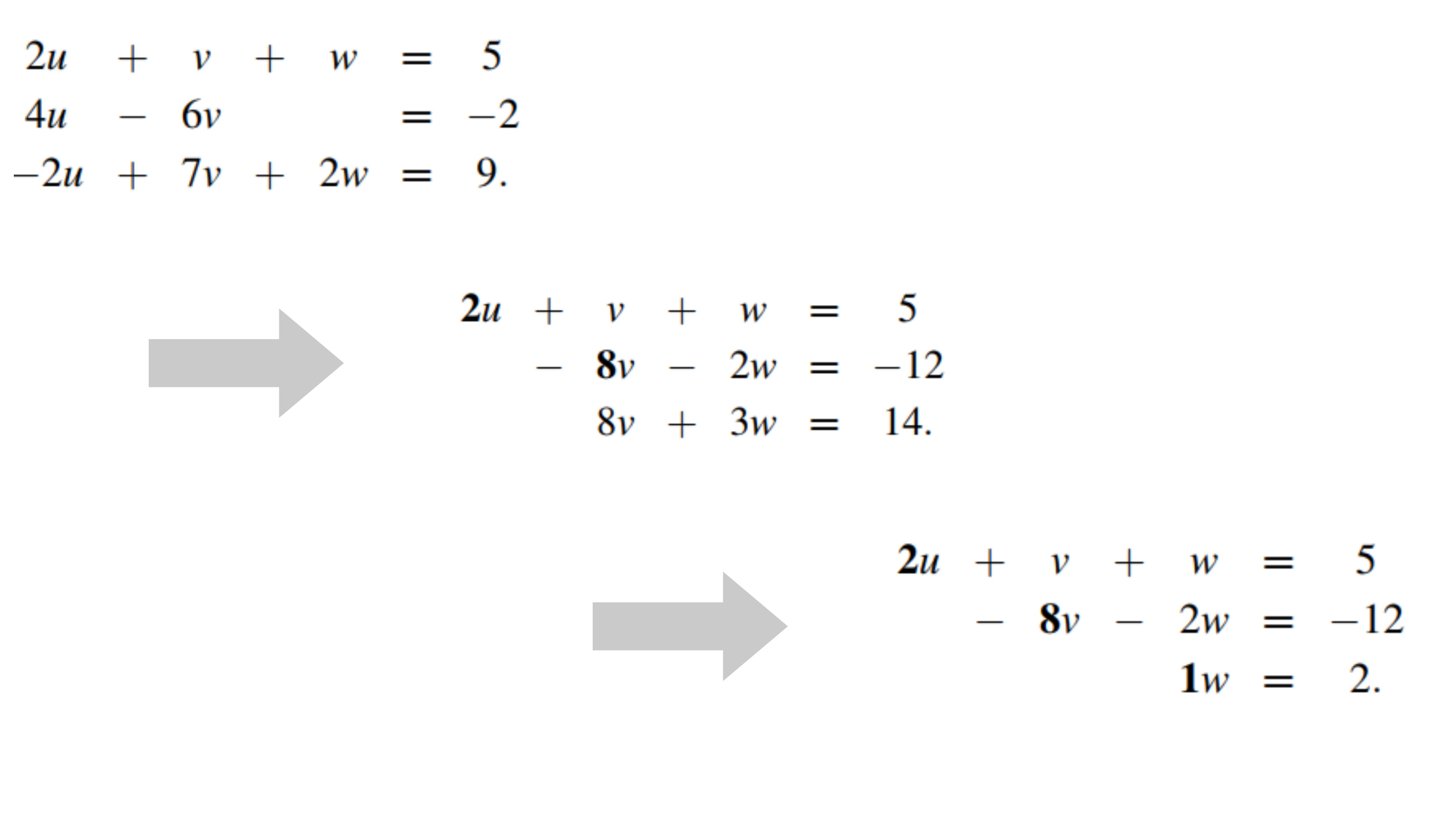출처 : [선형대수와 그 응용]

위에서 말했다시피, 보통은 계수를 맞춰서 문자를 소거한다고 하였는데,
그 기준이 되는 숫자들이 바로 Pivot이다!

첫번째줄의 첫번째요소를 Pivot으로 잡고, 2,3번째 줄의 첫번째 요소를 없애고
두번째줄의 두번째요소를 Pivot으로 잡고, 3번째 줄의 두번째 요소를 없애고 나면

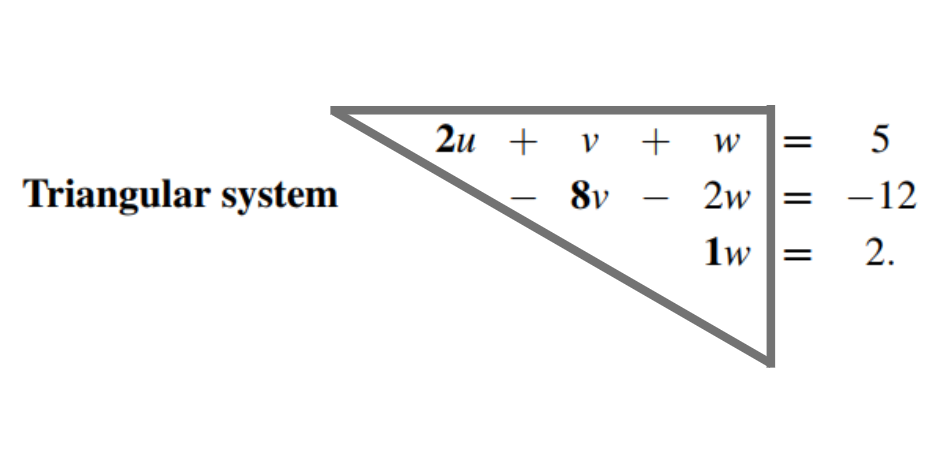
오른쪽 위의 삼각형 모양의 부분만 남게 되는데, 이것이 바로 Triangular system이다.
Upper Triangle이여서 U라고도 부른다.

Back Substitution

위의 그림에서,
마지막 줄의 w값을 두번째 식에 대입하고,
그렇게 나온 v와 w값을 첫번째 식에 대입하면,

라는 해가 나오게 되는데,
역으로 올라가면서 대입하기 때문에, Back Substitution이다.

오잉??? 그러면 끝이에요? 너무 쉬운데??

그럴리가 있나. 컴퓨터는 데이터를 어떻게 다룬다구요??

Matrix Form of Elimination Step

맞습니다 매트릭스, 행렬로 다룹니다.

Triangular System을 만드는 위의 과정을

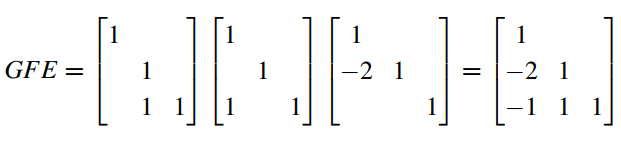
이러한 Matrix(들)을 곱해주는 것으로 표현할 수 있다.

첫번째 step인 행렬 E만 풀어서 설명하자면,

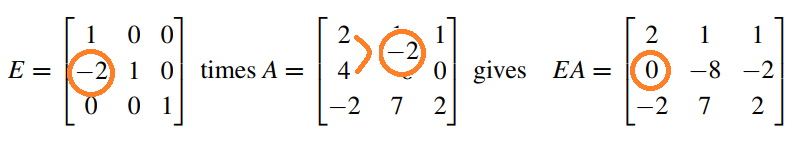
1(j)번째 pivot으로 2(i)번째 줄의 첫번째 요소를 제거하기 위한 계수인 -2가,
항등행렬의 $a_{21}, \ (a_{ij})$ 자리에 들어간 행렬이 Matrix Form of Elimination Step인 것이다.

그래서 결론이 LU분해?!

아니 그래서 어떻게 LU 분해가 되는거죠?
침착하게 이 놀라운 과정들을 살펴보시라.

위의 Triangular system을 만드는 과정을 행렬로 수식화 하면 다음과 같다.

그런데 Elimination Step인 G, F, E 이 친구들이, 정말 기가 막히게도,
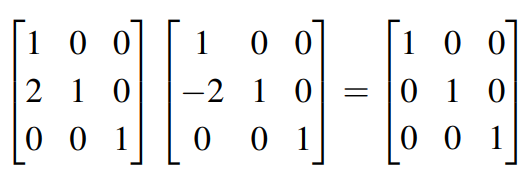역행렬이 요렇게 예쁘게 구해진다. (행렬의 ij번째 요소의 부호만 바꿔주면 역행렬!)

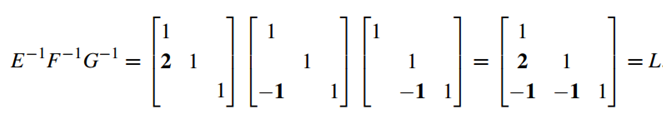
이 친구는 아까와 반대로 왼쪽 아래의 삼각형 모양이기에, Lower Triangle, L이라 부른다.

그렇다면, 행렬의 성질들에 의해서

출처 : MBC 무한도전

후우,,, 드디어 끝났다! 그럼 다음 시간에 Gauss Jordan Method로 이어가 보겠다! 20000!