이 문서는 필자가 배운 벡터의 기본적인 특성들에 대해서 기술한다.
기본적이지 않을 수도, 내용이 틀릴 수도 있으니 피드백은 언제나 환영이다!
Linearity (선형성)
'선형'대수학이니, 선형성부터 알아보자.
수식으로 표현하면,
f(ax1+bx2)=af(x1)+bf(x2)
사실 아래의 두가지의 성질이 합쳐져서 나타난 것이다.
-
Superposition (중첩)
f(x1+x2)=f(x1)+f(x2)
-
Homogeneity (동종성)
f(ax)=af(x)
Vector (벡터)
Magnitude(크기) + Direction(방향, orientation)
혹은 여러 개의 숫자(데이터)가 특정한 순서대로 모여 있는 것
아래와 같이 표기한다.
x=⎣⎢⎢⎢⎢⎡x1x2⋮xN⎦⎥⎥⎥⎥⎤
또는
x∈RN
컴퓨터가 다루는 데이터들은 숫자로 구성되어있고,
하나씩 넘겨주는 것보다 묶어서 넘겨주는 것이 나으므로, 자연스레 벡터를 쓸 수 밖에 없다!
Linear Combination (선형조합)
여러 개의 벡터를 스칼라곱을 한 후 더한 것
c1x1+c2x2+⋯+cNxN
이 식에서 c1,⋯,cN은 스칼라 계수다.
이잉? 갑자기 곱하고 더한다고? 아래의 두가지 개념을 살펴보고 다시 오면 된다.
스칼라와 벡터의 곱
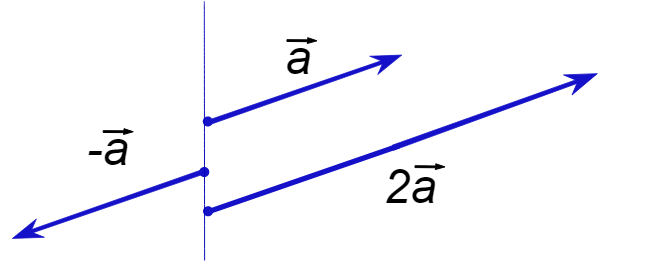
양의 실수와 벡터를 곱하면 벡터의 방향은 변하지 않고 실수의 크기만큼 벡터의 길이가 커진다.
만약 음의 실수를 곱하면 벡터의 방향이 반대가 된다.
그림으로 간단히 이해하자
 출처 : Google CCL
출처 : Google CCL
벡터의 합
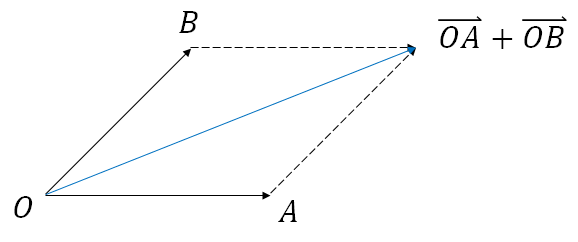
벡터와 벡터의 합도 벡터가 된다.
이때 두 벡터의 합은 그 두 벡터를 이웃하는 변으로 가지는 평행사변형의 대각선 벡터가 된다.
a=[12],b=[34]→c=a+b=[46]
그림으로 간단히 이해하자
 출처 : Google CCL
출처 : Google CCL
Magnitude, Norm (벡터의 크기, 놈)
벡터의 크기는 Norm이라는 것으로 나타낸다.
∥X∥p=(i=1∑N∣xi∣p)1/p
기본적인 형태는 위와 같으나, 보통 p=1, p=2, p=∞ 인 경우를 자주 사용하고,
- L2Norm : ∑(xi)2
- L1Norm : ∑∣xi∣
- L∞Norm : maxi∣xi−yi∣
그중에서도 p=2인 L2Norm이 주로 쓰인다.
Inner Product (내적)
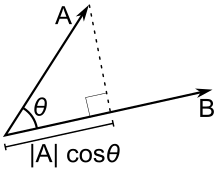
x⋅y=∣∣x∣∣⋅∣∣y∣∣⋅cosθ=∑xiyi
위의 식에서 ∣∣y∣∣⋅cosθ는, 벡터 y의 벡터 x에 대한 투영길이가 된다.
그림으로 이해해보자
 출처 : 위키피디아
출처 : 위키피디아
단위벡터 (unit vector)
길이가 1인 벡터
예를 들어 다음과 같은 벡터들은 모두 단위벡터다.
a=[10],b=[01],c=⎣⎢⎢⎡2121⎦⎥⎥⎤
다음 벡터는 벡터 자신의 크기인 L2Norm으로 나눠주었기 때문에,
벡터 x와 같은 방향을 가리키는 단위벡터가 된다.
∥x∥x
Orthogonality (직교)
두 벡터 x와 y가 이루는 각이 90도이면 서로 직교(orthogonal)라고 한다.
cos90∘=0이므로 서로 직교인 두 벡터의 내적은 0이 된다.
xTy=yTx=0↔x⊥y
Vector distance (유클리드 거리)
두 벡터가 가리키는 점 사이의 거리
두 벡터의 유클리드 거리는 벡터의 차의 길이로 구할 수 있다.
벡터의 놈의 정의를 통해 유클리드 거리는 다음처럼 구한다.
d=∥X−Y∥=i=1∑(xi−yi)2
또한, 루트 안에 있는 식은 다음과 같이 펼칠 수 있다.
∥x−y∥2=∥x∥2+∥y∥2−2xTy  출처 : Google CCL
출처 : Google CCL 출처 : Google CCL
출처 : Google CCL 출처 : 위키피디아
출처 : 위키피디아