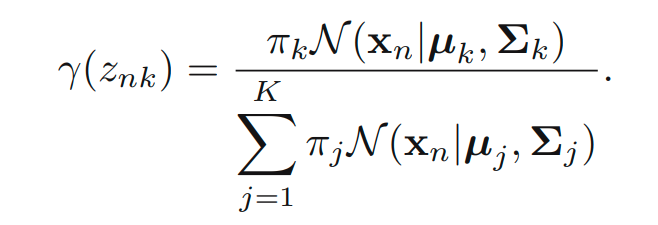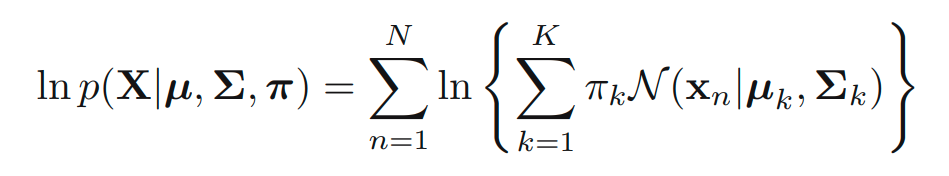시작하며,

여전히, keypoint 기반으로 object matching을 하는 연구를 진행하고 있습니다. 이번에는 방향성을 살짝 바꿔서 keypoint의 정보와 coherent point drift의 개념을 활용해보기로 했습니다. 하지만, coherent point drift가 EM 기반의 알고리즘이어서 EM을 복습해봐야겠다는 생각이 먼저 들더군요! 그래서 이번에는 EM을 리뷰해봤습니다.
위 링크의 9장 전체를 읽어서 핵심적인 내용만 간추려봤습니다. 그럼 시작해볼까요?!
9.1. K-means Clustering
우선, 다차원 공간에 있는 데이터의 그룹 혹은 클러스터를 식별해내는 문제를 고려해봅니다. D 차원을 가지는 N개의 data points를 모아둔 set {}을 생각해봅니다. 우리의 목표는 data set을 K개의 clusters로 분할(partition)하는 것 입니다. 이때, K는 주어져 있다고 가정합니다. 직관적으로 생각해봤을 때, cluster 내부의 한 data point에서 cluster 내부에 있는 data point까지의 거리가 cluster 바깥의 data point까지의 거리보다 상대적으로 작을 것으로 예상할 수 있습니다. 이를 수학적인 formulation으로 재구성해봅시다.
{}, k = 1, ..., K
를 중심으로 가지는 K개의 clusters를 위의 수식으로 생각해볼 수 있습니다. 각 data point와 가장 가까운 cluster의 중심()과의 거리의 제곱 합이 최소가 되기를 바랍니다. 이를 수학적으로 나타내기 위해 binary indicator variables {0, 1}을 정의합니다.
어떤 data point 이 cluster k에 할당 되어있다면 이고 입니다. (1-of-K coding)
위의 정의들을 활용해 objective function을 다음처럼 정의할 수 있습니다.
우리의 목표는 J를 최소화하는 {}와 {}를 찾는 것입니다. {}와 {} 각각에 대해 연속적인 최적화 문제를 해결해나가면서 문제를 해결할 수 있습니다. 아래의 두 process를 수렴할 때까지 반복적으로 수행합니다.
1) 를 고정하고 에 대해 J를 minimize합니다.
2) 를 고정하고 에 대해 J를 minimize합니다.
이 두 process는 EM에서의 E step, M step과 유사합니다. EM의 맥락에서 K-means Clustering을 알아보도록 하겠습니다.
J는 에 대해 linear 하므로 optimization을 통한 결과를 closed form으로 쉽게 얻을 수 있습니다. 이때, J의 n개의 term을 독립적으로 최적화해줍니다. data point 에 대해 가장 가까운 cluster center와 matching 시켜주는 방식으로 J를 minimize 할 수 있습니다.

다음으로 를 고정하고 에 대해 J를 최적화합니다. J는 에 대한 2차 함수이므로 미분해서 0이 되도록 하는 값이 J를 최적화시킨다는 것을 알 수 있습니다. 따라서 아래의 식을 정리해 를 구할 수 있습니다.


위 식의 분자와 분모를 살펴보면 다음을 알 수 있습니다.
1) 분자: cluster k에 할당된 data point의 총합
2) 분모: cluster k에 할당된 data point의 개수
따라서 이는 곧 cluster k로 할당된 data points의 평균임을 알 수 있습니다. 이러한 이유로 위의 절차를 K-means algorithm이라고 부르고 있습니다. K-means algorithm은 data의 assignment가 바뀌지 않을 때까지(수렴) 반복합니다. 아래의 예시를 통해 좀 더 직관적으로 K-means algorithm에 대해서 알아보도록 하겠습니다.

(a) 초록색으로 표시된 data points를 두 개의 cluster로 할당하려고 합니다. 과 의 초깃값은 각각 red cross, blue cross로 표기합니다.
(b) E step: 각 data point가 어떤 cluster로 할당되는지에 대해 판정합니다. 위에서 살펴본 optimal 를 찾는 과정이라고 볼 수 있습니다. magenta 색깔의 라인은 과 의 수직이등분선입니다. 이 라인을 기준으로 data point를 쉽게 나눌 수 있습니다.
(c) M step: 분류된 data point를 기준으로 새로운 과 를 계산합니다.
(d) E step
(e) M step
(f) E step
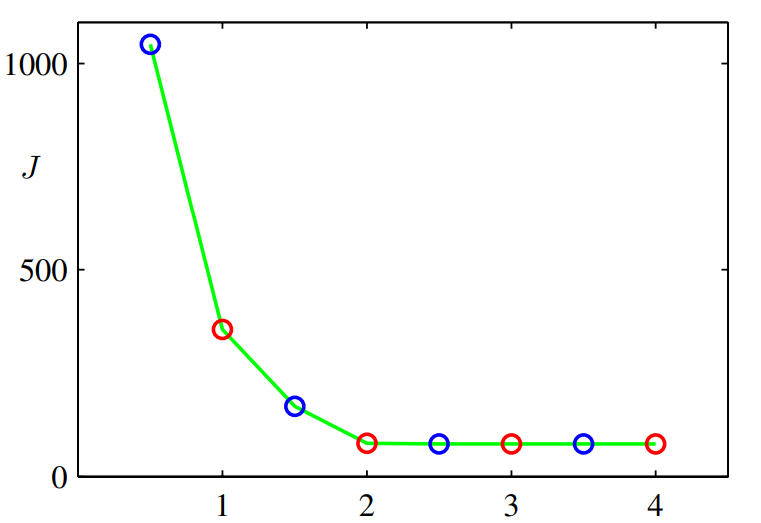
파란색 점은 E step, 빨간색 점은 M step을 나타냅니다. 위에서 진행한 k-means algorithm에 의해 J의 값이 점점 줄어드는 것을 알 수 있습니다.
k-means algorithm의 주목할만한 점은 모든 data point는 유일하게 하나의 cluster로 할당된다는 점입니다. 한편, 어떤 data point는 cluster의 중심들 중간에 위치할 수도 있습니다. 이때는 이와 같은 hard assignment가 좋은 방법이 아닙니다. 따라서 probabilistic formulation을 구성해서 k번째 cluster에 대한 data point의 불확정성을 고려해 soft assignment를 적용할 수 있습니다.
9.1.1 image segmentation
K-means algorithm을 활용해서 image segmentation and image compression 문제를 해결할 수 있습니다. segmentation의 목적은 image를 같은 시각 정보를 가진 objects를 여러 영역으로 나누는 것에 있습니다. 모든 이미지에 있는 픽셀은 R, G, B의 강도로 구성된(0과 1사이의 값) 3차원의 공간으로 구성되어 있습니다. 우리의 segmentation은 모든 픽셀을 data points로 취급해서 어려움 없이 K-means algorithm을 적용할 수 있습니다. center 를 {R, G, B}의 강도로 생각할 수 있습니다. 이미지 segmentation을 위해 오로지 K개의 색깔만을 사용하는 것을 알 수 있습니다. 아래의 그림은 다양한 K에 대한 image segmentation의 결과를 보여줍니다.

9.2. Mixtures of Gaussians
single Gaussian보다 선형 중첩(linear superposition)을 활용한 Gaussian mixture model은 더 풍성한 density models임을 알 수 있습니다. 이제 우리는 Gaussian mixtures를 discrete latent variables에 대해 나타내려고 합니다. 이 방식은 important distribution에 대한 더욱 훌륭한 직관을 제공해줍니다. 또한, expectation-maximization의 동기 부여로 이어집니다.
선형 중첩을 고려해 아래와 같은 식을 생각해볼 수 있습니다.
그 뒤, K 차원의 binary random variable을 z를 생각합니다. z는 1-of-K representation을 가정하고 있습니다. 따라서 z의 원소 과 을 만족합니다. 이때, 다음과 같이 를 연관을 지어 생각할 수 있습니다.
비슷하게 z에 대한 x의 조건부 확률을 아래의 가우시안 분포로 생각할 수 있습니다.
가능한 모든 z에 대한 p(z)p(x|z)의 summation으로 p(x)를 얻을 수 있습니다.
위의 과정을 통해 latent variable z를 포함하는 Gaussian mixture 수식을 찾았습니다. 이제, 우리는 marginal distribution p(x) 대신 joint distribution p(x, z)을 사용할 수 있게 되었습니다. 이제 expectation-maximization algorithm을 적용해 볼 수 있습니다.
중요한 다른 quantity로 z given x의 조건부 확률을 생각해볼 수 있습니다. 를 로 표기합니다. Bayes’ theorem을 활용하면 다음을 얻어낼 수 있습니다.

는 x를 관찰하고 나서 그에 대응되는 posterior probability로 생각할 수 있습니다. 는
observation x에 대한 component k의 responsibility로 볼 수 있습니다. 아래의 예시를 살펴보면서 직관적인 정리를 해볼 수 있습니다.

3개로 구성된 Gaussian mixture에서 500개의 points를 샘플링 한 상황을 나타냅니다.
(a) joint distribution p(z)p(x|z)를 참고하여 색깔을 구분한 그림입니다.
(b) marginal distribution p(x)를 구해 색깔로 나타냈습니다.
(c) responsibilities 를 고려해 mixing 된 색깔을 나타냈습니다.
위의 예시를 살펴보면서 (a)는 hard assignment (c)는 soft assignment를 뚜렷이 구분할 수 있습니다.
9.2.1 Maximum likelihood
GMM을 활용해 log likelihood를 아래와 같이 표현할 수 있습니다.

잠깐! singularities!
위의 함수를 어떻게 하면 최대화 할 수 있을지 알아보기 전에 maximum likelihood framework를 GMM에 적용했을 때, 문제가 생기는 singularities를 짚고 넘어가야 합니다.
1) cluster에 data가 하나만 할당된 경우
간편함을 위해, 라고 가정해봅니다. j 번째 component가 하나의 data point를 원소로 가지고 이때의 평균을 로 생각해봅니다. 이때, 에 대해 아래의 term을 만족합니다.
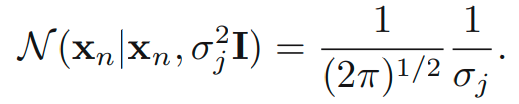
문제는 이 되면 무한대로 발산하여 log likelihood 함수 역시 무한대로 발산하게 됩니다.
이 문제를 해결하기 위해서 heuristics를 적용해볼 수 있습니다. 만약 Gaussian component가 collapsing 되는 것을 감지했을 때, random 하게 mean을 재설정한 뒤 optimization을 계속 진행하는 것입니다.
2) permutation 중복
K개의 mixture model은 총 K! 개의 중복된 모델이 있습니다. 이 문제는 identifiability 라는 명칭을 별도로 가지고 있습니다.
9.2.2 EM for Gaussian mixtures
maximum likelihood(latent variables를 포함하는) solutions를 찾기 위한 우아한 방법으로 expectation-maximization algorithm을 생각할 수 있습니다.
1) optimization with respect to
위에서 얻은 을 로 미분했을 때 Gaussian components를 0으로 만드는 조건을 우선으로 생각해봅니다.



를 cluster k에 할당된 유효한 data points의 개수라고 생각할 수 있습니다. 위의 식에서 볼 수 있듯이 는 k번째 Gaussian component에 대한 weighted mean이라고 생각할 수 있습니다. 이때의 weight는 posterior probability 입니다.
2) optimization with respect to
마찬가지로 에 대해서 maximum likelihood solution을 구하면 아래와 같습니다.

이는 posterior probability를 weight로 하는 weighted covariance의 식으로 생각해볼 수 있습니다. 분모는 마찬가지로 k번째 component로 할당되는 유효한 data point의 개수로 생각해볼 수 있습니다.
3) optimization with respect to
는 constraint를 고려해줘서 optimization을 진행해야됩니다. Lagrange multiplier를 활용해서 다음 quantity를 maximize할 수 있습니다.

이를 에 대해서 미분한 뒤 0 이 되는 식은 다음과 같습니다.

의 합이 1이라는 것을 알면 λ = −N임을 알 수 있습니다. 이를 활용해서 다시 식을 재정비하면 다음과 같습니다.

위의 1), 2), 3)의 결과에서 주목해야 할 점은 closed-form solution이 아니라는 것입니다. 그 이유는 가 parameters에 의존적이기 때문입니다. 하지만, maximum likelihood problem을 풀기 위해 iterative scheme을 활용할 수 있습니다. 이는 모두 EM 알고리즘의 한 예시임을 알 수 있습니다.
E(expectation) step: posterior probabilities(responsibilities)를 계산합니다.
M(maximization) step: E step의 결과를 통합시켜 means, covariances 그리고 mixing coefficients를 재평가합니다.
아래의 예시를 보며 Gaussian mixtures에서 EM을 어떻게 활용할 수 있는지 살펴봅시다.
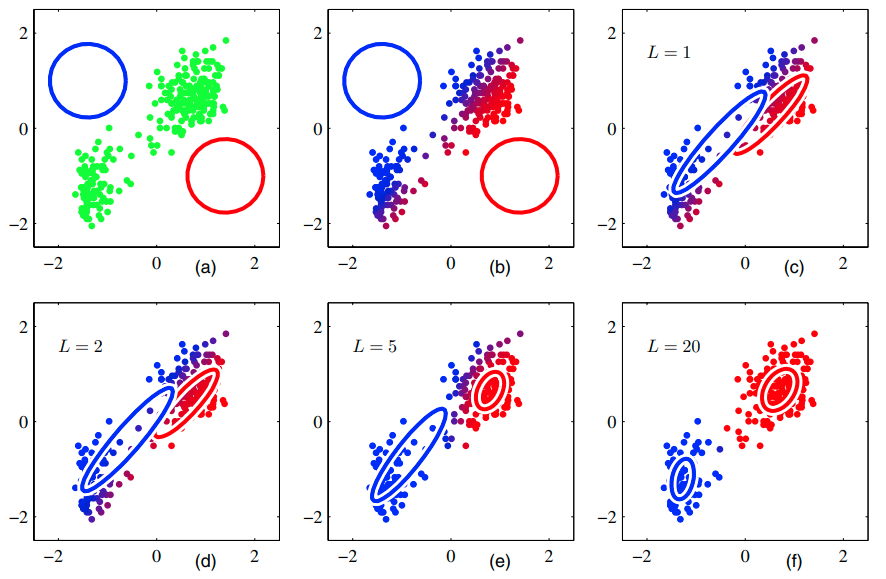
(a) data points는 초록색으로, 가우시안 컴포넌트는 빨간색, 파란색의 원으로 표현했습니다.
(b) 첫 번째 E step의 결과를 묘사하고 있습니다. data point에 해당하는 posterior probability를 파란색과 빨간색 사이의 색으로 표현했습니다.
(c) 첫 번째 M step의 결과를 나타내고 있습니다. (b) 의 blue cluster의 weighted mean을 계산하여 파란색 원의 좌표가 이동한 것을 볼 수 있습니다.
(d) 2회 EM을 진행한 뒤의 결과
(e) 5회 EM을 진행한 뒤의 결과
(f) 20회 EM을 진행한 뒤의 결과
수렴하기 위해 EM algorithm은 K-means algorithm에 비해서 더 많은 반복을 필요로 합니다. 각 cycle은 더 많은 computation이 필요합니다. 따라서 K-means algorithm을 활용해 EM의 초깃값을 구하는 것이 일반적입니다. covariance matrices는 K-means algorithm으로 찾은 sample covariances로 간편히 초기화할 수 있고 mixing coefficients는 각 클러스터에 data points가 할당된 비율을 활용해 설정할 수 있습니다. log likelihood를 maximize 하는 gradient-based 접근 방식은 Gaussian component collapses가 발생하지 않도록 주의해야 합니다. log likelihood의 극대점이 여러 개 존재할 수 있으므로 EM은 가장 최고의 해답을 제시해주지 않는다는 것을 알아두셔야 합니다.
EM 알고리즘을 아래에 요약했습니다.
1) , 와 를 초기화하고 log likelihood의 초기값을 계산합니다.
2) E step: 현재의 parameters를 활용해 responsibilities의 값을 계산합니다.
3) M step: 현재의 responsibilities를 활용해 parameters를 재평가합니다.
4) log likelihood를 계산하고 parameters 혹은 log likelihood의 수렴성을 체크합니다. 수렴하지 않을 경우 2)로 돌아갑니다.
9.3. An Alternative View of EM
우리는 observation X와 그에 해당하는 latent variable Z에 대해 {X, Z}를 complete data set이라고 부릅니다. X만 관찰했을 때는 incomplete로 나타냅니다. complete data set에 대한 likelihood는 으로 나타낼 수 있습니다. 이를 최대화하는 작업이 더욱 더 직관적임을 알 수 있습니다.
통상적으로, complete data set이 주어지는 경우는 드뭅니다. 따라서 Z에 관한 값은 오로지 posterior distribution인 를 활용해서 구할 수 있습니다. 우리는 complete data에 대한 log-likelihood를 얻을 수 없으므로 E step에서 얻어진 posterior distribution의 기댓값으로 대신할 수 있습니다. 이후의 M step에서는 기댓값을 최대화할 수 있습니다. 다음과 같이 notion을 정의합니다.
: parameters에 대한 현재 estimate
: E and M steps을 번갈아 시행하고 난 뒤에 개선된 estimate
E step에서 우리는 을 활용해 posterior distribution 을 구합니다. 그 뒤, posterior distribution을 활용해 complete-data log likelihood의 기댓값을 구할 수 있습니다. 이를 으로 표현하고 수식은 아래와 같습니다.
M step에서 아래의 maximization의 방식으로 를 구할 수 있습니다.
General EM 알고리즘을 아래에 요약했습니다.
1) 의 초기화합니다.
2) E step: 을 계산합니다.
3) M step: 를 계산합니다.
4) , log likelihood 혹은 parameter values의 수렴성을 판단합니다. 만약 수렴하지 않는다면 2)로 돌아갑니다.
9.3.1 Gaussian mixtures revisited
complete data set {X, Z}에 대해 likelihood를 최대화 하는 문제를 고려해봅니다.
다시 한 번, Lagrange multiplier을 위의 식에 적용해서 미분과 제한 조건을 활용하면 아래의 식을 얻어낼 수 있습니다.

한편, 의 기댓값은 아래의 식을 만족합니다.

따라서 complete-data log likelihood의 기댓값은 아래의 식을 만족합니다.
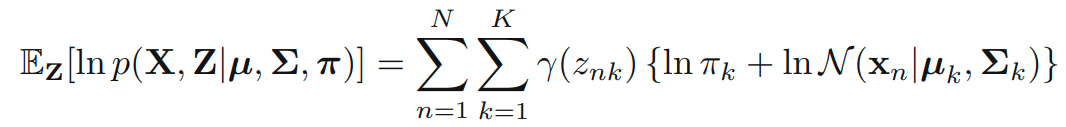
이 식을 활용한 EM 알고리즘은 이전에 유도한 Gaussian mixtures에서의 예시의 더 정확한 증명입니다.
9.3.2 Relation to K-means
K-means algorithm은 hard assignment의 방식을 사용하고 있는데, 반해 EM algorithm은 posterior probabilities에 기반한 soft assignment의 방식을 사용하고 있습니다. 아래의 방식으로 EM의 극한을 활용해 K-means algorithm을 유도할 수 있습니다.
주어진 Gaussian mixture model의 covariance matrices를 라고 생각해봅니다. 이때 아래의 식이 성립합니다.
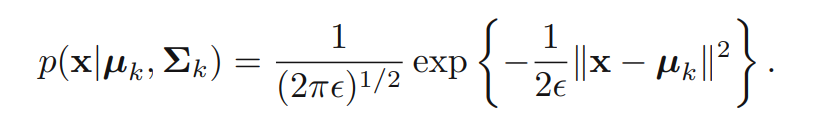
이제 EM 알고리즘을 적용해봅니다. 은 고정점으로 취급합니다. 에 대한 responsibilities는 다음과 같습니다.
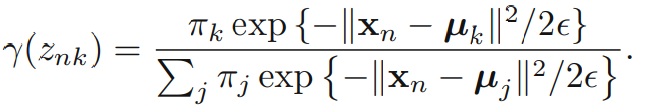
→ 0이면 임을 알 수 있습니다. 그 이유는 → 0일 때, 의 분모의 지배적인 항은 이 가장 최소가 될 때입니다. 그때의 j를 i라고 하면 은 일 때 1이 되고 나머지에서는 0이 된다는 것을 알 수 있습니다. 이때의 complete-data log likelihood의 기댓값은 아래의 식을 만족합니다. 이는 앞서 봤던 K-means clustering의 objective 함수를 최적화하는 것과 완전히 같습니다.

9.3.3 Mixtures of Bernoulli distributions
지금까지 우리는 가우시안을 설명하는 연속적인 변수들을 집중적으로 다루었습니다. EM algorithm을 다른 문맥에서 살펴보고자 합니다. discrete binary variables을 다루기 위해 Bernoulli distributions를 도입합니다. 이 모델은 latent class analysis이라고도 불립니다.
D개의 binary variable 를 생각해봅니다. 이들은 를 매개변수로 하는 Bernoulli distribution의 지배를 받습니다. 에 대해 다음 식이 성립합니다.

위의 분포에 대한 평균과 공분산은 아래와 같습니다.

이번엔 아래와 같은 분포를 생각해봅니다.

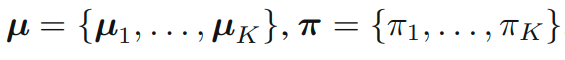

이 분포에 대한 평균과 공분산은 아래와 같습니다.


data set {}이 주어졌을 때, 위 모델에 대한 log likelihood 함수는 아래와 같습니다.
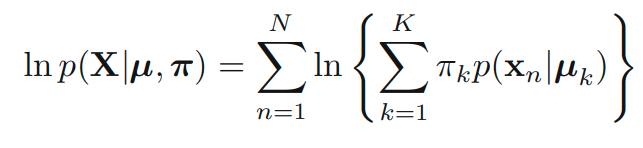
위의 식에서 볼 수 있다시피, 로그함수 내부에 합의 수식이 포함되어 있으므로 이는 closed form이 아님을 알 수 있습니다. 여기서 likelihood 함수를 최대화하는 EM 알고리즘을 유도해봅시다. 이를 위해서 각 x와 연관된 명시적인 latent variable z를 생각합니다. 는 one-hot encoding 되어 있는 variable입니다. latent variable을 적용해서 아래와 같이 conditional distribution을 생각할 수 있습니다.
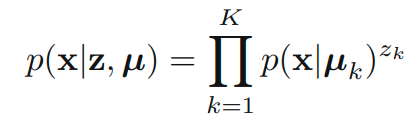
prior distribution은 아래와 같습니다.
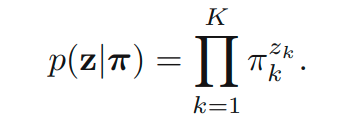
EM 알고리즘을 유도해내기 위해 complete-data log likelihood를 파악합니다.

여기서 입니다. 다음으로 위의 식의 기댓값을 구하면 아래와 같습니다.


E step에서는 Bayes 정리를 활용해 responsibilities를 구합니다.
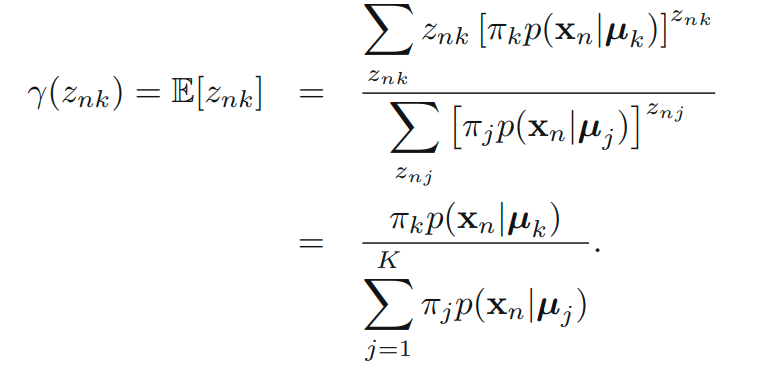
그 뒤, 최적화 작업을 거치면 아래의 식들을 얻을 수 있습니다.
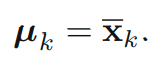


위의 그림은 2, 3, 4만을 포함하는 image data set을 활용해 위의 Bernoulli mixture model을 활용한 케이스입니다. 첫 그림은 0.5를 경계로 gray scale로 그림을 변환한 것을 나타내고 있습니다. 아래쪽의 첫 3개의 그림은 각 클러스터의 mean value()를 그림으로 나타낸 것입니다. 이때, k는 3개이고 i는 픽셀의 개수만큼 존재합니다.
9.4. The EM Algorithm in General
expectation maximization 알고리즘은 latent variable을 가지는 확률 모델에서 maximum likelihood solutions를 찾는 일반적인 알고리즘입니다. 이 장에서는 그동안 앞의 내용에서 heuristic 하게 다뤘던 내용에 대한 증명과 일반적인 방법론을 제시합니다.
observed variable X와 hidden variable Z를 가지고 probabilistic model을 고려해봅시다. joint distribution 은 parameter θ의 지배를 받습니다. 우리의 목표는 아래의 likelihood를 최대화하는 것입니다.

여기선 Z를 discrete 하다고 생각합니다. Z를 continuous 하다고 생각할 때 summation을 적분으로 치환해서 생각해주면 되기 때문에 일반성을 잃지 않고 discrete인 경우만 다룹니다. 직접 을 최적화하는 것은 힘들기 때문에 complete-data likelihood 함수인 을 최적화합니다. Z가 분포 q(Z)를 따른다고 가정합니다.

한편 KL divergence는 0 이상의 값을 가지므로 는 를 lower bound로 가집니다.
EM algorithm은 maximum likelihood 해를 찾기 위한 반복적인 두 단계의 optimization 기술을 활용합니다. 식을 활용해 EM 알고리즘이 실제로 최적화를 하고 있는지에 대한 여부를 증명할 수 있습니다.
E step에서는 가 고정된 상태에서 를 에 대해서 maximize 합니다. 한편, 는 에 의존적이지 않습니다. 따라서, 은 이 0일 때 가장 최대의 값이 됩니다. Kullback-Leibler divergence의 등호 성립조건은 입니다. 이때의 lower bound는 log likelihood와 같게 됩니다.
M step에서는 가 고정된 상태에서 이 에 대해 최대화 되어 새로운 값 를 생성합니다. 이는 곧 log likelihood 함수를 더 크게 만들 수 있습니다. 여기서 distribution q는 에 관한 함수이므로 KL divergence는 0이 아님을 알 수 있습니다. 따라서 아래의 식이 성립합니다.

이때, optimization variable은 임을 알 수 있습니다. 따라서 을 적당히 선택해 optimize 하는 것이 핵심입니다.

위의 그래프를 활용해 지금까지의 과정을 좀 더 직관적으로 바라볼 수 있습니다. 빨간색의 커브가 log likelihood 함수입니다. 가장 먼저 로 E step을 시작합니다. E step에서는 latent variables의 분포를 계산하는데 이는 곧 을 알 수 있게 해줍니다. 그래프에서 볼 수 있다시피 L은 convex이며 에서 log likelihood와 접하고 있습니다. M step에서는 가 최대가 되는 를 찾아냅니다. 이 과정을 log likelihood가 수렴할 때까지 계속해서 반복해 나갑니다.
마치며,
혼합 가우시안 모델을 활용한 최적화 작업의 맥락에서 k-means clustering과 EM이 비슷하다는 것을 알게 되어 좀 더 EM을 insightful 하게 바라 볼 수 있게 된 것 같습니다. 예전에 기계학습 수업을 들었을 때도 soft, hard assignment의 차이를 느끼며 감탄한 적이 있었는데 이번에도 역시 숨기지 못했습니다. 아무튼 드디어! CPD를 공부할 준비가 되었다는 것에 안심이 되네요!