NERF 코드 분석 1.load_blender 그리고 동차 좌표계

코드짜는침팬지·2023년 9월 16일

DIP NeRF 동차 좌표계 파이썬

학부 연구생

목록 보기

1/10

4학년 졸업논문 주제 겸 기업 프로젝트 겸 연구실 인턴으로 진행중

일단 NERF-pytroch 분석부터 시작하는게 맞는거 같아서
nerf-pytorch는 다음과 같은 구조로 이루어져 있다.

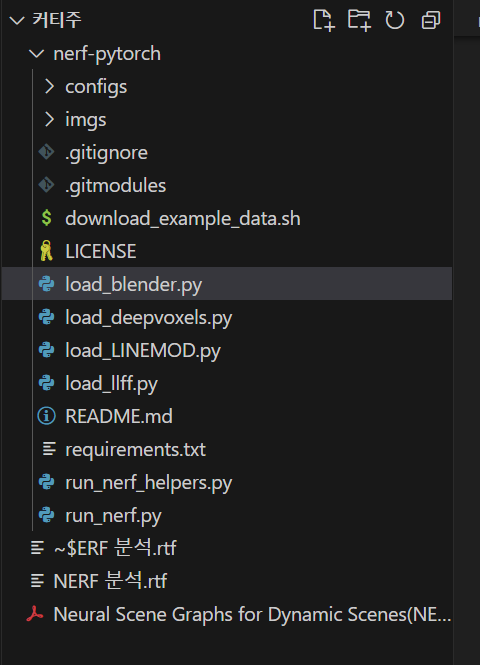
load_blender: Blender에서 생성된 데이터셋을 로드하는 함수

load_deepvoxels: DeepVoxels 형식의 데이터를 로드하는 함수

load_LINEMOD: LINEMOD 3D 객체 인식을 위한 데이터셋

load_llff: LLFF (Local Light Field Fusion) 빛의 광선을 표현

run_nerf_helpers: 이 파일은 NeRF 알고리즘을 실행하는 데 필요한 다양한 도우미 함수

run_nerf: 이 파일은 NeRF 알고리즘의 주 실행 코드를 포함하며, 훈련 및 테스트를 위한 주요 함수와 파이프라인

load_blender

load_blender.py는 Blender에서 생성된 데이터를 로드하고 처리하는 코드를 포함하고 있다.
Blender는 3D 컴퓨터 그래픽스 소프트웨어로, 3D 모델링, 애니메이션,
렌더링 등의 작업을 수행할 수 있는데,

NeRF에서는 Blender를 사용하여 합성된 데이터셋을 생성하고 이를 학습 및 테스트에 사용한다.

일단 4x4 행렬을 쓰는 이유를 먼저 알아보자,
예전에 학교에서 진행한 cylinder robot의 kalman filter 처리에서도
4x4 행렬이 나왔는데 4x4행렬과 3D 렌더링의 상관관계는 다음과 같다.

이를 이해하기 위해선 일단 동차 좌표계(Homogeneous Coordinates),
프로젝티브 변환(projective transform) 에 대한 이해가 좀 필요하다.

동차 좌표계 (homogeneous coordinates)

좌표를 확장해서 추가적인 차원을 포함시키는 것 이다.
예를들어, 2D 좌표 $[x, y]$ 는 동차 좌표계에서
3D 좌표 $[x, y, w]$ 로 확장될 수 있으며,
3D 좌표 $[x, y, z]$ 는 4D좌표 $[x, y, z, w]$ 로 확장된다.
4D라고 하니까 갑자기 잘 이해가 안간다.
우리는 3차원 세계에 살고 있는데 왜 4D라는 단어가 나올까?

이건 그냥 가중치(weight) w 를 추가해서
3차원을 조금 더 편하게 표현하기 위한 도구라 보면 된다.

동차 좌표계의 장점:

이동 변환의 간소화:
동차 좌표계를 사용하면 이동, 회전, 스케일링 등의 변환을 하나의 행렬 곱셈으로 표현할 수 있다. 특히, 이동 변환은 비동차 좌표계에서는 행렬 곱셈으로 표현할 수 없지만, 동차 좌표계에서는 이것이 가능하다.

원점에서 무한대까지의 표현:
w의 값이 0일 때, 동차 좌표는 무한대에 있는 점을 나타낸다. 이는 원근 투영과 같은 그래픽스 변환에서 유용하다.

프로젝티브 변환(projective transform):
동차 좌표계는 프로젝티브 공간에서의 변환을 표현하는 데 유용한데, 이는 카메라 투영과 같은 그래픽스 및 비전 작업에서 중요하게 쓰인다.

동차 좌표계에서의 변환:
동차 좌표계에서의 변환은 행렬 곱셈을 사용하여 수행됩니다. 예를 들어, 3D 공간에서의 이동 변환은 다음과 같은 4x4 행렬을 사용하여 표현됩니다:

동차 좌표계에서 w 값은 좌표의 스케일 또는 가중치를 나타낸다.
이게 뭔지 조금 더 자세히 알아보자.

w의 값에 따라 동차 좌표 [x, y, z, w]의 실제 3D 좌표는 [x/w, y/w, z/w]로 변환된다.

w = 0일 때: 이 좌표는 무한대를 나타낸다. 실제 3D 좌표로 변환할 수 는 없고, 이러한 좌표는 프로젝티브 변환에서 특별한 의미를 가진다.

조금 더 자세하게 말해보자면
동차 좌표계에서 ( w ) 값이 0일 때, 해당 좌표는 "무한대에 있는 점"을 나타내고,

프로젝티브 기하학에서, 무한대에 있는 점들은 "극한점" 또는 "무한점"이라고 불린다.

이러한 점들은 유한한 공간에서는 직접적으로 표현할 수 없지만, 동차 좌표계를 사용하면 이러한 점들을 표현하고 계산할 수 있게 된다.

예를 들어, 2D 평면에서 직선의 방정식을 생각해보자. 두 직선이 평행하다면, 이 두 직선은 유한한 공간에서는 절대 교차하지 않는다. 그러나 프로젝티브 기하학에서는 이 두 직선은 무한대에서 만난다고 간주된다.
이 "무한대에서의 교차점"은 동차 좌표계에서 ( w = 0 )인 점으로 표현됩니다.

이러한 개념은 컴퓨터 그래픽스, 컴퓨터 비전, 로보틱스 등에서 카메라 투영과 같은 변환을 다룰 때 중요하게 사용되는데,
동차 좌표계를 사용하면, 무한대에 있는 점들을 포함하여 다양한 기하학적 변환을 일관되고 효율적인 방식으로 표현하고 계산하는것이 가능해진다.

w = 0.5일 때: 동차 좌표 [x, y, z, 0.5]는 실제 3D 좌표로 [2x, 2y, 2z]로 변환됩니다. 즉, 원래의 좌표보다 2배 멀리 떨어진 위치를 나타낸다.
w = 1일 때: 동차 좌표 [x, y, z, 1]는 실제 3D 좌표로 [x, y, z]로 변환됩니다. 이는 동차 좌표계에서 가장 일반적인 경우로, 원래의 좌표를 그대로 나타낸다.

따라서 w 값은 좌표의 스케일 또는 위치를 조절하는 데 사용된다. w가 0에 가까울수록 해당 좌표는 무한대에 가까워진다. w가 1일 때는 원래의 좌표를 나타내며, w가 그보다 크거나 작을 때는 좌표가 스케일링된다.

자 이게 무슨 말이냐, 결국 다 선형대수다. 실제로 간단하게 써보면서 이해 해보도록 하자.

다음과 같은 행렬이 있다고 가정하자

이동 변환 행렬:

\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \\ \end{bmatrix}

점 ([x, y])를 동차 좌표로 표현 시:

\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}

이동 변환 행렬을 사용하여 점을 이동:

\begin{bmatrix} 1 & 0 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \\ \end{bmatrix} \times \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}= \begin{bmatrix} x + 3 \\ y + 2 \\ 1 \\ \end{bmatrix}

결과적으로, 점 $[x, y]$ 는 $[x + 3, y + 2]$ 로 이동된다.

$3\times3$ 행렬로 다시 한 번 복습해보자.
3D 공간에서의 점을 $[x, y, z]$ 라고 가정하자.

이때 이동 변환 행렬은:

\begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}

이 행렬을 동차 좌표 $[x, y, z, 1]$ 에 곱하면:

\begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \times \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}= \begin{bmatrix} x + t_x \\ y + t_y \\ z + t_z \\ 1 \\ \end{bmatrix}

결과적으로, 점 $[x, y, z]$ 는 $[x + t_x, y + t_y, z + t_z]$ 로 이동된다.

프로젝티브 변환(projective transform)

프로젝티브 변환은 2D 또는 3D 공간의 점들을 다른 2D 또는 3D 공간으로 매핑하는 변환이다. 이 변환은 특히 이미지와 3D 장면 간의 관계를 표현할 때 중요하다.
카메라 투영이 프로젝티브 변환의 일반적인 예이다.

기본 개념:

프로젝티브 변환은 선의 접점을 보존하는 변환이다.
즉 두 선이 한 점에서 교차하면 변환 후에도 두 선이 교차하는 것을 의미한다.

2D 프로젝티브 변환:

2D 프로젝티브 변환은 2D 이미지에서 2D 이미지로의 매핑을 나타낸다. 이 변환은 3x3 행렬을 사용하여 표현한다.

예를 들어보자

카메라가 평면에 투영하는 경우를 생각해보자.
이 투영은 2D 프로젝티브 변환으로 모델링될 수 있다.

프로젝티브 변환 행렬:

P = \begin{bmatrix} p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23} \\ p_{31} & p_{32} & 1 \end{bmatrix}

이 행렬을 사용하여 2D 점 ([x, y])를 변환하려면, 먼저 동차 좌표로 확장하여 ([x, y, 1])로 표현하고, 이를 행렬 (P)와 곱한다.

3D 프로젝티브 변환:

3D 프로젝티브 변환은 3D 공간에서 2D 이미지로의 매핑을 나타낸다.
이 변환은 4x4 행렬을 사용하여 표현된다.

예를 들어보자,
3D 장면에서 객체의 점을 2D 이미지 평면에 투영하는 경우를 생각해보자.
이 투영은 3D 프로젝티브 변환으로 모델링될 수 있다.

프로젝티브 변환 행렬:

P = \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \\ 0 & 0 & 0 & 1 \end{bmatrix}

이 행렬을 사용하여 3D 점 $[x, y, z]$ 를 변환하려면, 먼저 동차 좌표로 확장하여 $[x, y, z, 1]$ 로 표현하고, 이를 행렬 $P$ 와 곱한다.

프로젝티브 변환의 강점은 카메라의 내부 및 외부 파라미터, 렌즈 왜곡 등을 고려하여 정밀하게 조정할 수 있다는 점이다.

자, 이제 코드를 분석하기위해 필요한 사전 지식이 마련되었으니 분석 해보자.

import os
import torch
import numpy as np
import imageio 
import json
import torch.nn.functional as F
import cv2


trans_t = lambda t : torch.Tensor([
    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,t],
    [0,0,0,1]]).float()

rot_phi = lambda phi : torch.Tensor([
    [1,0,0,0],
    [0,np.cos(phi),-np.sin(phi),0],
    [0,np.sin(phi), np.cos(phi),0],
    [0,0,0,1]]).float()

rot_theta = lambda th : torch.Tensor([
    [np.cos(th),0,-np.sin(th),0],
    [0,1,0,0],
    [np.sin(th),0, np.cos(th),0],
    [0,0,0,1]]).float()


def pose_spherical(theta, phi, radius):
    c2w = trans_t(radius)
    c2w = rot_phi(phi/180.*np.pi) @ c2w
    c2w = rot_theta(theta/180.*np.pi) @ c2w
    c2w = torch.Tensor(np.array([[-1,0,0,0],[0,0,1,0],[0,1,0,0],[0,0,0,1]])) @ c2w
    return c2w

위의 함수는 동차행렬을 이용한 transformation matrix 다.

Transformation Matrices:

trans_t(t): t만큼의 z-축 이동 변환 행렬을 생성한다.
rot_phi(phi): phi 각도만큼의 x-축 회전 변환 행렬을 생성한다.
rot_theta(th): th 각도만큼의 y-축 회전 변환 행렬을 생성한다.

pose_spherical(theta, phi, radius):
주어진 각도와 반지름을 사용하여 구 형태의 포즈 변환 행렬을 생성한다.

포즈 변환 행렬에 대해 간단하게 설명하자면 다음과 같다.

Pose Transform:

Pose는 객체나 카메라의 위치와 방향을 나타내는 정보다.
Pose Transform은 한 좌표계에서의 점이나 벡터를 다른 좌표계로 변환하는 것을 의미한다.
이 변환은 주로 이동(translation)과 회전(rotation)으로 구성되는데,

Pose Transform을 표현하는 가장 일반적인 방법이
4x4 동차 변환 행렬을 사용하는 것이다 (위에 동차행렬을 설명 한 이유)

T = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix}

여기서:

( R )는 3x3 회전 행렬이다.
( t )는 3x1 이동 벡터다.

예를 들어보자:

카메라가 x축 방향으로 1 단위, y축 방향으로 2 단위 이동하고,
z축을 중심으로 90도 회전한다고 가정해보자.
이 경우의 Pose Transform 행렬은 다음과 같다:

$T = \begin{bmatrix} 0 & -1 & 0 & 1 \\ 1 & 0 & 0 & 2 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

이 식이 어떻게 나왔는지 조금 더 자세히 설명 해보자면

회전 변환은 주로 삼각함수를 사용하여 표현된다.
(선형대수를 시작으로 로보틱스,정역학,동역학, 영상처리등 에서 널리 쓰이는 지식이다)

3D 공간에서의 회전은 주로 3개의 주축 (x, y, z) 중 하나를 중심으로 이루어진다.

Z축을 중심으로의 회전:

각도 $\theta$ 만큼 Z축을 중심으로 회전할 때, 회전 행렬은 다음과 같다:
$R_z(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}$
Y축을 중심으로의 회전:
$R_y(\theta) = \begin{bmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{bmatrix}$
X축을 중심으로의 회전:
$R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) \\ 0 & \sin(\theta) & \cos(\theta) \end{bmatrix}$

예를 들어, Z축을 중심으로 90도 $(또는 \pi/2)$ 회전하면:

R_z(\pi/2) = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}

이 행렬을 사용하여 3D 점을 회전시키면, 해당 점은 Z축을 중심으로 90도 회전하게 된다.

def load_blender_data(basedir, half_res=False, testskip=1):
    splits = ['train', 'val', 'test']
    metas = {}
    for s in splits:
        with open(os.path.join(basedir, 'transforms_{}.json'.format(s)), 'r') as fp:
            metas[s] = json.load(fp)

    all_imgs = []
    all_poses = []
    counts = [0]
    for s in splits:
        meta = metas[s]
        imgs = []
        poses = []
        if s=='train' or testskip==0:
            skip = 1
        else:
            skip = testskip
            
        for frame in meta['frames'][::skip]:
            fname = os.path.join(basedir, frame['file_path'] + '.png')
            imgs.append(imageio.imread(fname))
            poses.append(np.array(frame['transform_matrix']))
        imgs = (np.array(imgs) / 255.).astype(np.float32) # keep all 4 channels (RGBA)
        poses = np.array(poses).astype(np.float32)
        counts.append(counts[-1] + imgs.shape[0])
        all_imgs.append(imgs)
        all_poses.append(poses)
    
    i_split = [np.arange(counts[i], counts[i+1]) for i in range(3)]
    
    imgs = np.concatenate(all_imgs, 0)
    poses = np.concatenate(all_poses, 0)
    
    H, W = imgs[0].shape[:2]
    camera_angle_x = float(meta['camera_angle_x'])
    focal = .5 * W / np.tan(.5 * camera_angle_x)
    
    render_poses = torch.stack([pose_spherical(angle, -30.0, 4.0) for angle in np.linspace(-180,180,40+1)[:-1]], 0)
    
    if half_res:
        H = H//2
        W = W//2
        focal = focal/2.

        imgs_half_res = np.zeros((imgs.shape[0], H, W, 4))
        for i, img in enumerate(imgs):
            imgs_half_res[i] = cv2.resize(img, (W, H), interpolation=cv2.INTER_AREA)
        imgs = imgs_half_res
        # imgs = tf.image.resize_area(imgs, [400, 400]).numpy()

        
    return imgs, poses, render_poses, [H, W, focal], i_split

load_blender_data(basedir, half_res=False, testskip=1):

Blender에서 생성된 데이터를 로드하는 함수다.
basedir: 데이터가 저장된 디렉토리 경로
half_res: 이미지의 해상도를 반으로 줄일지 여부를 결정하는 flag
testskip: 테스트 데이터를 로드할 때 건너뛸 프레임 수를 지정
함수는 이미지, 포즈, 렌더링 포즈, 카메라 매개변수, 데이터 분할 인덱스를 반환

Data Loading:
JSON 형식의 메타 데이터를 로드하여 트레이닝, 검증, 테스트 데이터를 처리한다.
각 프레임의 이미지와 변환 행렬을 로드한다.
카메라의 시야각을 기반으로 초점 거리를 계산한다.
render_poses: 특정 각도와 거리를 사용하여 렌더링 포즈의 시퀀스를 생성한다.
half_res: 이미지의 해상도를 반으로 줄이는 옵션이다.
필요한 경우 OpenCV의 cv2.resize 함수를 사용하여 이미지를 다운샘플링한다.

즉 코드는 Blender에서 생성된 데이터셋을 로드하고, 필요한 변환과 처리를 수행하여 NeRF 학습 및 테스트에 사용할 수 있는 형식으로 데이터를 반환한다.

코드짜는침팬지

학과 꼴찌 공대 호소인

다음 포스트