Ch.2 Image Pyramids & Frequency domain

Image Downsampling

Naive Image Downsampling

im[::2, ::2] → 한 픽셀씩 건너뛰기

▶ 해상도↓ 정보량↓ (=aliasing)

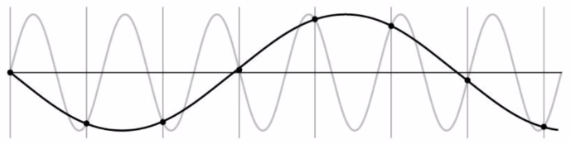
Aliasing

현실: 연속
이미지: discrete (or) sampled 된 현실

discrete (이산): 구별되고 별개의 값이나 상태를 가진 표현
→ (컴퓨터비전) 디지털 이미지의 픽셀값

sample (샘플): 특정 간격으로 연속 신호나 장면의 측정값을 취하여 표현

Sampling

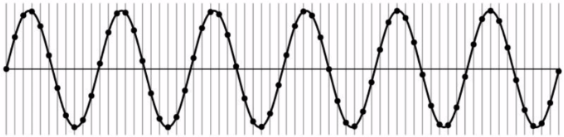
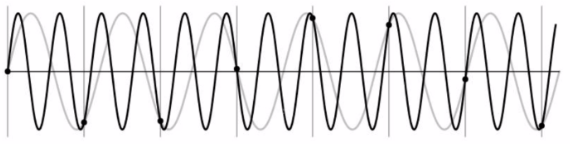
Under-sampling

정보의 손실:
더 낮은 주파수의 신호로 잘못 파악할 수 있다.

note
(언제나) 더 높은 주파수의 신호로 잘못 파악할 수 있다.

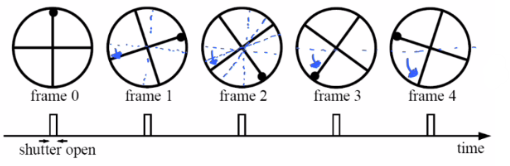
Temporal Aliasing

Anti-Aliasing

안티-에일리어싱 방법
1. over-sampling samples
2. 먼저 blur하고, 이후 샘플링

2번 방법
보통 가우시안 필터 사용

주파수↓ & 디테일↓ (정보가 손실되긴 함)
▶ 샘플링 덜 해도 괜찮아짐

Q1.
얼마나 blur 해야할까?

Q2.
얼마 단위로 샘플링 해야할까?

A.
Nyquist limit에 도달할 때까지

Gaussian Image Pyramid

길이: $\frac {1} {2}$ , 넓이: $(\frac {1}{2})^2$ → 길이: $(\frac {1} {2})^2$ , 넓이: $((\frac {1}{2})^2)^2$ → ...

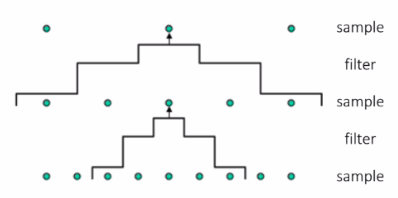
Constructing a Gaussian Pyramid

algorithm

repeat:
  filter
  subsample
(until min resolution reached)

Q.
전체 피라미드의 크기

A.
height: $1 + \frac {1}{2} + \frac {1}{2^2} + \frac {1}{2^3} + ...$
area: $1 + \frac {1}{2} + (\frac {1}{2})^2 + ((\frac {1}{2})^2)^2 + ...$

Some properties of the Gaussian pyramid

레벨이 높아질수록 blur (정보 손실됨)
→ 큰 디테일만 남음

▶ 더 높은 레벨로 복원 (upsampling) 불가능

Blurring is lossy

Residual 남겨두면 다시 업샘플링 가능

• downsampling 해버리면 $\frac {N} {2}$ 차원이 되어버려 연산(-) 불가능

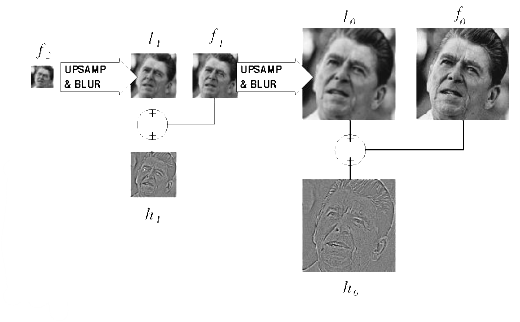
Laplacian Image Pyramid

Residual & 가장 윗 level 이미지 가지고 있으면 원본 이미지 복원 가능

bit 개수↓ & 값의 range 훨씬 적음
▶ 압축률↑

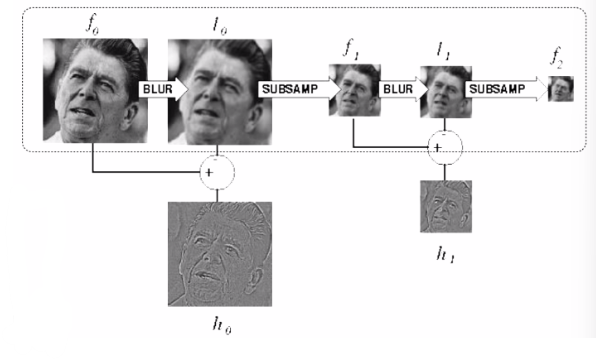
Constructing a Laplacian Pyramid

algorithm

repeat:
  filter
  compute residual
  subsample
(until min resolution reached)

Reconstructing the original image

algorithm

repeat:
  upsample
  sum with residual
(until original resolution reached)

Why is it called a Laplacian Pyramid?

Fourier Series

Basic building block

사인파 함수
$A*sin(\omega x + \phi)$

$A$: 진폭

• 주파수의 높이

$\omega$: 각주파수

• 시간 단위 Hz 내에서 사인파의 완전한 주기 횟수 - 속도 or 밀도)
• $\omega = 2\pi f$ ($f$: 사인파의 주파수)

$\phi$: 위상이동

• 원래 위치($\phi = 0$)일때, 수평으로 얼마나 이동하는지
• 양의 위상이동: 사인파를 왼쪽으로 이동시킴
• 음의 위상이동: 사인파를 오른쪽으로 이동시킴

Examples

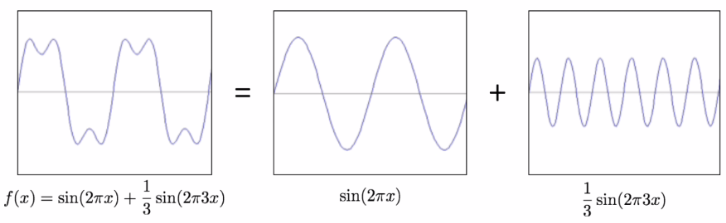
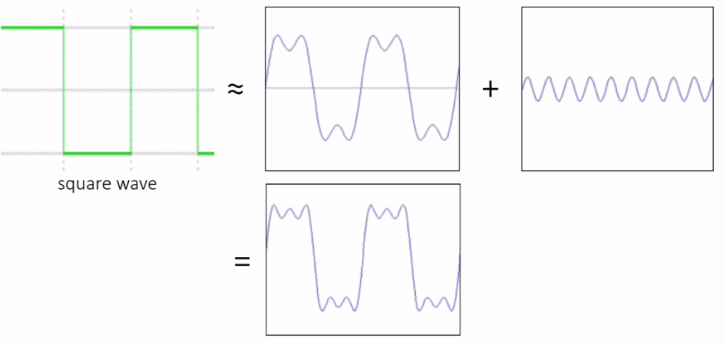
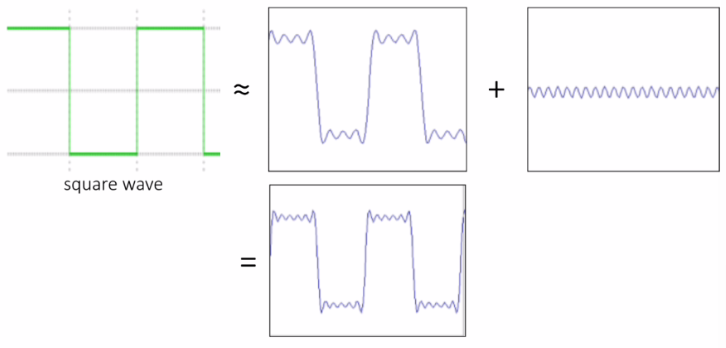
square wave $= A \sum_{k=1}^{\inf} \frac {1}{k} sin(2\pi kx)$

Frequency Domain

Visualizing the frequency spectrum

	$sin(2\pi kx)$	$\frac {1}{3} sin(2\pi 3kx)$
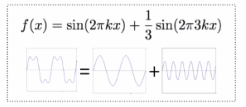
주파수	$k$	$3k$
증폭	$1$	$\frac {1}{3}$

Examples

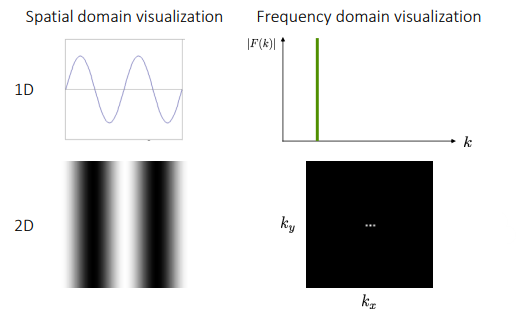
• 주파수: 계속 더해도 사라지지 않음.

Fourier Transform

Recalling some basics

Rectangular Coordinates
$R + jI$
$R$ : 실수 부분
$I$ : 허수 부분

▼
Alternative Reparameterization
▼

극 좌표계 (polar coordinates)

$r(cos \theta + j sin \theta)$

▼
(polar transform)
▼

$\theta = tan^{-1} (\frac {1} {R}) r = \sqrt {R^2 + I^2}$

지수 표기법 (exponential form)

$re^{j \theta}$

▼
(오일러 공식)
▼

$e^{j \theta} = cos \theta + j sin \theta$

Fourier Transform

Fourier Transform - continuous

$F(k) = \int_{\inf}^{-\inf} f(x)e^{-j2 \pi kx} dx$

Inverse Fourier Transform - continuous

$f(x) = \int_{\inf}^{-\inf} f(x)e^{j2 \pi kx} dx$

Fourier Transform - discrete

$F(k) = \frac {1}{N} \sum_{x=0}^{N-1} f(x)e^{-j2 \pi kx / N}$

$(k = 0, 1, 2, ..., N-1)$

Inverse Fourier Transform - discrete

$f(x) = \frac {1}{N} \sum_{x=0}^{N-1} f(x)e^{j2 \pi kx / N}$

$(x = 0, 1, 2, ..., N-1)$

Connection to the 'Summation of Sine Waves' idea

$f(x) = \sum_{k=0}^{N-1} F(k)e^{j2 \pi kx / N}$

▼
오일러 공식
$e^{j \theta} = cos \theta + j sin \theta$
▼

$f(x) = \sum_{k=0}^{N-1} F(k) \{cos(2 \pi kx) + jsin(2 \pi kx) \}$

Fourier Transform Pairs

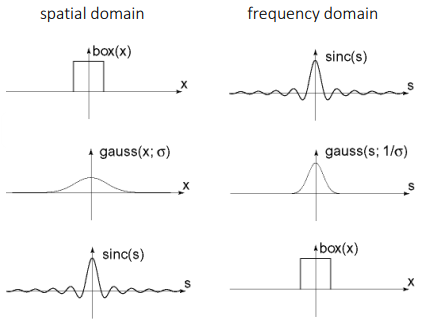
Fourier transform of natural images

Frequency-Domain Filtering

The convolution theorem

• 두 함수의 convolution의 푸리에변환 = 각 함수의 푸리에 변환의 곱
  $F(g*h) = F(g)F(h)$

• inverse도 마찬가지
  $F^{-1}(g*h) = F^{-1}(g) * F^{-1}(h)$

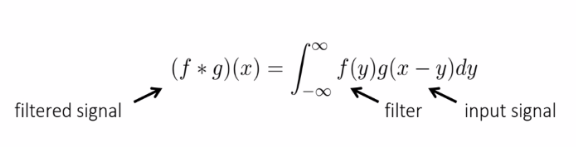
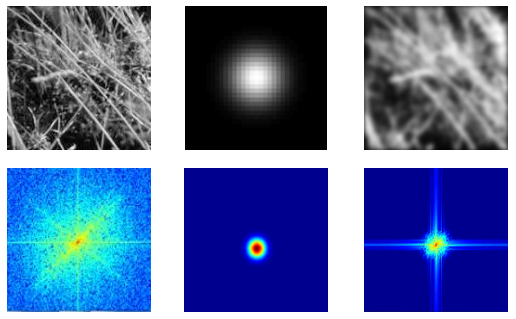
Spatial domain filtering

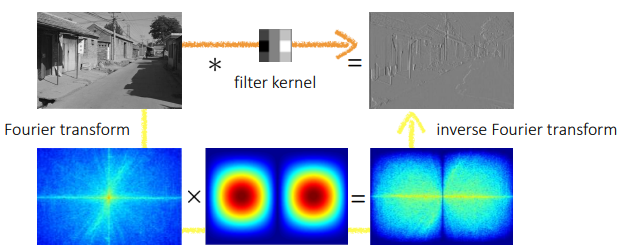
가우시안 Blur

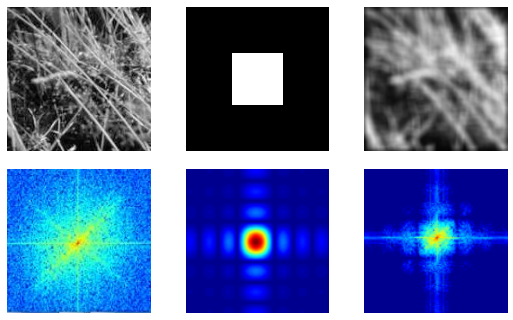
Box Blur

More filtering examples

Revisiting Sampling

The Nyquist-Shannon sampling theorem

minimum: 6Hz,
▶ 6Hz ↑ : aliasing X
▶ 6Hz ↓ : aliasing O