- 문제 (1026번) : 보물
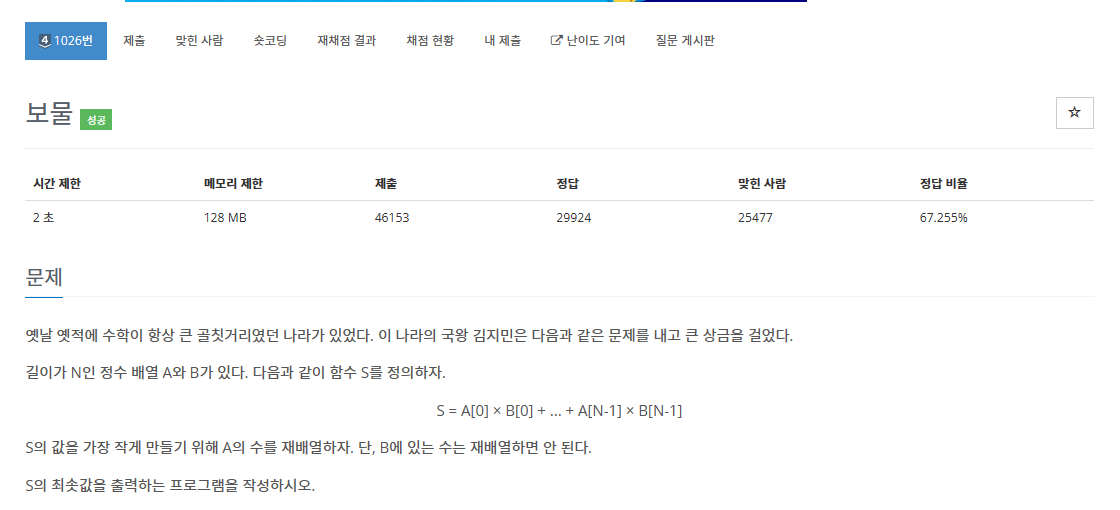
- 크기가 같은 배열 두개가 주어졌을 때 동일한 인덱스에 있는 값끼리 곱한 값을 더한 S의 최솟값 구하는 문제
∑ ( A[ i ] * B[ i ] ) 의 최솟값
- 입력 및 출력
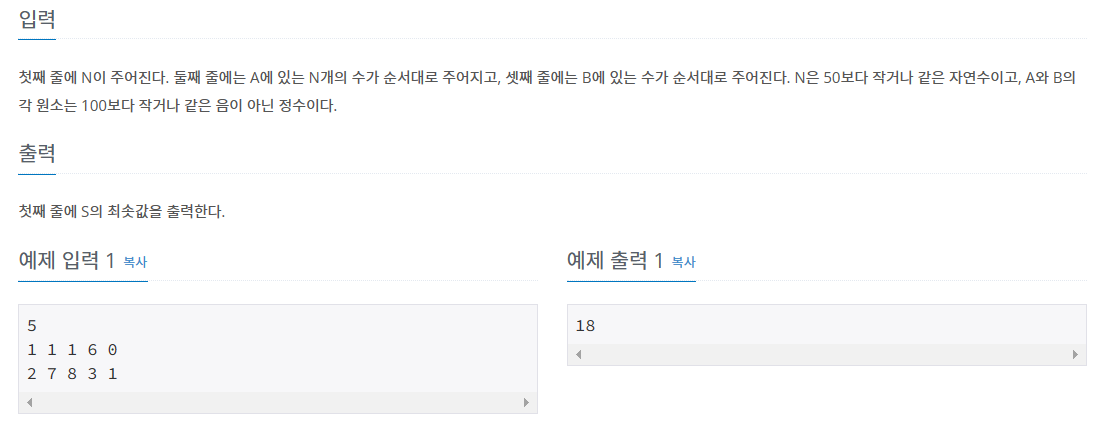
[ 입력 ]
- 첫째 줄에 배열의 크기 N 입력 ( 1 ≤ N ≤ 50 , 자연수 )
- 두번째 줄에 배열 A에 있는 N 개의 수 입력
- 세번째 줄에 배열 B에 있는 N 개의 수 입력
- 배열에 저장되어있는 각 원소는 100보다 작거나 같은 음이아닌 정수
[ 출력 ]
- 계산한 S의 최솟값 출력
- 문제 풀이
-
이 문제는 동일 인덱스에 존재하는 값끼리 곱한값을 더하는 문제다.
이것의 합이 제일 작으면 되므로, 동일 인덱스에 존재하는 값끼리 곱한값이 최소가 되면 되는 것이다. -
동일 인덱스에 존재하는 값의 곱이 최소가 되려면,
배열 A 중에서 가장 큰 값 x 배열 B 중에서 가장 작은 값
을 구해 더하면 된다.
-
위와 같이 해결하려면 배열 하나는 내림차순으로, 나머지 배열 하나는 오름차순으로 정렬해 동일 인덱스에 존재하는 값들을 곱한 후 더하면 해결된다.
ex) A : 1 5 6 3 2 || B : 6 0 1 1 2
- 배열 A는 오름차순으로 정렬 : 1 2 3 5 6
- 배열 B는 내림차순으로 정렬 : 6 2 1 1 0
- 각각의 수를 곱한 후 더한 값이 최소가 된다.
S = 6x1 + 2x2 + 3x1 + 5x1 + 6x0 = 18
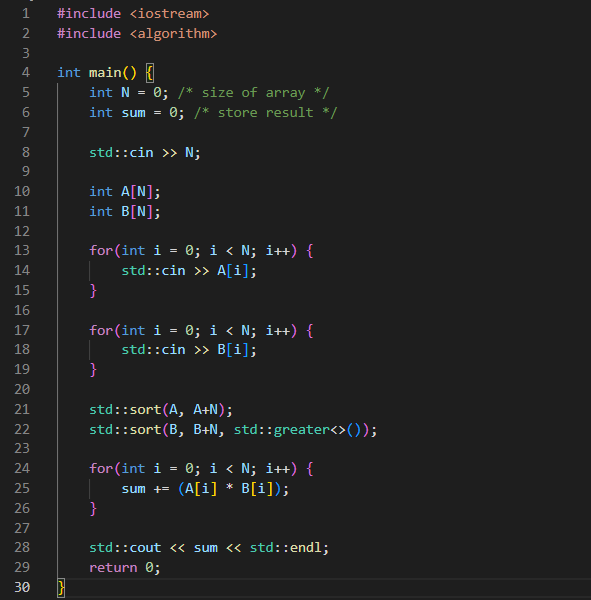
- 최종 코드