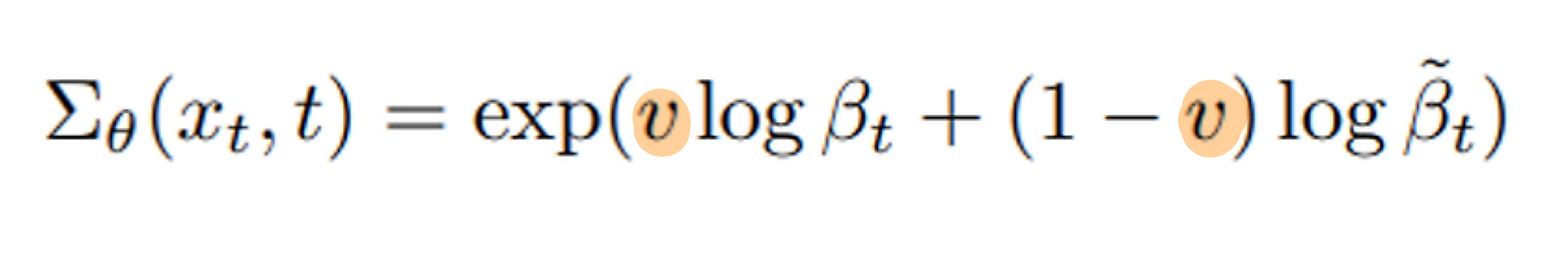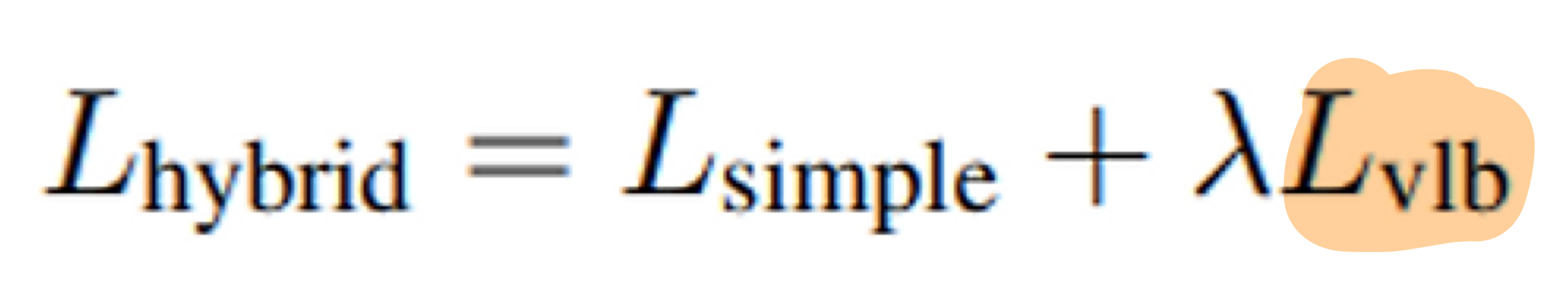- Improved-DDPM: Improved Denoising Diffusion Probabilistic Models
0. 들어가기 전에
- 저는 아래의 글들을 참고했습니다.
- 원 논문: https://arxiv.org/pdf/2102.09672
- github: https://github.com/openai/improved-diffusion
- DDPM에 대해 먼저 복습하자!:
0.1. 추가 공부 자료
- FID ? IS? : https://velog.io/@jk01019/FID-IS-그리고-DDPM
- mode coverage ? precision ? recall ? : https://velog.io/@jk01019/coverage-precision-recall
1. 뭐하는 논문?
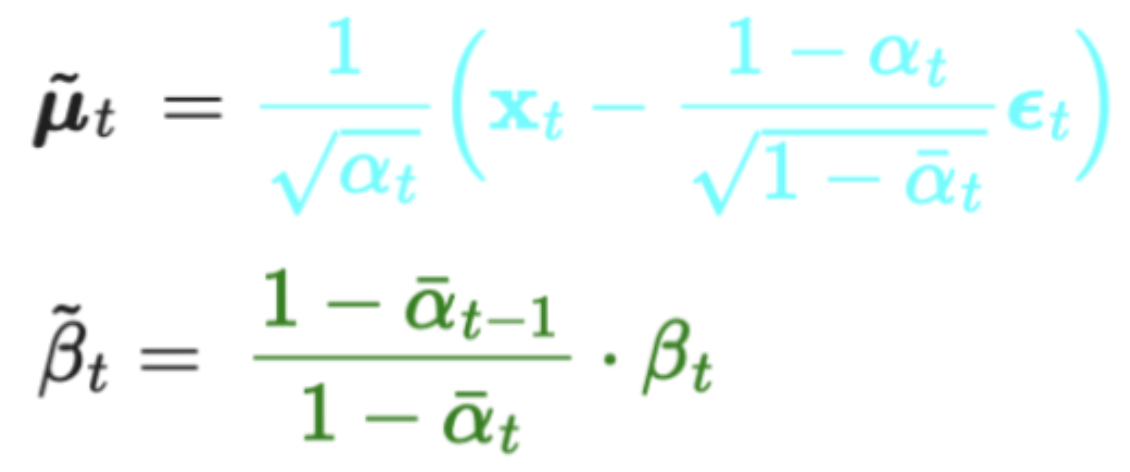
- DDPM에서 조금 개선해서, 높은 log-likelihood를 달성
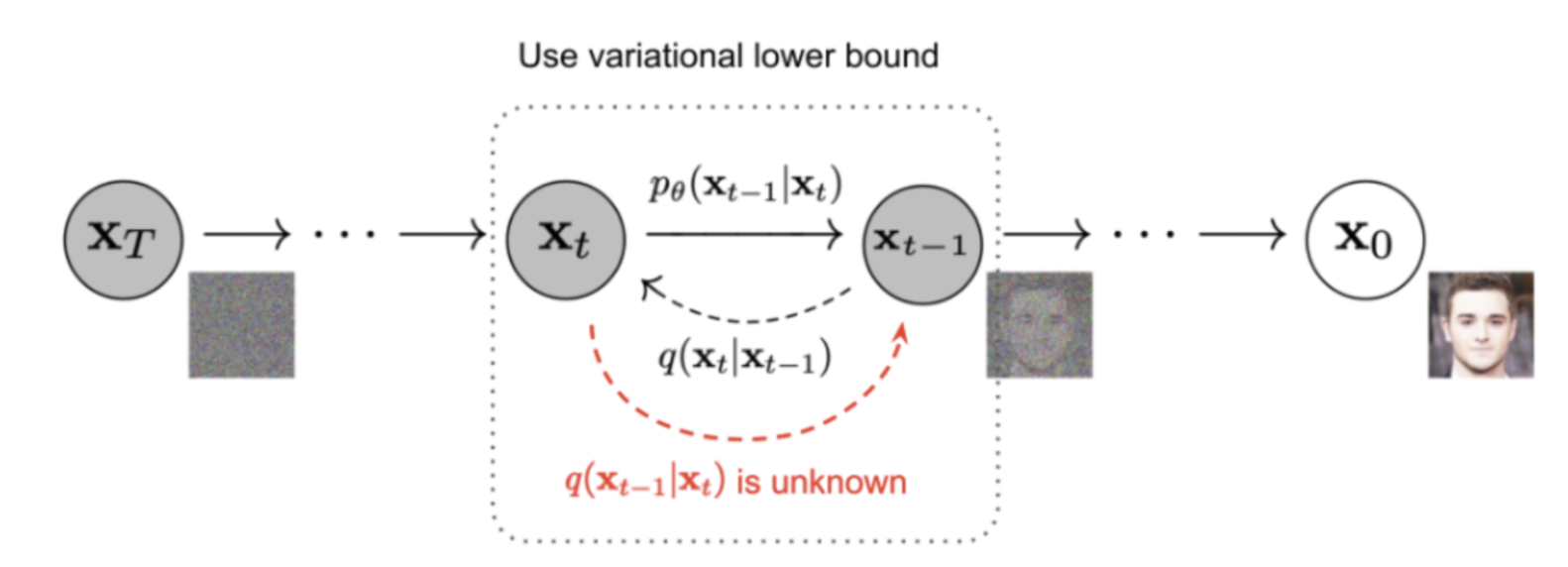
- reverse diffusion process에서,
- DDPM에서는
q(x_t-1|x_t)의 평균을 학습하기 위한ϵ_t만 학습했었다. - 분산까지 맞추도록 학습하면, log-likelihood가 더 높게 학습되더라!
- DDPM에서는
- 분산까지 맞추도록 학습(T step으로 hyperparameter 설정)하니, inference(sampling) 시점에서,
- 0 -> 1 -> 2 -> ... -> T step으로 순차적 sampling을 하지 않고
- 0 -> 3 -> 6 -> ... -> T step 처럼, 더 적은 step으로 sampling해도, 큰 퀄리티 차이 없이 sampling이 가능하다는 것을 확인!
- diffusion을 GAN과 정량적 비교 해보고 싶었다.
- GAN은 log-likelihood 기반 모델이 아니어서,
- diffusion에 precision-recall 매트릭을 도입하여 coverage를 측정해보았다.
- 그 결과,
- diffusion은 recall(coverage) 에 우수하고,
- GAN은 precision에 우수하더라.
- DDPM도 model size(학습 parameter 개수)와 연산량을 선형적으로 증사시킬수록, likelihood가 선형적으로 증가하는 것을 확인했다!
- scalability가 좋더라!
2. VLB를 직접 loss function으로?
- DDPM ( https://velog.io/@jk01019/Diffusion-오렌지-노트-한국어-정리 ) 에서 배웠듯이, log likelihood를 극대화 하려면, VLB 를 최소화시켜야 합니다.
- DDPM이 FID/IS 메트릭에서는 좋은 성능을 기록했지만, log likelihood 학습 성능에서 VAE/GAN에 비해 아쉬웠습니다.
- log likelihood는 생성 모델이 데이터 분포의 mode를 학습하도록 돕습니다.
- log likelihood가 조금만 개선되어도, 샘플 퀄리티와 학습된 feature representation이 좋아진다는 연구가 존재
- 그래서 DDPM과 달리, VLB 자체를 loss function으로 쓰면 어떨까 테스트해보았습니다.
- VLB는 Log likelihood의 lower bound 이므로
2.1. 문제점
- 결과는 학습 성능이 별로였습니다. 그 이유는, VLB 학습 시 많은 gradient noise가 생겼기 때문인데요.
- 이는, 학습시 hyperparmeter T step에서, uniform sampling을 하면서 학습시켰기 때문입니다. 이게 왜 문제가 되냐면
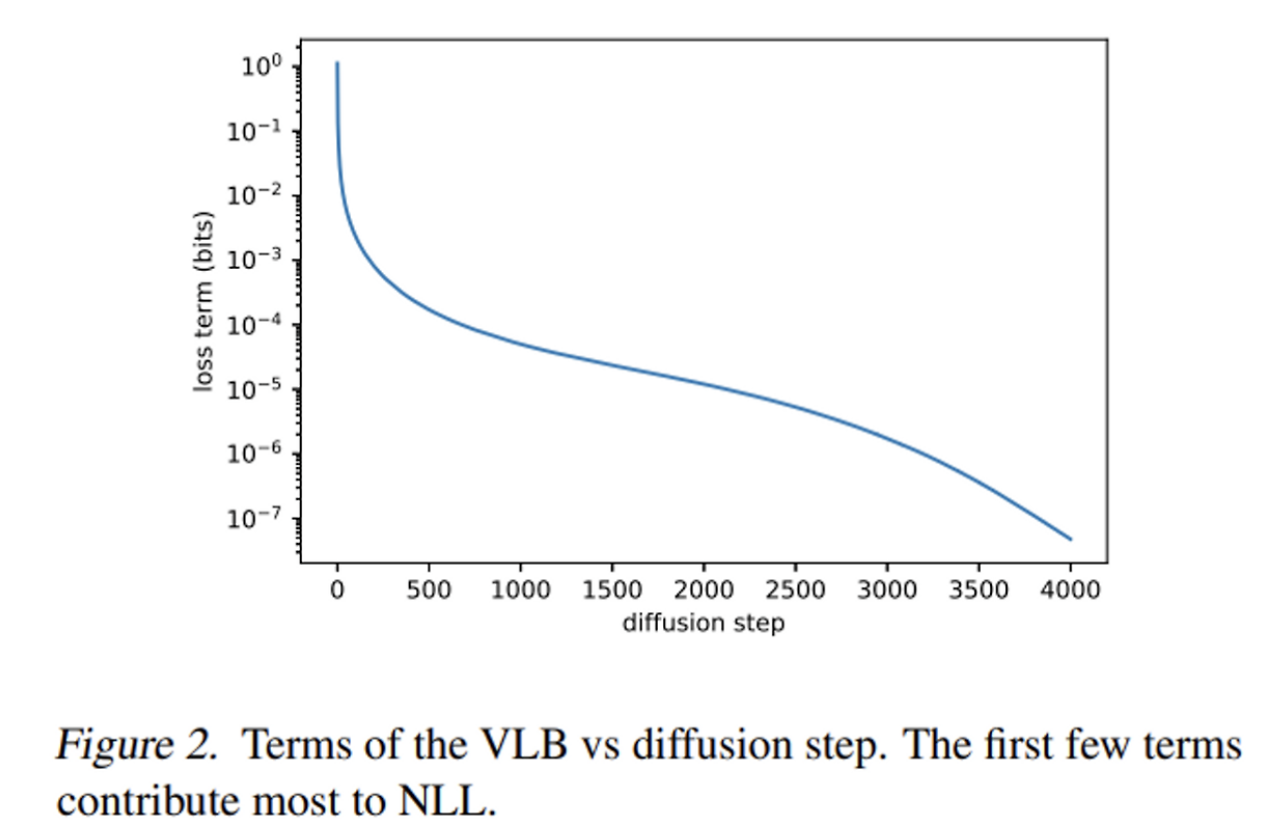
- TODO: 아래 내용 확실하지 않음
- 위 그림은 학습 다 시킨 모델을 inference 시, 각 step에서 발생한 loss를 그래프로 나타낸 것입니다.
- 그림을 보면, 각 step별로, loss의 발생 크기 정도가 다릅니다.
- TODO: 위 그래프가 inference시 그래프인지, training시 그래프인지 확인할 필요 있음
- 허나, 우리는 학습 시 t를 uniform sampling 했기 때문에, VLB 학습 시 많은 gradient noise가 발생했던 것입니다.
2.2. 해결책
- 학습 시 t를 uniform sampling 하는 대신, importance sampling을 수행합니다.
- 어떻게 하는거냐면,
- T hyperparamter을 설정한 후에(예: 100),
- 먼저, 0, 1, ..., 100이 모두 최소 10번 이상 sampling 될 떄까지, uniform sampling하면서 학습시킵니다.
- 위 과정이 끝나면, 이제 그림 2와 같이 t 별 loss 분포를 알 수 있습니다.
- 이제부터, 위 그림2를 확률분포처럼 사용해서 t를 sampling하면서 학습합니다.
- 대신, 확률이 큰 t의 loss가 자주선택될테니, p_t로 나누어 작게 반영합니다.
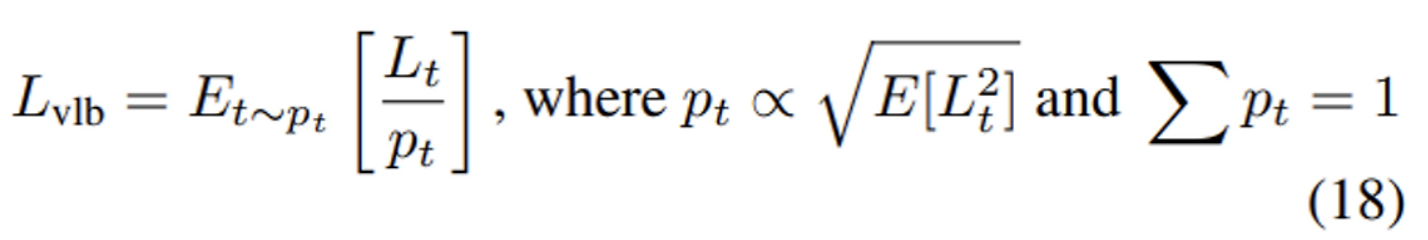
- 이렇게 하니, 아래와 같은 그래프가 나왔다!
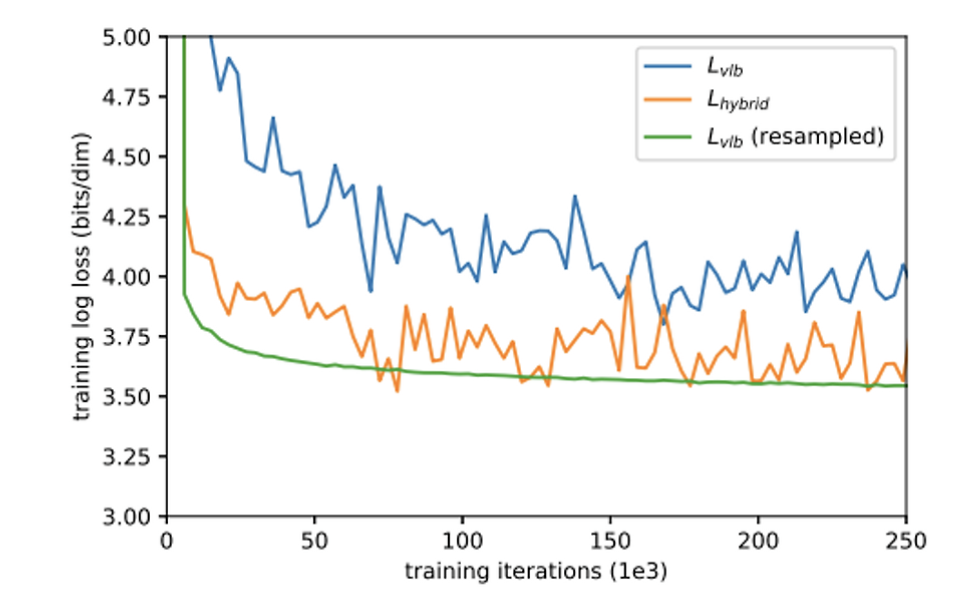
- 위 그래프를 해석해보면
- VLB loss는 gradient noise가 심해 학습이 불안정하나,
- resampled VLB loss는 안정적으로 학습되어 loss가 가장 많이 줄어듭니다.
- 다만, 이 importance sampling 방식은, L_hybrid(아래에서 서술할것임) 에는 먹히지 않는 방법이었다.
2.3. 결론
- DDPM이 log-likelihood 측면에서 성능이 아쉬웠고, 이를 극복하기 위해 log-likelihood를 direct하게 극대화시킬수 있는 VLB loss를 도입하였다.
- VLB loss의 단점인 gradient noise로 인한 학습 성능 저하를 극복하기 위해, importance sampling을 적용하였고, log likelihood를 극대화할 수 있었다.!
2.4. VLB loss의 side effect?
- 실험을 돌려보니, vlb loss를 이용하면 log-likelihood는 더욱 좋아지지만, FID를 희생하는 결과를 보여주었다.
- 기존 DDPM과 비슷한 FID 성능을 유지하면서도, log-likelihood 만 성능을 높일 수 있는 방법은 없을까?
3. 기존 DDPM은 왜 log-likelihood가 낮을까? 개선하고 싶다!
3.1. 원인 분석
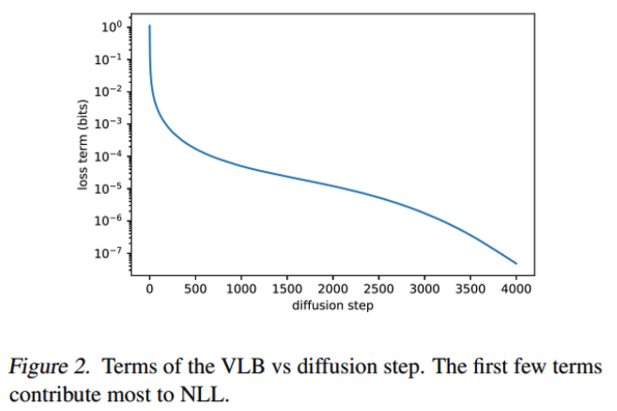
- TODO: 아래 내용 확실하지 않음
- 위 그림은 학습 다 시킨 모델을 inference 시, 각 step에서 발생한 loss를 그래프로 나타낸 것입니다.
- 그림을 보면, 각 step별로, loss의 발생 크기 정도가 다릅니다.
- TODO: 위 그래프가 inference시 그래프인지, training시 그래프인지 확인할 필요 있음
- 위 그림을 보면, VLB loss는 초기 phase(noise가 엄청 많은 시점)에서 크게 나타난다는 것을 볼 수 있습니다.
- 초기 phase의 Loss를 많이 줄일 수 있다면, 우리는 log-likelihood를 극대화할 수 있을 것입니다.
- 그렇다면 왜 초기 phase의 loss는 클까요?
원인 해결 1: P_theta(x_t-1|x_t) 의 분산을 학습시키기
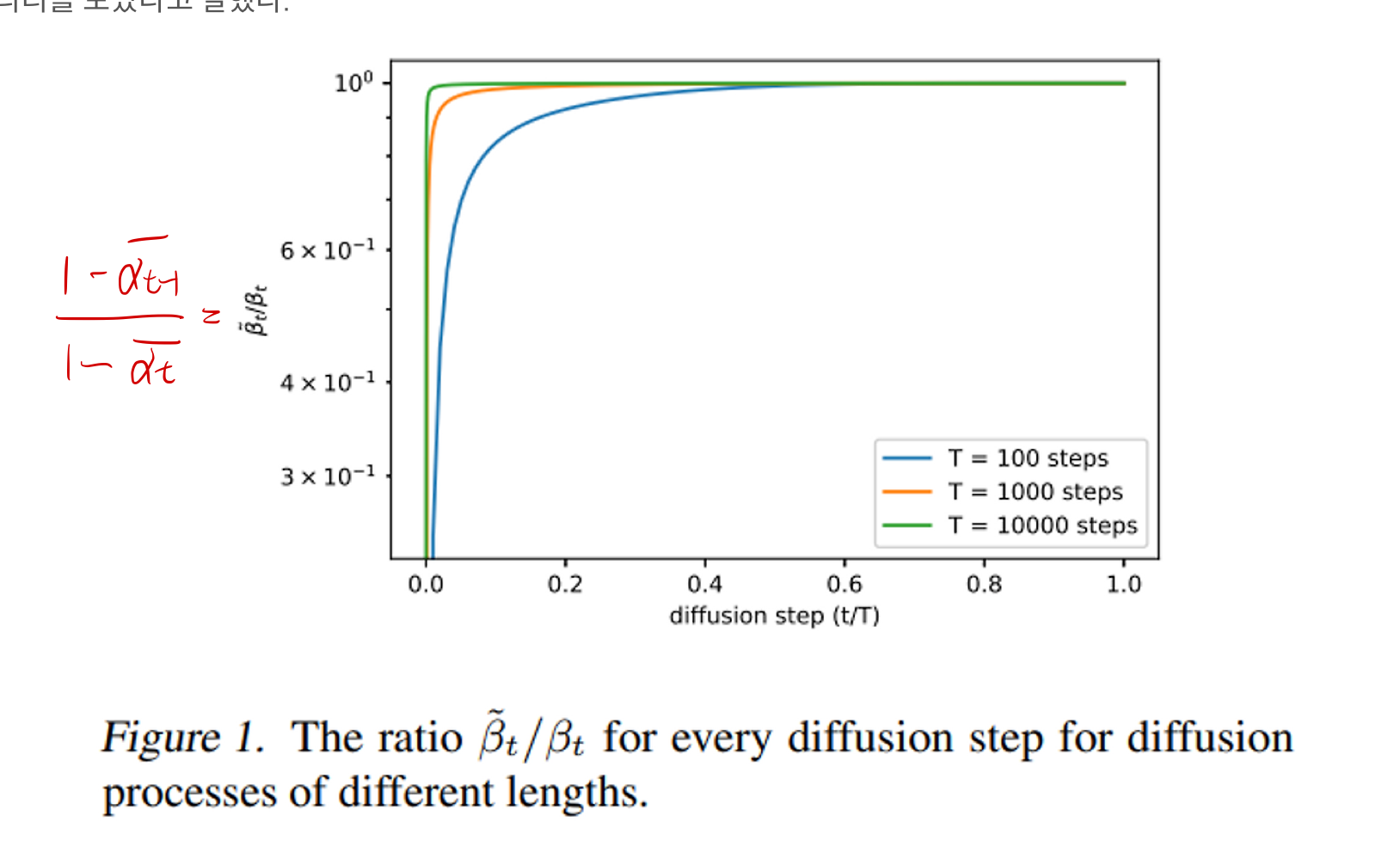
- 위 그림은
- DDPM을 다른 T hyperparameter로 학습 시킨 뒤,
- inference(sampling)을 각각하면서
~β_t / β_t가 어떻게 변화하는지 그린 그래프
- inference(sampling)을 각각하면서
- 참고로 ~β_t은
P_theta(x_t-1|x_t)normal distribution의 variance로써, DDPM에서 증명했습니다.
- DDPM을 다른 T hyperparameter로 학습 시킨 뒤,
- 우리는 DDPM에서, 분산을 따로 학습시키기 않았었습니다.
- reverse process에서 우리는 ϵ_t 만을 출력하도록 학습했고, 이는
P_theta(x_t-1|x_t)의 평균을 학습시키는 과정이었습니다. 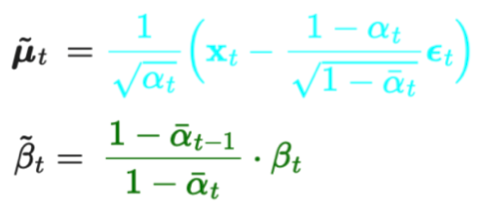
- reverse process에서 우리는 ϵ_t 만을 출력하도록 학습했고, 이는
- 분산은 학습시키지 않고, 아래와 같이 고정시켰습니다.
- Σₜ(xₜ, t) = σₜ²I
- 여기서 σₜ는 학습되지 않고 σₜ= βₜ
- 위 그래프를 다시 보면,
- inference 초반 (sampling 시) 에는 βₜ가 ~β_t와 차이가 크다가, sampling이 진행될수록 차이가 줄어들어서 같아지게 됩니다.
- T hyperparamter가 클수록, 차이의 영향은 줄어들긴 합니다.
- 여기서 알 수 있는 점은,
- Figure 2를 보면 inference 초반 (sampling 시)에 VLB loss가 큰데,
- Figure 1을 보면, inference 초반 (sampling 시)에 variance estimation 성능이 떨어진다는 것을 볼 수 있습니다.
- 그러므로, 우리는
분산까지 학습시켜서 esimation하면 VLB loss, 즉 log-likelihood가 개선될까? 라는 생각을 가질 수 있습니다.
이유 1을 개선하기
- 자 이제 denoising process를 담당하는 deep learning network가 기존 ϵθ (즉, 평균) 만을 출력하는 것에서 업데이트 해서
- ϵθ (즉, 평균) 와 Σₜ(xₜ, t) 까지 학습하도록 해봅시다.
- 다만, Σₜ(xₜ, t)는 유효한 범위가 매우 작아서, direct 학습은 어렵다고 합니다.
- 이를 해결하기 위해 모델의 output을
v를 출력하도록 학습합니다.v는 아래와 같습니다. - 모델의 output에
v를 추가했으니, 이를 학습되게 하기 위해서 loss function도 수정해봅시다. - 기존 DDPM의 loss는 아래와 같았습니다.
- L_simple에는, 분산을 학습시키는 term이 없어서 추가해줘야 합니다.
- Improved DDPM에서는 아래와 같이 변경하였습니다.
- vlb의 μ 에서는 stop gradient를 사용하여,
- simple loss가 μ 에 영향을 끼치는 메인 loss,
- vlb loss가 분산을 담당하도록 유도하였다.
- 실험을 통해 λ 가 0.001일 때 vlb loss가 simple loss를 overwhelming하지 않는다는 것을 찾았다.
- 결론
- 이렇게
P_theta(x_t-1|x_t)의 분산까지 학습시키므로써, log-likelihood가 개선되는지 확인해보자!
- 이렇게
원인 해결 2: Noise schedule의 개선
- 앞선 그림 2를 보면, VLB loss는 초기 phase(noise가 엄청 많은 시점)에서 크게 나타난다는 것을 볼 수 있습니다.
- 초기 phase의 Loss를 많이 줄일 수 있다면, 우리는 log-likelihood를 극대화할 수 있을 것입니다.
- 그렇다면 왜 초기 phase의 loss는 클까요?
- 우리는 DDPM에서 Bt를 linear schedule로 설정하였습니다.

- 그 결과, 위 그림 3의 첫번째 row를 보면, 선형 Bt를 준 경우, 중간 단계에서부터 벌써 almost noisy한 것을 볼 수 있습니다.
- 이게 왜 문제가 될까요? DDPM을 학습 다 시킨 후, inference(sampling)시,
- reverse process의 초기 부분을 몇 % skip하는지에 따라, 성능(FID)가 얼마나 안좋아지는지를 실험해보았습니다.
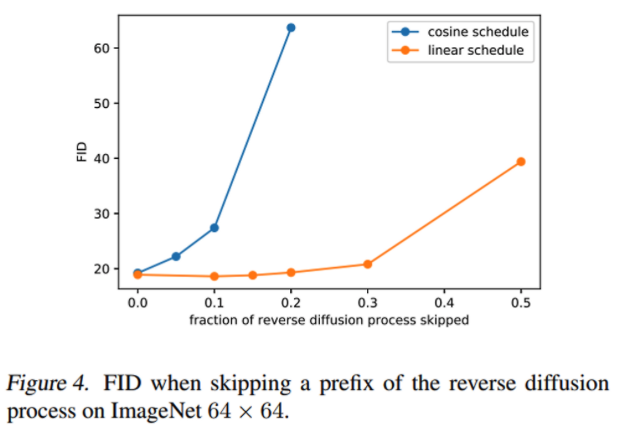
- 주황색 그래프를 보면, 초반 부분을 skip을 해도, reverse process가 생성하는 이미지의 퀄리티는 별 차이가 없었습니다.
- 즉, 다른 말로 하면, reverse process의 초반부 (forward process의 후반부)의 학습은 별 의미가 없었다는 뜻입니다.
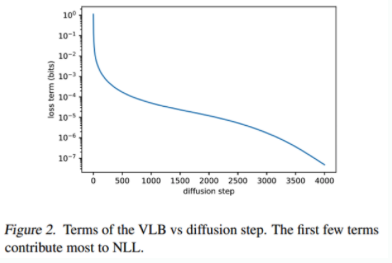
- 하지만 Figure 2를 보면, 학습 다 시킨 DDPM을 sampling 했을 때, 초반부의 VLB loss가 가장 크다고 했죠?
- 즉, 의미 없는 학습 과정이 있었기에, VLB loss(즉 negative log likelihood loss)가 크게 나온 겁니다.
- 이를 개선하기 위해 여러 실험을 진행했습니다.
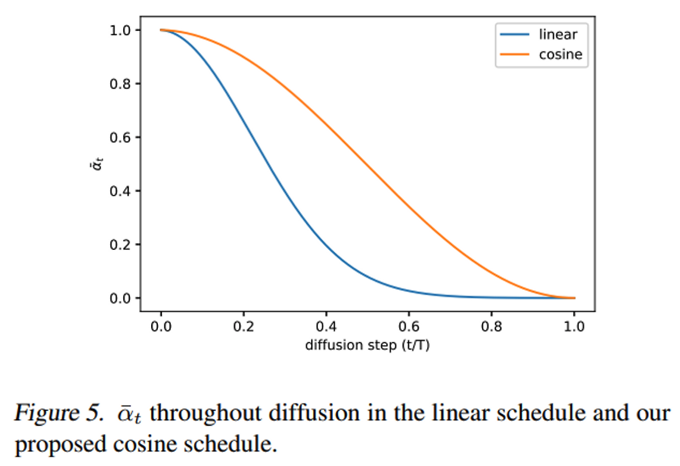
- 스케줄링 함수의 선택은 임의적일 수 있지만,
알파 헷은 아래의 규칙을 따르는게 좋다고 합니다. (아래 그래프 세로축 처럼)- 훈련 과정 중간에 거의 선형적인 감소를 제공하고
- t=0 및 t=T 근처에서는 미묘한 변화를 제공해야 합니다.
- 대표적인 예가 코사인 기반 분산 스케줄을 사용하는 것입니다.
- input (normalized) image 의 값 분포가 -1 ~ 1 사이라는 점에서, variance(Bt)는 상대적으로 작다고 할 수 있습니다.
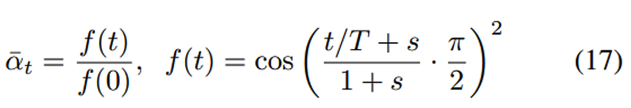
3.2. 개선점 2개로 얼마나 log-likelihood가 좋아졌을까?
- 후보군 1: cosine schedule + hybrid loss(분산도 학습)
- DDPM과 비교해서
- FID를 유지
- log-likelihood 개선
- DDPM과 비교해서
- 후보군 2: VLB loss only + importance sampling
- DDPM과 비교해서
- FID를 유지
- log-likelihood 가장 많이 개선
- DDPM과 비교해서
- 저자는
후보군1이 더 좋은 선택지라고 주장한다!
4. Sampling 속도 높이기
- hybrid loss(분산도 학습)을 적용하면, 우리가 학습때 hyperparamter T로 학습했다고 할지라도,
- inference(sampling)시
- 0, 1,2, ..., T 로 샘플링하지 않고
- subsequence인 S를 사용하여 샘플링 해도 (일정한 stride로 timestep을 줄이는 방식임)
- 고품질의 결과를 생성할 수 있다는 것을 보였다.
- inference(sampling)시
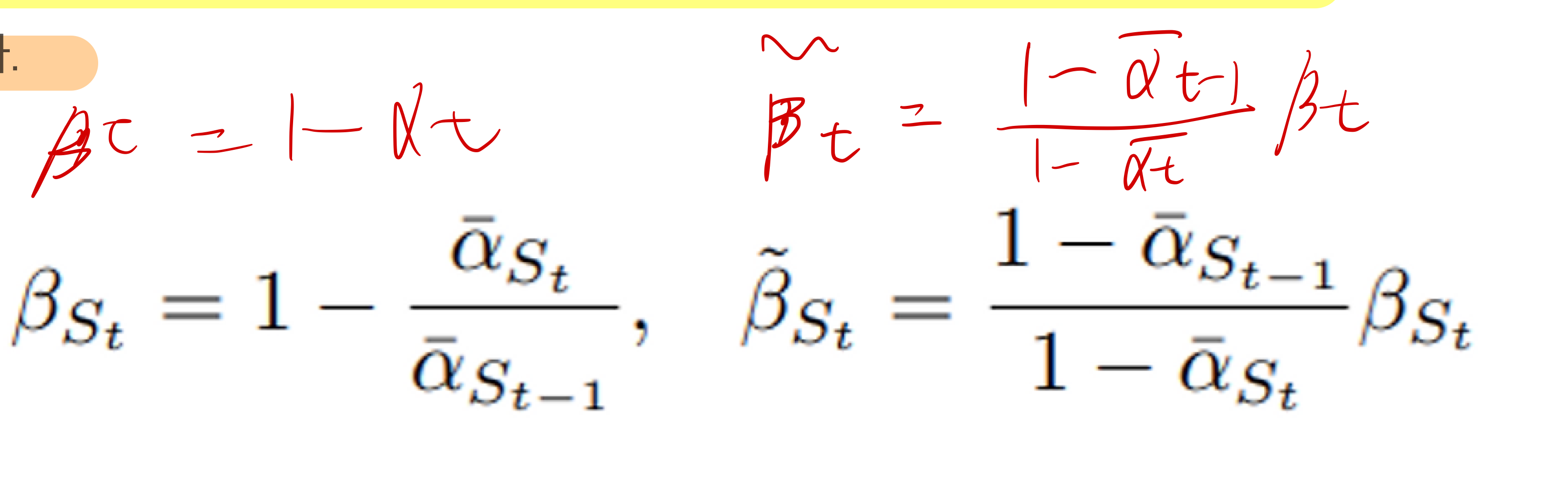
- 위와 같이 새로 sampling variance가 정의됨
- TODO: 위 수식 완전히 이해 필요
- sigma가 고정된 Lsimple 모델은 샘플링 timestep이 줄어듬에 따라 성능에 큰 타격을 받았지만,
- sigma를 학습하며 Lhybrid 를 사용하는 모델은 좋은 샘플 퀄리티를 유지하였다.
- 학습이 완료된 모델에서 제시한 세팅(learned sigmas, hybrid loss)는 학습에 사용한 4000 steps의 1/40인 100 step에서도 좋은 성능을 보였다.
- DDIM과 비교해 보면
- DDIM은 50보다 적은 steps에서는 더 좋은 샘플 퀄리티를 보였지만
- 더 많은 steps을 사용하면 본 논문에서 제시한 방법이 더 좋은 샘플 퀄리티틀 보였다.
- 일정한 stride로 timestep을 줄이는 해당 논문의 방식을 DDIM에 적용해 보았는데
- 성능이 크게 하락하여 DDIM 논문에서 제시한 본래 방식을 사용하였다.
- 반대로 DDIM의 quadratic striding 방식을 본 논문의 방식에 사용해 보았는데
- cosine schedule과 quadratic striding의 조합은 샘플 퀄리티를 저하시켰다.
5. GAN과의 비교
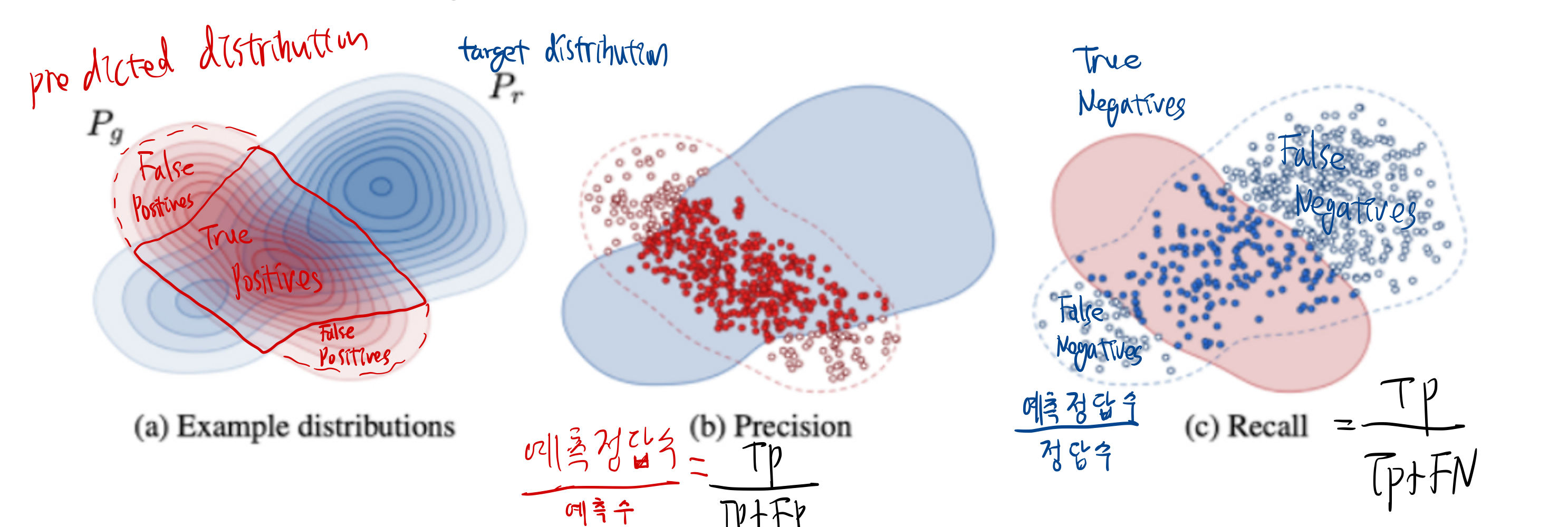
- likelihood가 mode-coverage를 유추할 수 있는 좋은 metric이지만 likelihood 기반 모델이 아닌 GAN에서는 이를 구할 수 없다.
- 대신 precision과 recall을 사용하여 BigGAN-deep과의 성능을 비교하였다.
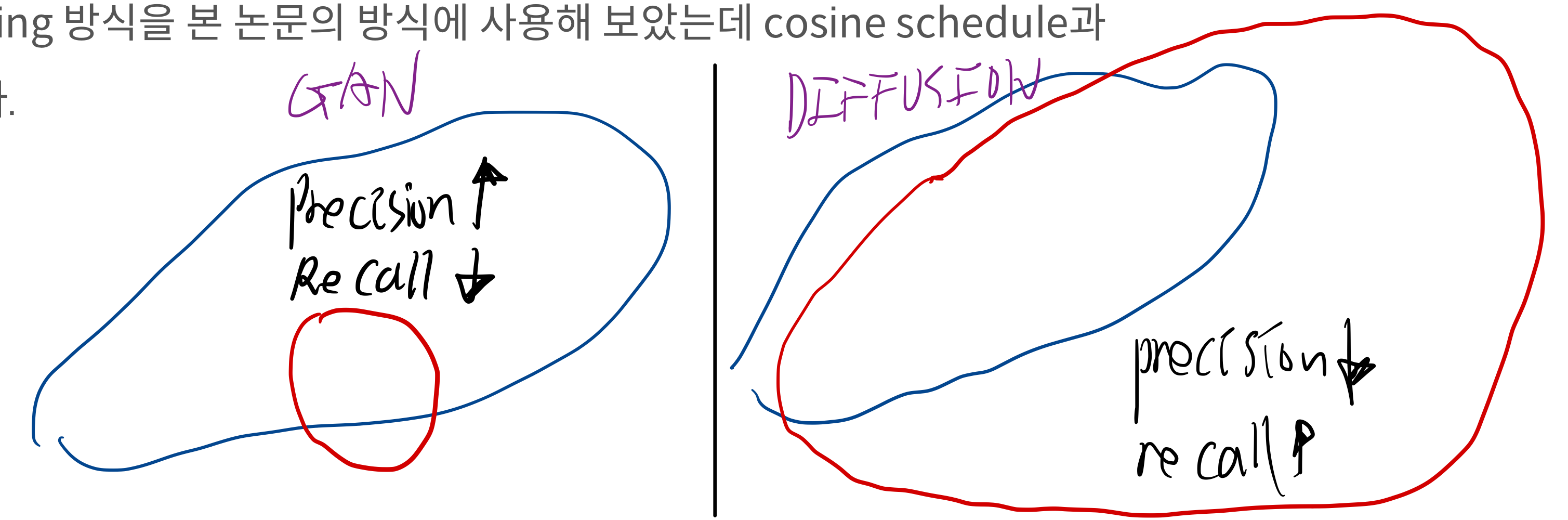
- GAN
- 높은 Precision, 낮은 Recall, 낮은 Coverage
- Diffusion
- 높은 Recall, 높은 Coverage를 보일 수 있지만, Precision은 GAN보다 낮을 수 있음
- 그림으로 비교: GAN VS Diffusion
6. DDPM의 scalability 입증
- DDPM은 model size가 커짐에 따라, 연산량이 클 떄 성은이 더 좋아짐 (scaling에 따른 성능 개선이 에측 가능)