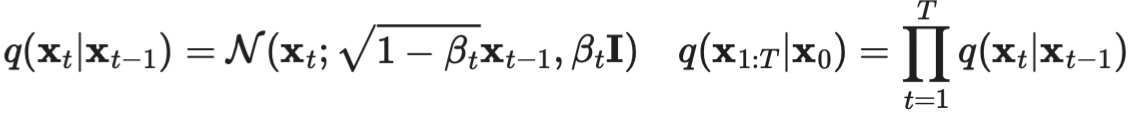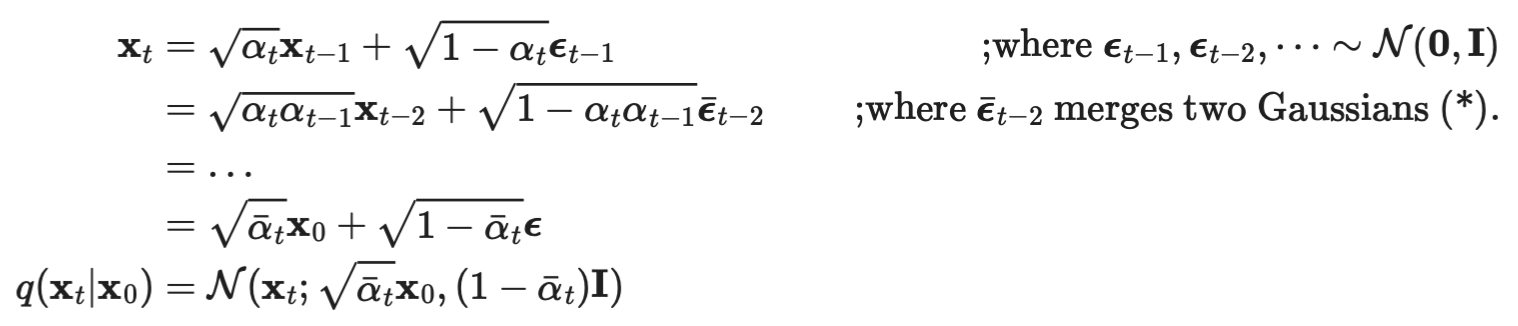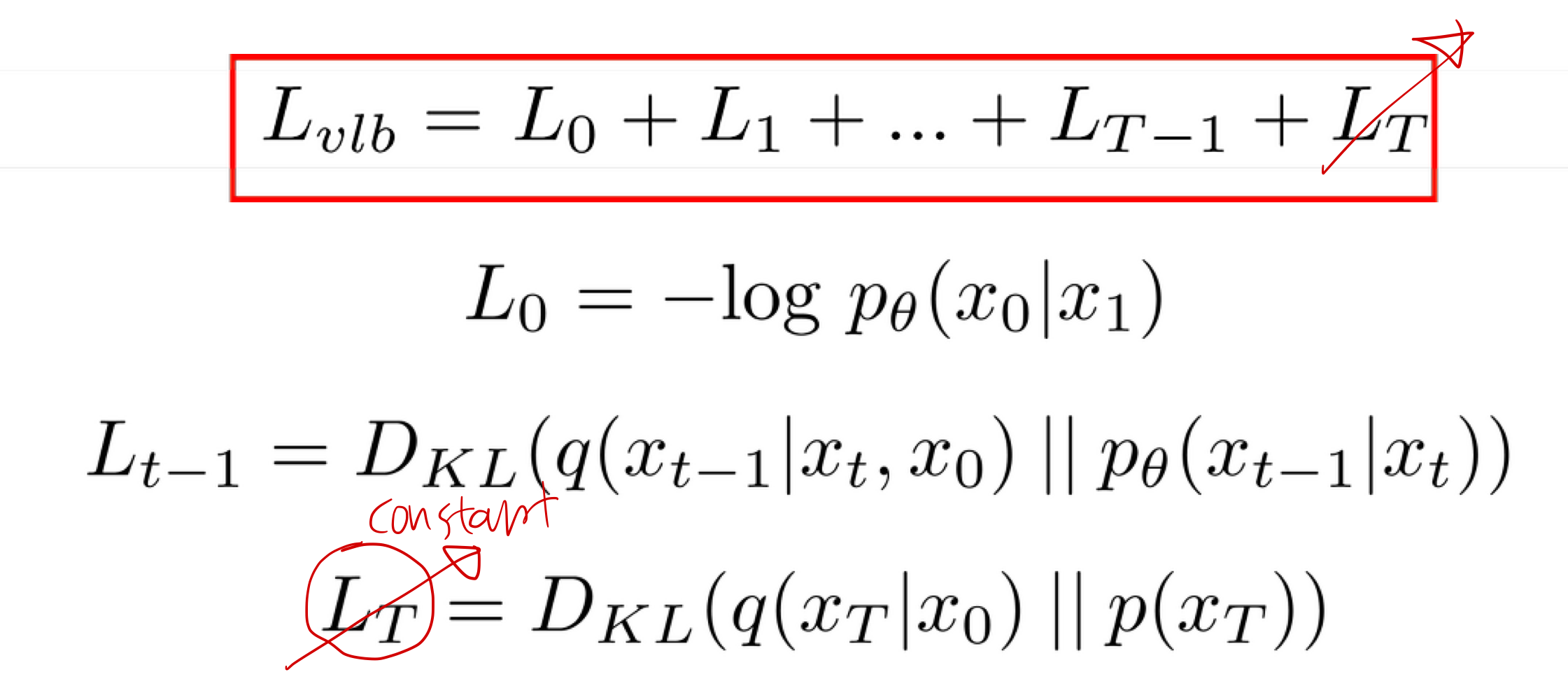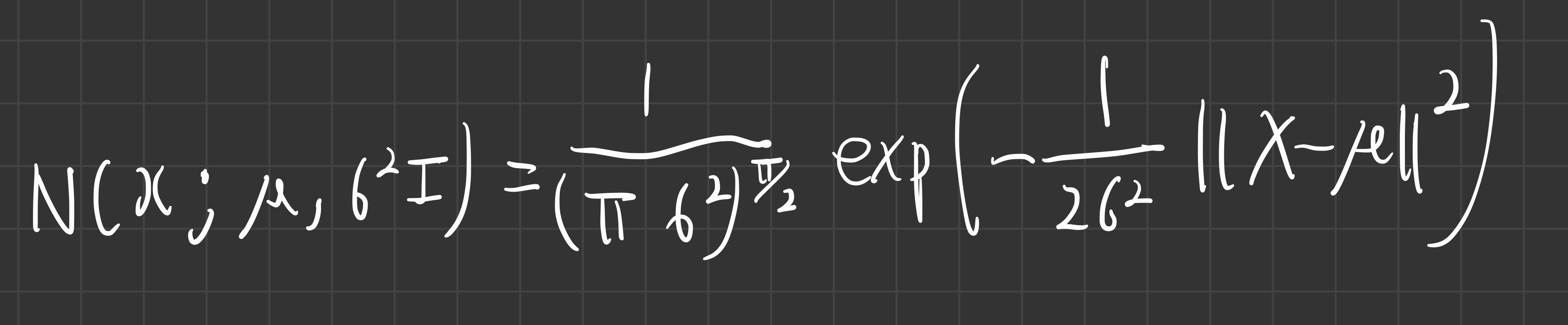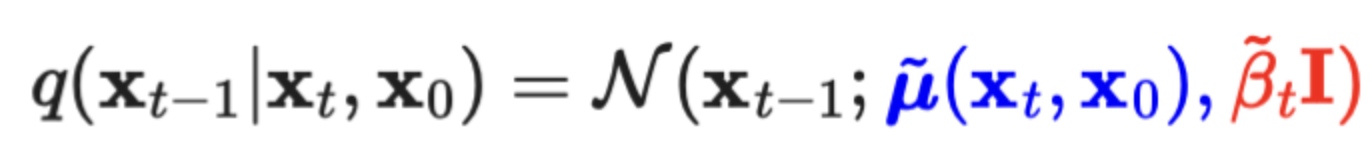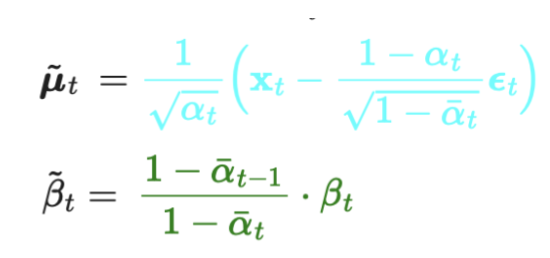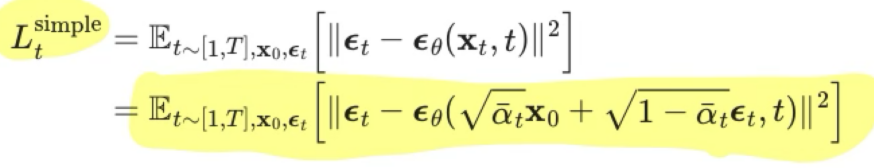들어가기 전에
- https://lilianweng.github.io/posts/2021-07-11-diffusion-models/ 을 한국어로 각색해 보았습니다.
- 감사합니다!
- 다음 링크를 통해 좀 더 쉽게 개념적으로 이해를 마치시고 ( https://velog.io/@jk01019/Diffusion-개념잡기-core), 그 후 이 글을 읽는 것을 권장합니다.
Why diffusion?
- VAE와 다르게,
- Diffusion 모델은
학습 과정이 사전에 정의된 특정한 방법을 따릅니다.- "노이즈 추가"와 "노이즈 제거"라는 일련의 과정을 기반으로 학습이 이루어지며,
- 이 절차는 모델마다 크게 변하지 않습니다.
- Diffusion 모델에서 latent variable은, high dimensionality ( 원본 데이터의 차원과 동일)
- Diffusion 모델은
디퓨전 모델이 뭔데?
- DDPM (Denoising Diffusion Probabilistic Model) 과 같은 논문들이 duffsion-based 생성 모델을 제안
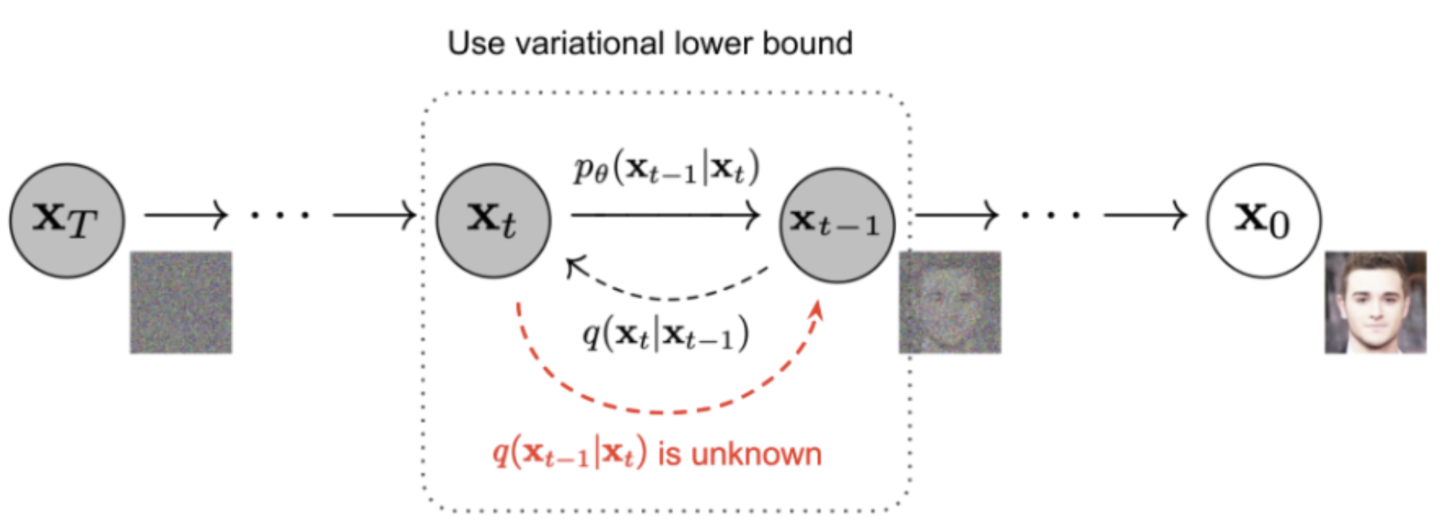
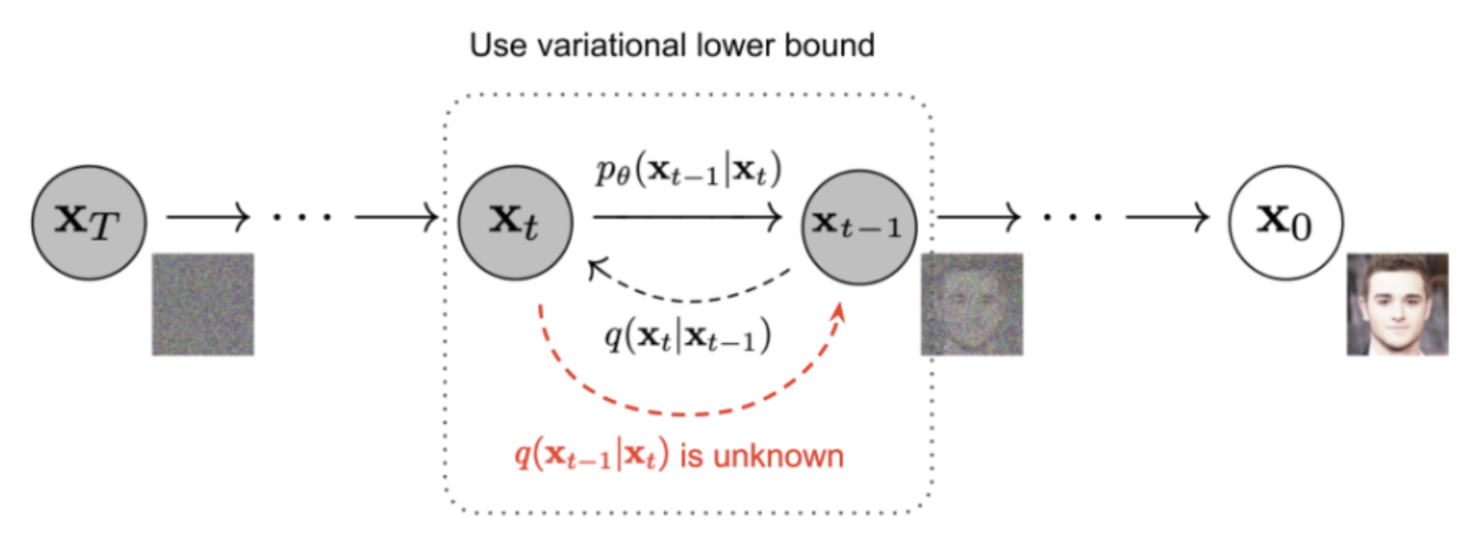
Forward Diffusion Process
Reverse Diffusion Process
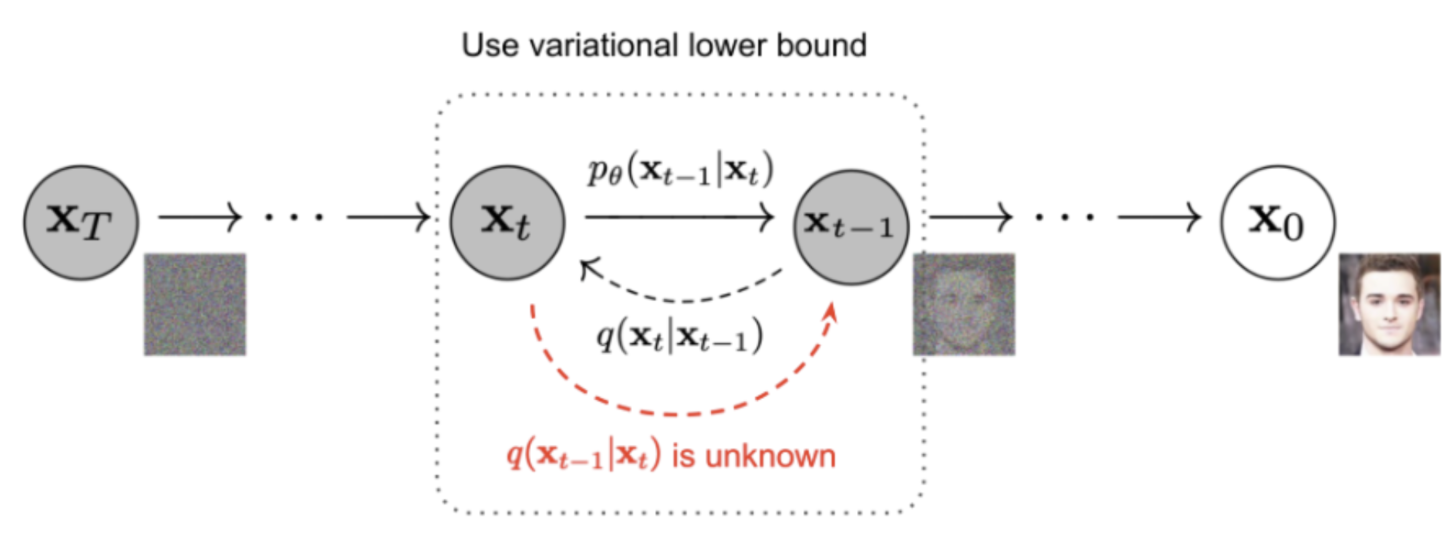
- 위 그림의 빨간색 글씨 q(x_t-1|x_t)를 알 수 있다면, 우리는 순수한 Gaussian noise input으로부터 true sample을 재생성할 수 있습니다.
- 하지만,
q(x_t-1|x_t)을 알려면, 전체 데이터셋이 필요하기 떄문에, 알 수 없습니다.- 우리는 대신, P_theta(x_t-1|x_t) 를 모델이 학습하는 방법을 통해, reverse diffusion process가 동작하게 합니다.
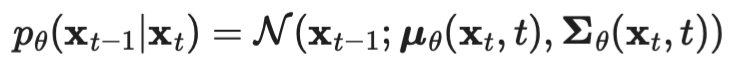
- 위와 같이 reverse process를 조건부 가우시안으로 설정할 수 이유는
- diffusion이 매우 작은 양의 gaussian noise로 구성된다는 전제 때문이다.
- βₜ가 매우 작다는 가정
개념적 Objective(Loss) Function
수학적 증명 전, loss fuction 개념적으로 이해하기
- 수식 증명/유도를 하기전에 결론부터 말하자면 Objective(Loss) Function은 아래와 같고, 이를 최소화하는게 목표이다.
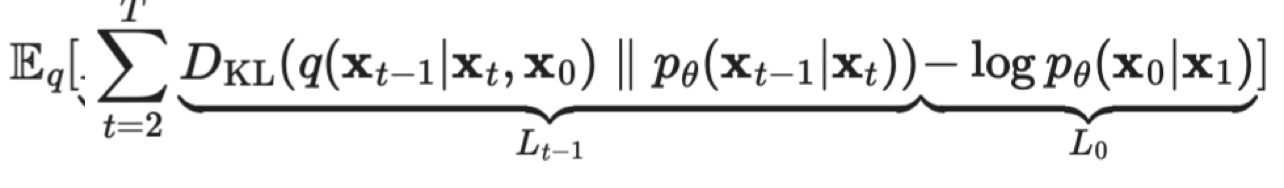
- 직관적으로도 이해하기 쉬운데, 우리는 q(x_t-1 | x_t)를 우회적으로 구하기 위해
P_theta(x_t-1|x_t)를 학습시키는게 목표이고, 그 이유에 대해서도 위에서 얘기했었다. - KL divergence라 함은, 두 확률분포의 유사도를 수학적으로 계산한 것이고, 값이 작아질수록 두 확률분포가 유사해진다는 뜻이므로, 합리적인 수식이다.
- 하지만, 우리는 수학적 증명을 통해,
q(x_t-1 | x_t)와P_theta(x_t-1|x_t)의 분포를 유사하게 학습시키는 것이, 왜 원래 input 이미지를 제대로 복원시키는 것과 동치인지 수학적으로 증명할 필요가 있다. 원래 input 이미지를 제대로 복원시키는 것=log[P_theta(X_0)] 를 극대화 한다.- 그려면 이제,
log[P_theta(X_0)] 를 극대화 한다.는 것이, 아래의 것과 동치임을 보이겠다.q(x_t-1 | x_t)와P_theta(x_t-1|x_t)의 분포를 유사하게 학습하는 것
수학적 증명하기
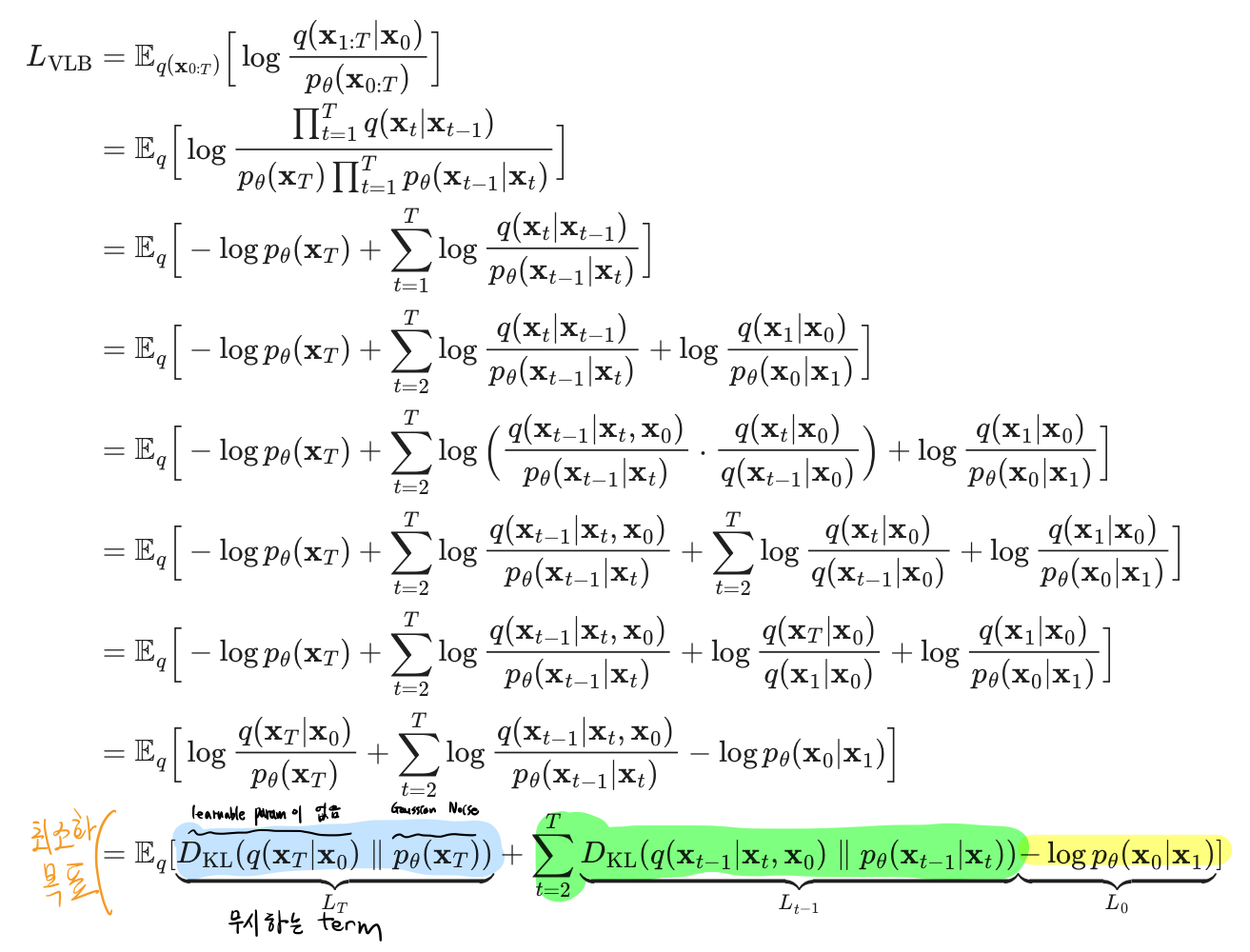
과정 1: Variational Lower Bound 유도하기
- 방법 1
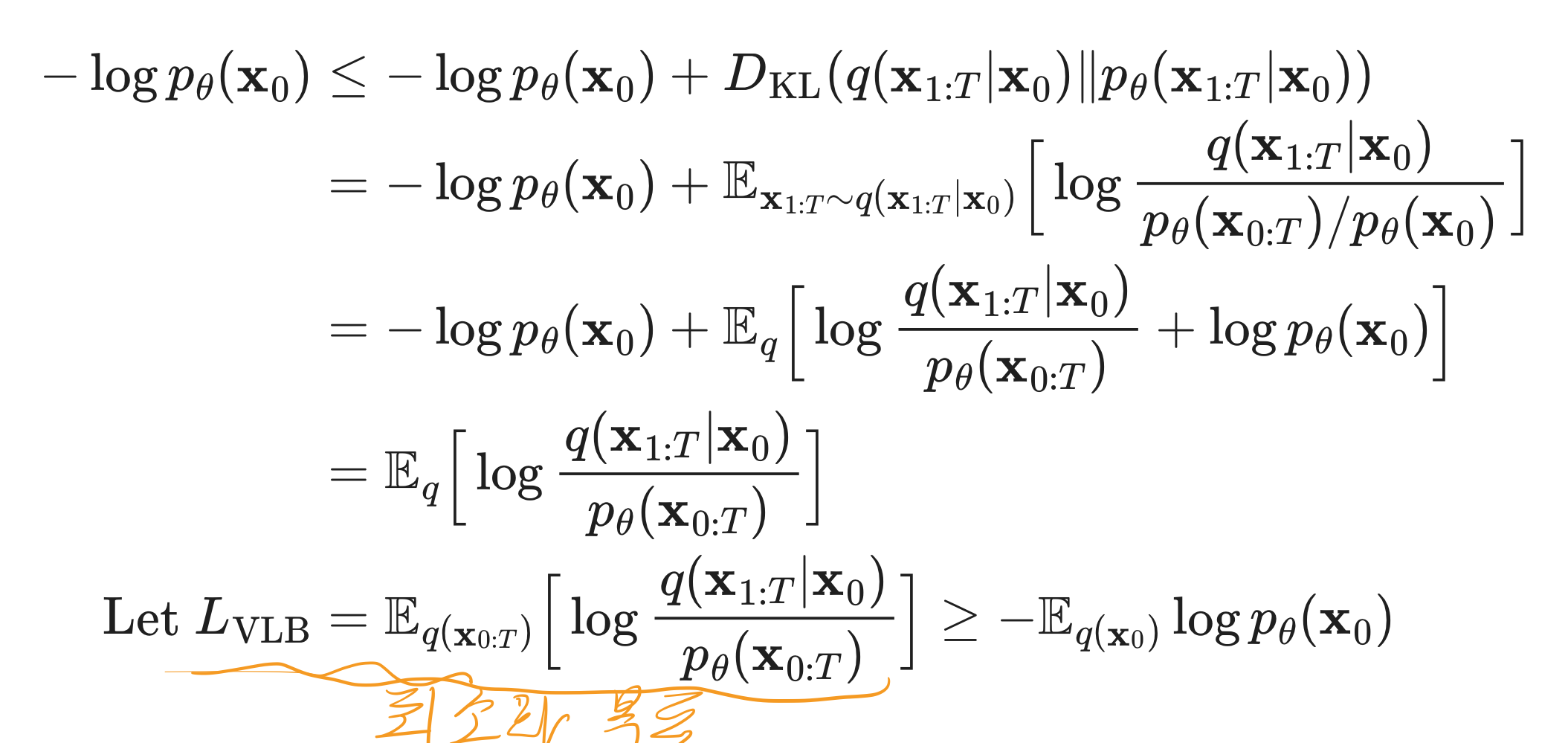
- 방법 2
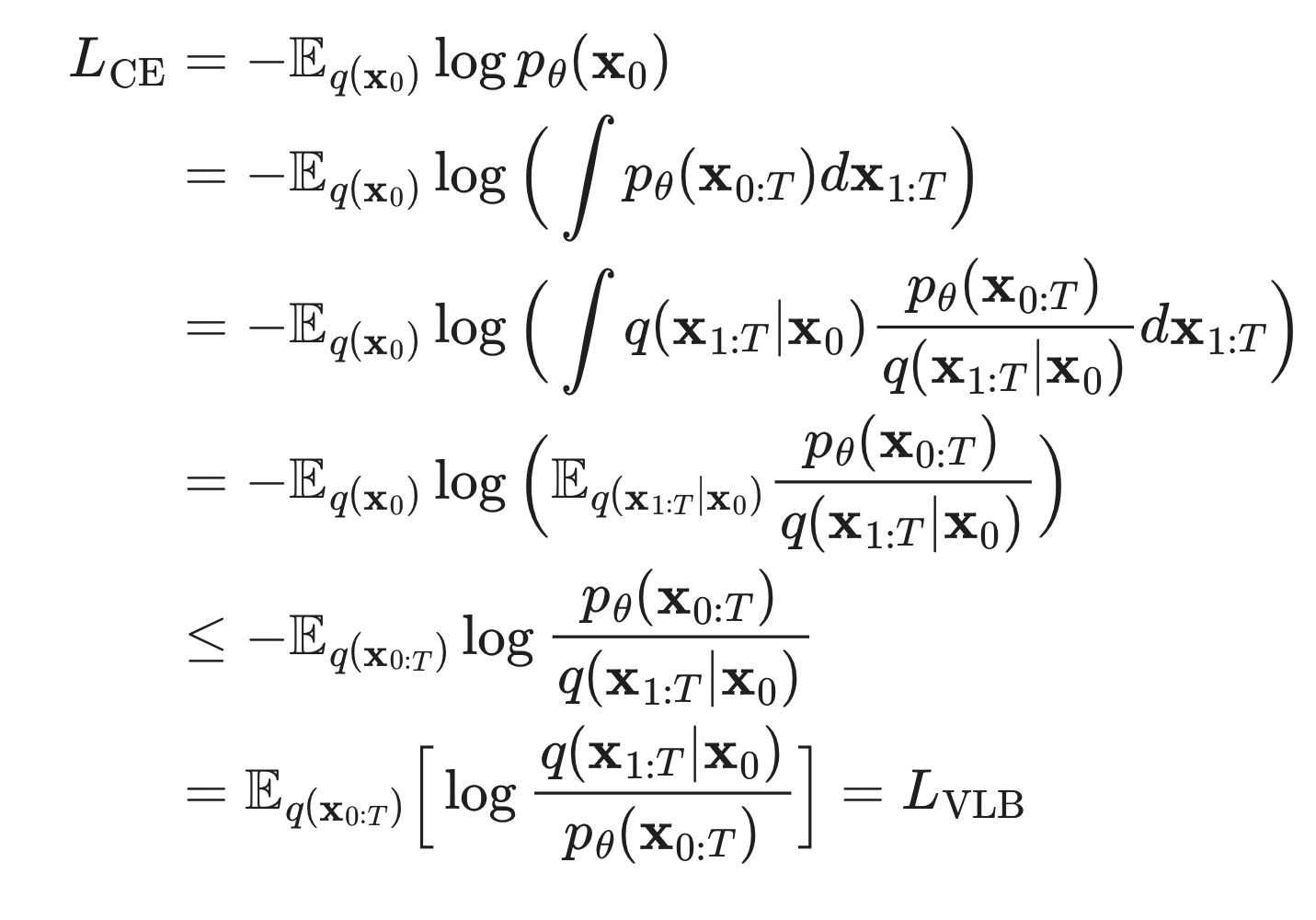
과정 2: Variational Lower Bound를 예쁘게 정리하기
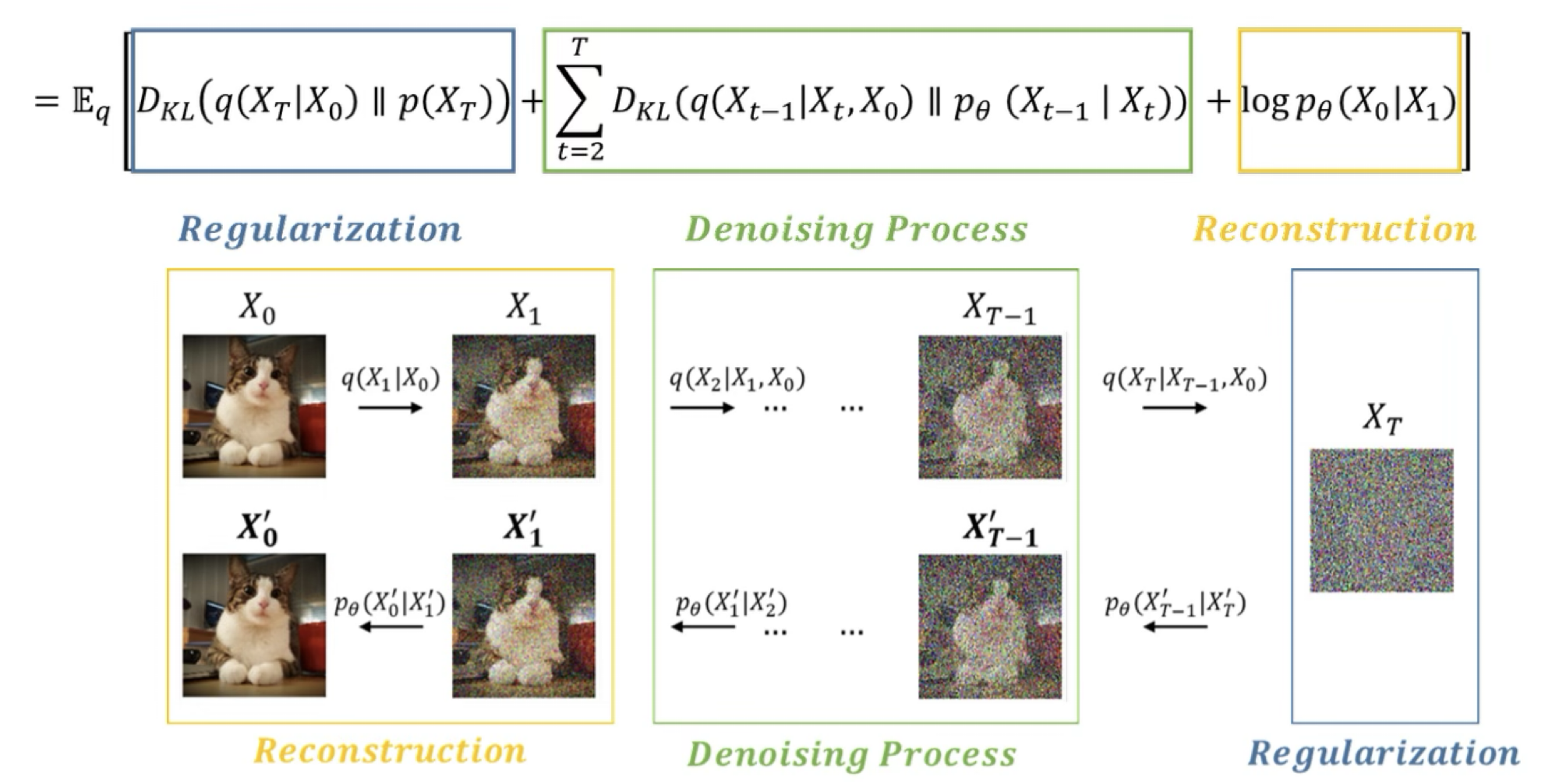
파란색: Regularization Term
- Regularization Term의 경우 굳이 존재하지 않더라도 되기 떄문에, 삭제함. (아래의 이유 떄문)
- Diffusion과정 자체가 gaussian의 가정에 있으며,
- T가 무한대로 갈 때 istropic gaussian이 된다는 가정을 두고 있음
- 즉, 굳이 가우시안을 따르도록 regularization을 해줄 필요가 없기에 이는 삭제 된다.
노란색: Reconstruction Term
- 실제로 Diffusion이라는 물리적 현상 자체가 인접한 small time step 에 대해서 small gaussian noise를 주입해주는 과정으로 진행되기에 x0와 x1에서의 차이는 거의 없다.
- 실제로 DDPM에서는 이에 대해서 ablation study또한 진행했고, reconstruction term은 너무 작기에 학습에 유의미한 영향을 끼치지 않기에 제거했다.
정리
학습 가능한 형태의 loss fuction ?
q(x_t-1 | x_t) gaussian의 평균과 분산 구하기

- 우리가 구하고 싶은 것: q(x_t-1|x_t)
- 우리는 x_0의 정보를 학습 시 알고 있고,
- x₀를 조건으로 할 때 -> reverse conditional probability가 계산 가능하다고 합니다.
- 그래서 q(x_t-1|x_t, x_0)을 구하는 것으로 목표를 바꿔봅시다.
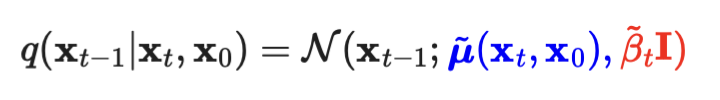
- 우리는 위 식에서, guassian 분포의 평균(파란색)과 분산(빨간색)을 구하는 것이 목표입니다.
- 자 이제, 수학적으로 평균(파란색)과 분산(빨간색)을 구해봅시다.
- 들어가기 전에: 다변수 정규분포의 확률 밀도 함수 수식
- 다변수 정규분포의 pdf 정의와, 자연로그의 성질을 이용하면, 아래와 같이 계산된다.

- 위 전개한 마지막 식으로부터 q(x_t-1 | x_t) gaussian의 평균(파란색)과 분산(빨간색)을 정리해보면, 아래와 같다.
- 분산 / 평균 순서

- 최종적으로, 계산으로 도출한
q(x_t-1|x_t)의 평균과 분산은 아래와 같다! 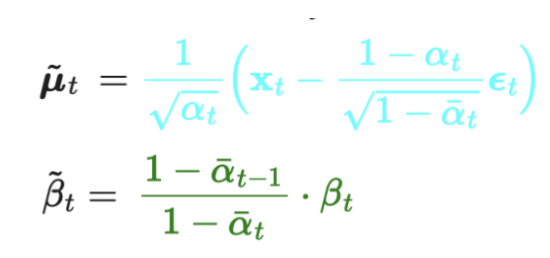
- 결론적으로, 우리는 q(x_t-1 | x_t) gaussian의
- 분산은 알파(베타) 값만 필요하므로, 이미 알고 있는 값이고,
- 평균은
ϵ_t만 우리가 구할 수 있으면 알 수 있다.
- 왜냐, 알파(베타)는 forward process에서 sampling해서 쓴 것을 그대로 다시 이용하는 것이기 때문이다!
- 그러므로 우리는, (q(x_t-1 | x_t)을 직접 구할 수 없어 이를 근사한)
P_theta(x_t-1|x_t)가ϵ_t을 정확히 출력하도록 학습할 수 있다면,- 우리는 q(x_t-1 | x_t)를 알 수 있게 되고,
- noise된 이미지의 noise를 제거할 수 있게 된다!
- 다른 말로 하면, diffusion 학습을 완료하면,
- inference 시, 완전한 normal distribution으로부터 샘플링한 값으로부터, 새로운 이미지를 생성할 수 있다는 뜻!
- 우리는 q(x_t-1 | x_t)를 알 수 있게 되고,
- 그럼 우리는 이제,
P_theta(x_t-1|x_t)가ϵ_t을 정확히 근사하여 출력하도록 학습 하는 방법을 알아보자.- 이를 위해서, 우리는
P_theta(x_t-1|x_t)가ϵ_t을 정확히 근사하도록 학습하기 위한Objective(Loss) Function을 알아보자.
- 이를 위해서, 우리는
학습 가능한 형태의 loss fuction 유도하기
- 위에서 구한 Loss Function은 아래와 표현 가능하다.

- 좀 더 정확히는 아래와 같이 유도 가능하다.

simplification?
- 여기서 t는 1과 T 사이에서 uniform하다.
- Simplified objective는 기존의 training objective에서 가중치를 제거한 형태
- 이 가중치항은 t에 대한 함수로, t가 작을수록 큰 값을 가지기 때문에
- t가 작을 때 더 큰 가중치가 부여되어 학습된다.
- 즉, 매우 작은 양의 noise가 있는 데이터에서 noise를 제거하는데 집중되어 학습된다.
- 따라서 매우 작은 t에서는 학습이 잘 진행되지만, 큰 t에서는 학습이 잘 되지 않기 때문에
- 가중치항을 제거하여 큰 t 에서도 학습이 잘 진행되도록 한다.
전체 training/inference 과정 정리

- sampling = inference 인 것으로 보임

- TODO: 아래 1줄 이해하기
- sampling과정은, (데이터 밀도의 학습된 기울기로 ϵθ 을 사용하는) Langevin dynamics와 유사하다고 한다.
- 위 samping의 4번 식이 왜 저렇게 되는지 이유
- network를 통해 구한 ϵ를 이용하면, q(x_t-1 | x_t) gaussian의 평균을 알 수 있습니다.
- 또한, q(x_t-1 | x_t) gaussian의 variance는 원래 알 수 있습니다.
- 위 4번 식은, 평균에 분산을 더한 겁니다.
Parameterization of Bt
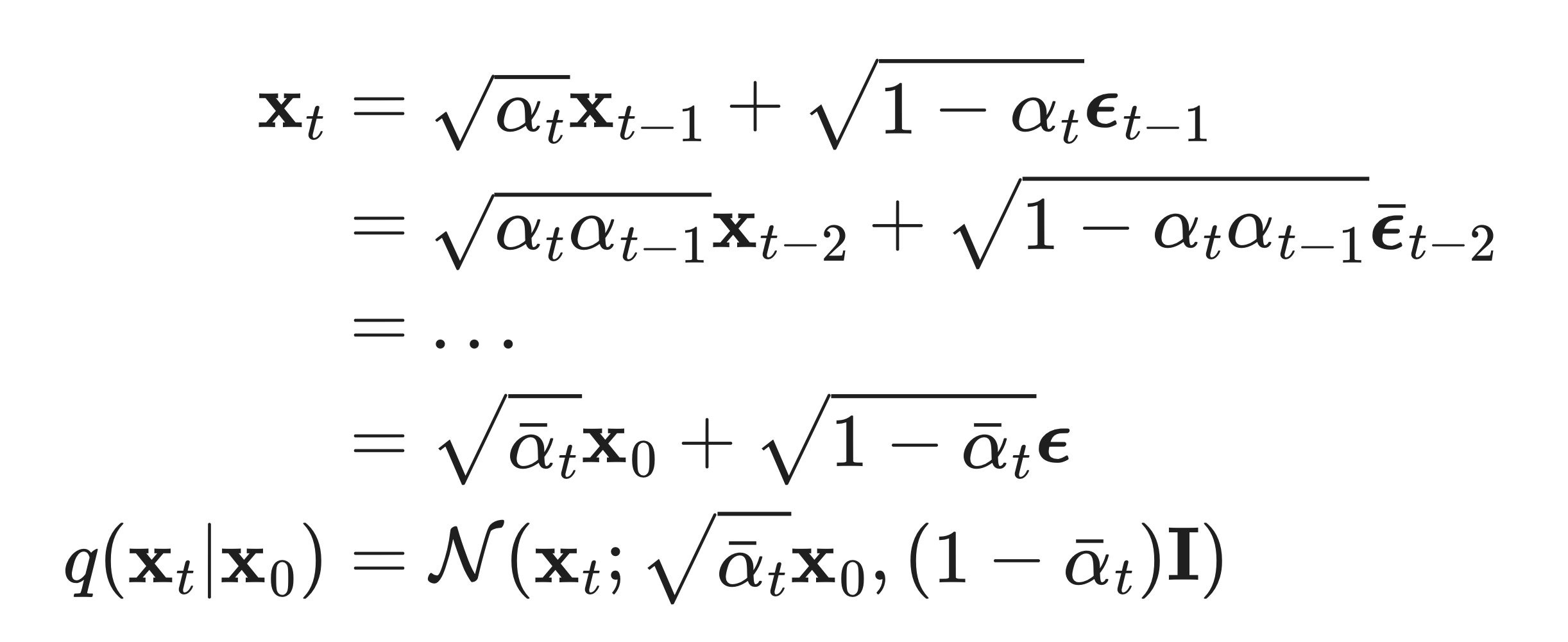
- forward process의 수식에서, variance(Bt)를 t의 변화에 따라 스케쥴링 하는 것이 중요합니다.
- DDPM에서는 선형적인 schedle를 도입했습니다.
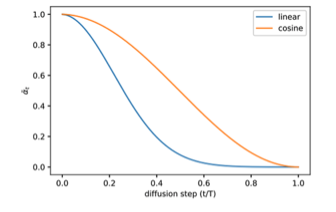
- 위 그림의 파란색 스케쥴

Parameterization of reverse process variance ∑θ
들어가기전에: 복습
reverse process의 목표
L_simple
L_VLB
본문
- DDPM에서는 βₜ를 학습 가능한 상태로 만드는 대신 상수로 고정하고, Σₜ(xₜ, t)을 다음과 같이 설정했습니다:
- Σₜ(xₜ, t) = σₜ²I
- 여기서 σₜ는 학습되지 않고 , σₜ= βₜ
- 이는 대각 분산 Σₜ를 학습하면 학습이 불안정해지고 샘플 품질이 저하된다고 판단했기 때문입니다.
Noise-Conditioned Score Network(NCSN) 과의 관계
- diffusion model의 특정 parameterization (reverse process로 추정됨)이,
- 학습 중 여러 noise 레벨에서의
denoising score matching과 비슷하다. - Lagevin Dynamics 문제를 푸는 것과 동등하다.
- 학습 중 여러 noise 레벨에서의
- TODO
- 아래 부분은 이해가 완벽하지 않아서, 내용이 부정확할 수 있음.

Stochastic Gradient Lagenvin Dynamics ?
- Stochastic Gradient Descent의 변형이라고 보면 된다.
- SGLD는 parameter update 시 Gaussian Noise를 주입한다.
- SLDG에서 noise term을 추가하는 이유?
- SGD가 local minima에 빠지는 단점을 극복하기 위해,
- SGLD의 수식은 아래와 같다.

- 한번에 많이 update하려 할수록, noise 주입도 커진다.

- SGLD와 Diffusion Process는 어떤 연관이 있는가?
- 확산 모델의 forward 과정에서도
Langevin Dynamics의 아이디어를 적용하여 노이즈를 추가
- 확산 모델의 forward 과정에서도
NCSN ?
- 위 Langevin dynamics의
∇xlogq(x)를 딥러닝 네트워크로 학습하는 방법 - 점수 기반 생성 모델링(score-based generative modeling) 방법을 제안했다.
- forward diffusion process 의 경우
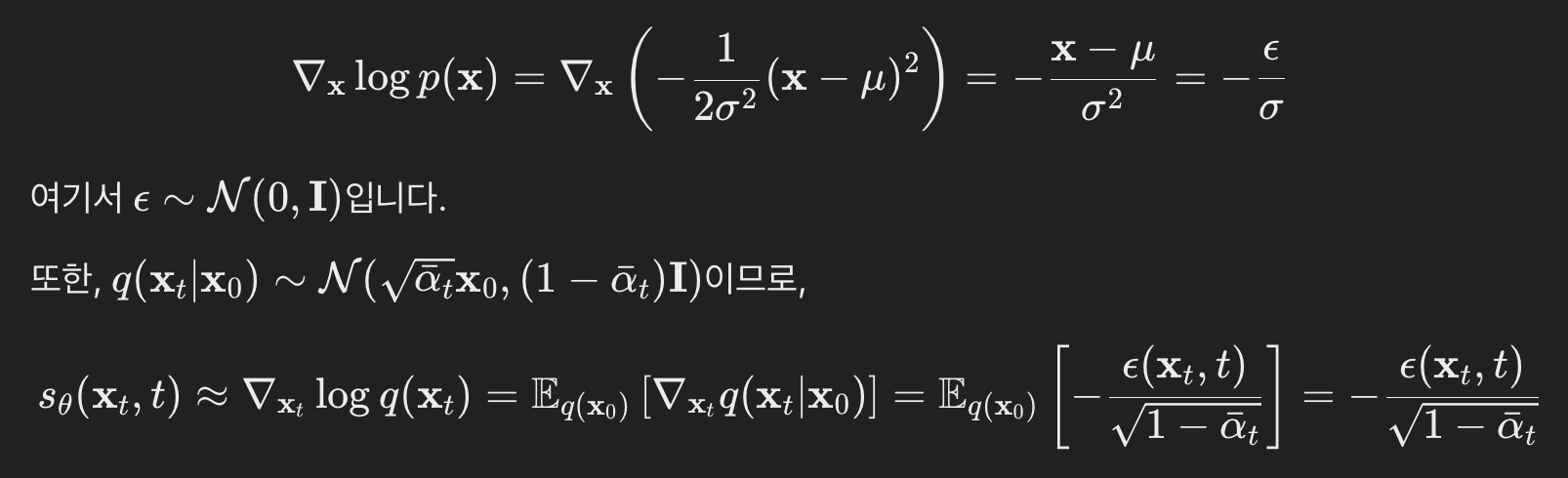
- 우리는 실제로 reverse diffusion process에서 ϵ를 추정하도록 학습합니다.
- 다른 말로,
∇xlogq(x)를 딥러닝 네트워크로 학습한다고 볼 수 있습니다.
- 위 식을 SGLD에 대입하여, 서서히 이미지에 노이즈를 주입할 수 있습니다.
- SGLD에 noise term이 있는 이유?
- 데이터는 사실 고차원 공간에 골고루 퍼져 있는 것처럼 보이지만, 실제로는 훨씬 더 낮은 차원의 구조(즉, 얇은 층이나 표면)에 집중되어 있는 경우가 많습니다.
- 이를 매니폴드 가설이라고 부릅니다.
- 이로 인해, 데이터가 드문 곳에서는 분포를 정확히 추정하기가 어렵고, 점수 계산(예: 데이터 분포의 기울기)을 덜 신뢰할 수 있게 됩니다.
- 이를 해결하기 위해 작은 Gaussian 노이즈(랜덤 노이즈)를 데이터에 추가해 고차원 공간 전체에 데이터가 골고루 분포된 것처럼 보이게 만듭니다.
- 이렇게 하면 점수를 추정하는 네트워크가 안정적으로 학습할 수 있습니다.
TODO: 이해 실패한 부분
- DDPM은 고품질의 샘플을 생성하지만 다른 likelihood 기반의 모델보다 경쟁력 있는 log likelihood가 없다.
- DDPM의 lossless codelength가 대부분 인지할 수 없는 이미지 세부 정보를 설명하는 데 사용되었다.
- Diffusion model의 샘플링이 autoregressive model의 디코딩과 유사한 점진적 디코딩이라는 것을 보였다.