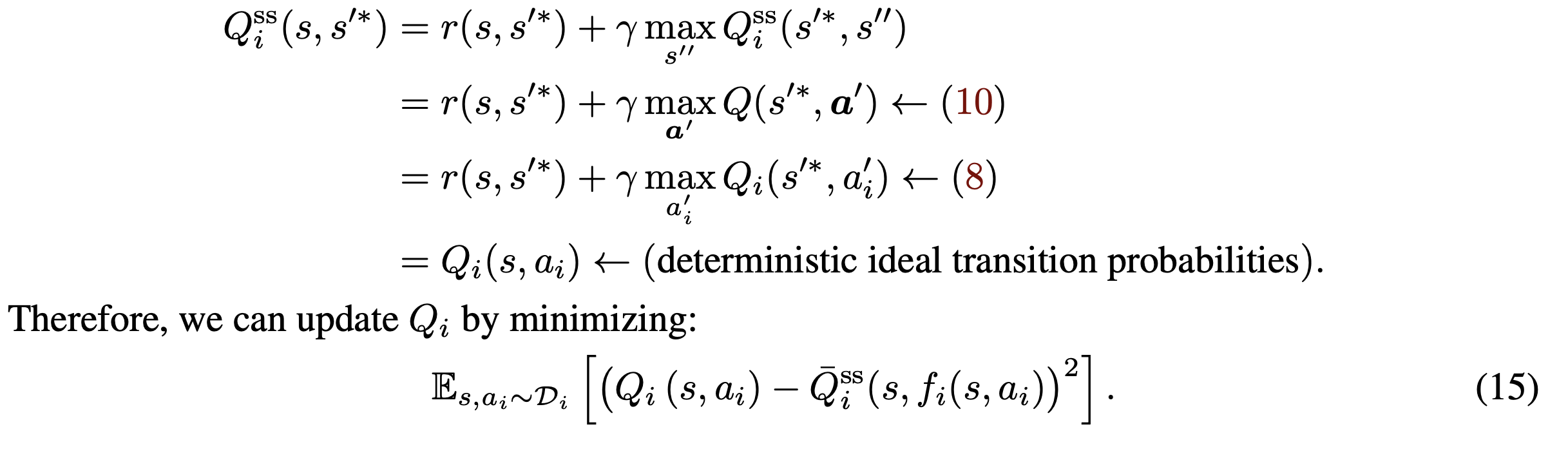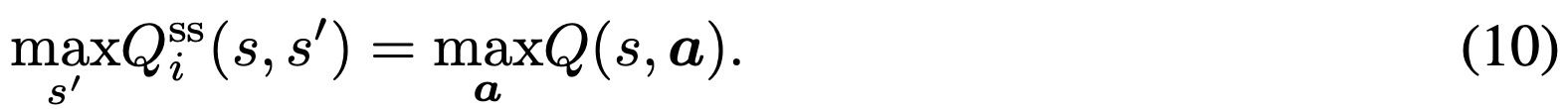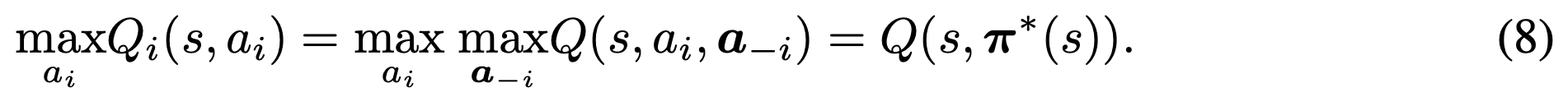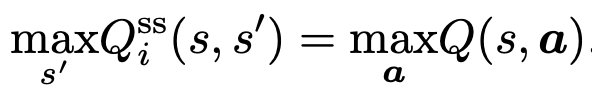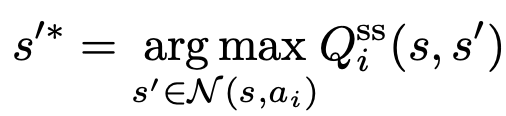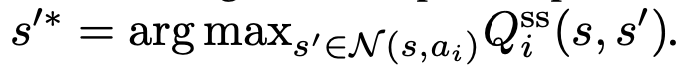DTDE 왜 해야함???
- 논문에서 언급한 fully decentralized MARL의 중요성 3가지
- centralized learner가 없어도 되니, 더 applicable/cleaner/easier.
- individual learners가 다른 agents 수에 무관하기 때문에, 확장성이 더 좋습니다. (better scalability)
- TODO: 학습되지 않은 다른 agents(e.g. 사람)들의 존재에 대해 좀 더 robust 합니다.
- 내가 이 논문을 구현해보는 이유?
- 내 application에서, CTDE랑 성능이 비슷하면, 굳이 CTDE를 할 필요가 없다.
- 학습 속도도 느리고, multi agent data 수집 과정도 복잡해지기 때문
- CTDE는 agent 수가 증가함에 따라, joint action space의 수가 폭발적으로 증가하기 떄문에, 학습에 어려움이 생깁니다. 그러므로, agent 수가 많은 MARL문제의 경우, DTDE은 CTDE에 비해 성능이 좋을 수 있습니다.
- COMA와 같은 해결책들은, 이론적으로 수렴이 증명된 방법이라기 보단, 실험적으로 잘 되는 경우입니다.
- 다른 agents(사람) 들은 시뮬레이터에서 모델링하기 어려운데, 서로 충돌하지 않고 싶어하는 공동의 목표가 있습니다. DTDE가 CTDE보다 (멀티 로봇이 사람에 대해) 더 회피 성능이 더 좋은지 확인해보려 합니다.
- 해석 (풋살)
- DTDE
- 우리 풋살 팀이 경기를 하는데 내 안경에 카메라를 들고 비디오를 찍는다. 그리고 경기 후 마다, 혼자 분석을 통해 학습한다.
- 이렇게 연습 경기 5경기를 분석하여 학습한다.
- 그리고 시합 경기를 뛴다.
- CTDE
- 우리 풋살 팀이, 비디오를 통해 BEV 경기화면을 전부 찍은 후, 경기 후 다 같이 모여 분석을 통해 학습한다.
- 이렇게 연습 경기 5경기를 분석하여 학습한다.
- 그리고 시합 경기를 뛴다.
- DTDE 를 CTDE 대신 하면 좋은 점?
- 모든 선수의 시야나 의도를 저장하기 어려우므로, 내껏만 저장해놨다가 학습했을 때 잘되면 좋다.(데이터 수집의 어려움이 줄어든다.)
- 풋살 인원이 5명에서 7명으로 늘었을 때, 혹은 축구를 하게 되었을 때,
- CTDE는 학습이 오래걸릴 수 있고, 차원의 저주로 인해 학습이 안될 수도 있다.
- DTDE
- 커피 배달 로봇들이 최대한 빠르게 물량을 배달하도록 학습하는데,
- 내 센서 정보 뿐만 아니라, 서로의 목적지와 위치/속도 등을 다 공유한 상태로 학습한다. (예: 시뮬레이터에서)
- 그리고 실제 배달시에는, 내 센서로만 주행한다.
- CTDE
- 커피 배달 로봇들이 최대한 빠르게 물량을 배달하도록 학습하는데,
- 서로의 목적지와 위치/속도를 모른 채로 내 센서정보만을 가지고 학습한다.
- 그리고 실제 배달시에는, 내 센서로만 주행한다.
- DTDE 를 CTDE 대신 하면 좋은 점?
- 학습되지 않은 다른 agents(e.g. 사람, 혹은 다른 알고리즘의 로봇, 다른 회사의 자율주행 차)을 마주한다면?
- 시뮬레이터에서는 사람을 정확히 모델링 하는 것이 어렵습니다.
- 시뮬레이터에서는 다른 회사 로봇/차의 주행 알고리즘을 모델링하는 것이 어렵습니다.
Abstract & conclusion
- independent Q-learning이 decentralized training에 많이 쓰이지만, 아래의 이유로 수렴이 보장되지 않음
- 아래의 이유로 transition probabilities가 non-stationary(통계적 특성이, 시간의 흐름이 따라 변함)
- 다른 agents가 policies를 동시에 update하기 때문에
- 해석
- 경기 1에 내가 한 백패스(a_i_t)의 결과로 우리팀 선수들이 후진했어(s_t+1).
- 하지만, 경기 5에는 내가 한 백패스(a_i_t)의 결과로 우리팀 선수들이 전진했어(s_t+1).
- 즉, 내가 같은 행동을 해도, (내 행동을 통한 결과로) 가능한 next state의 분포는 경기가 거듭됨에 따라 달라진다.(non-stationary)
- 그래서, 이런식으로 학습하면, 내가 경기들을 통해 실력이 늠을 보장할 수 없어.
- 이런식으로 학습? 구체적으로는 아래 과정임
- 경기 비디오를 멈추고, 이 상황에서 내가 한 행동과 그 보상, 그리고 그 다음 frame의 상황을 얻어
- 이를 기반으로
- 내가 이 scene에서 한 행동의 가치 = (보상 + 다음 frame에서 내가 생각하는 최고 좋은 행동의 가치)
- 근데, 내 같은 행동으로 인해, 1번째 경기 영상에서 유발되는 다음 frame 장면과, 2번째 경기에서 유발되는 다음 frame 장면이 다름. (왜냐면 선수들의 실력이 성장하고 있기 때문에)
- 이로 인해, 내 행동의 가치 판단을 배우기가 어려움.
- 논문에서 제안하는 내용
- stationary ideal transition probabilities 제안
- ideal transition function을 모델링 함으로써
- 다른 agents의 학습된 policies와 독립적임.
다른 agents의 optimal conditional joint policy에 의존적임.
다른 agents의 optimal conditional joint policy는 내 agent의 action에 의존적
- independent Q-learning이 수렴할 수 있게 함
- Ideal Independent Q-learning (I2Q) 제안
- fully decentralized method
- independent Q-learning가 modeled ideal transition function에서 수행되어, 수렴할 수 있게 함.
- deterministic 환경에서 optimal 수렴을 하는 것을 이론적으로 증명함.
- 모든 agents가 각각의 ideal transition probabilities에서 독립적으로 Q-learning을 수행한다면, 그들의 policies들은 optimal joint policy로 수렴함을 증명했습니다.
- 실험적으로, 다양한 stochastic MARL 환경에서 어느정도 성능이 나옴을 입증함.
- 이론적으로, value gap을 분석했습니다
- 아직, CTDE(e.g. QMIX) 의 성능에 미치친 못합니다.
- 해석
- 조건: 전반전에 내가 한 백패스(a_i_t)의 결과 분포와, 후반전에는 내가 한 백패스(a_i_t)의 결과 분포가 같은 상황에서,
- 내 풋살 실력을 학습하면, 일관되게 풋살 실력이 증가할 것으로 기대!
- 위 조건을 어떻게 구현하나면, 내 주변 동료들이 항상 messi처럼 플레이하는 모델을 학습하자!
- 구체적 학습 방법
- 동영상을 멈추고, 그때의 상황과 내가 한 행동, 그리고 얻게 된 보상 3개만 가지고 학습할꺼야.
- 그 상황에서 내가 한 행동의 가치 = (보상 + (내 행동으로 인해 내 주변 메시들이 움직인 후의 next state에서, 내가 생각하는 제일 좋은 행동을 했을 때의 가치) )
- 이렇게 하면 좋은게, 1번째 경기던 5번째 경기던, next state는 주변 선수들이 메시라고 가정하고 상상하는 것이기 때문에, 데이터가 일관됩니다!
Introduction
- 각 agent의 ideal transition probabilities는 학습하기 전 사전에 알 수 없지만, decentralized way로 의도적으로 학습될 수 있습니다.
- 원문: We let each agent learn the QSS-value [6], the value of state and next state, which will converge on its replay buffer and be equivalent with the optimal joint Q-value in deterministic environments. (아래 3줄)
- 각 agent가 QSS-value([6], state 과 next state의 value)를 학습하게 함.
- https://velog.io/@jk01019/Estimating-Qs-s-with-Deep-Deterministic-Dynamics-Gradients
- replay buffer에서 converge할 것임.
- deterministic 환경에서의 optimal joint Q-value와 같음.
- 그러므로, 각 agent의 next state는 highest QSS-value를 가진 값이다.
- a state와 an action이 주어진 ideal transition probabilities 상황에서
- 원문 (위 2줄)
- Then, for each agent, the next state under ideal transition probabilities, given a state and an action, is the one with the highest QSS-value.
- 그러므로, 각 agent는 ideal transition function을 아래 방식으로 모델링할 수 있다.
- 해석
- 비디오를 보기 전, 내 패스에 메시들이 어떻게 움직일지 알 순 없습니다.
- 하지만 내가 비디오를 보면서, 메시들의 움직임 상상 능력을 키울 수 있습니다.
- 각자 집에서 비디오를 보면서, 현재 frame -> 다음 frame 가치 평가 능력을 열심히 키우면,
- 경기를 거듭할수록 -> 내가 가장 높게 평가한 다음 frame이, 개인이 아닌 팀을 위한 최고의 상황에 가까워집니다.
- 학습을 거듭할수록 내 행동에 대한 메시의 움직임 예측은, 아래와 같아집니다.
- 다음 Frame을 예측하는 상상 중, 최고의 frame 상상한 결과
CTDE
- 아래 방법들은, 학습 시 all agents의 정보에 접근 가능.
- 수학적 수렴이 보장된 방법들
policy-based methods
- policy optimization objectives를 다르게 디자인 함으로써
- 15, 8, 32, 37, 25, 18
- 32
- 37
- 25
- 18
Value factorization methods
- joint value function을 individual value functions로 분해함. (Individual-Global-Max Condition을 통해)
- 26
- 22
- 24
- 31
- 21
DTDE
- 우리의 논문은, off-policy로 작동 가능하다.
- 정보 공유도 일절 하지 않는다.
Method
Preliminaries

- 논문에서, 우리는 Q* 대신 Q로 편의상 쓸 것이다. (Optimal Value를 의미)
- 개별 agent 입장에서 보면, transition probability는 아래.
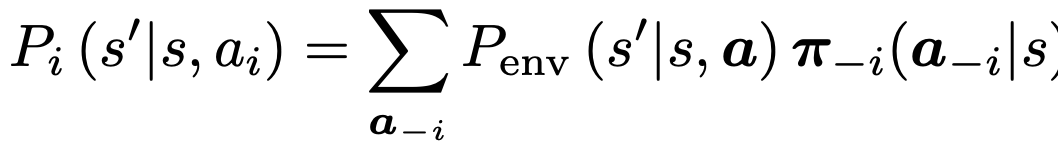
- transition probability는 다른 agent의 polices에 의존합니다.
- 다른 agent가 policies를 연속적으로 업데이트 하기 때문에, Pi는 학습 동안 non-stationary.
- 만약 Qi 업데이트를 DTDE 세팅에서
- off-policy로 하면
- 다른 agent의 actions를 buffer에서 가져오지 못하므로, 다른 agents의 평균적 policeies에 의존한다고 생각할 수 있다. -> non-stationary + outdated 문제!
- on-policy로 하면
- 각 agent는 independent Q-learning을 아래와 같이 수행함
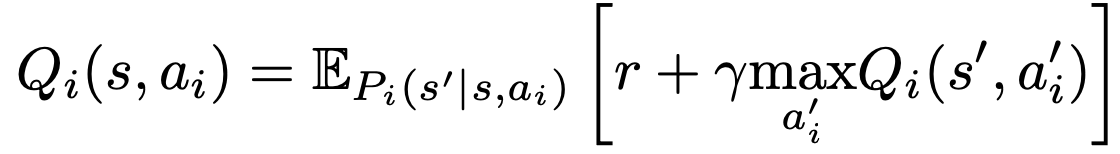
Ideal Transition Probabilities
- 풀고자 하는 문제:
non-stationary를 어떻게 해결할 것인가?
수학적 배경
- 가정
- optimal joint policy가 1개 뿐이다. (deterministic)
- Q: joint Q-function
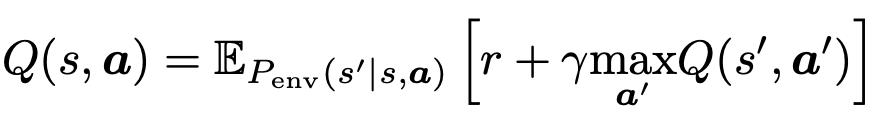
- 가정을 기반으로, optimal joint policy는
deterministic optimal individual policies로 유일하게 factorized 될 수 있습니다.
- 그러므로,
다른 agents의 deterministic optimal joint policy는 (a_i conditioned)
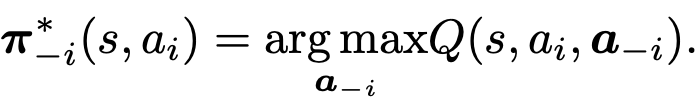
다른 agents의 deterministic optimal joint policy는 여러개가 될 수 있다. 우리는 그중에서 임의로 하나 고를 수 있다.
- 만약 모든 다른 agents가
deterministic optimal joint policy로 행동한다면,
agent i의 transition probabilities는 아래의 ideal transition probability가 됩니다.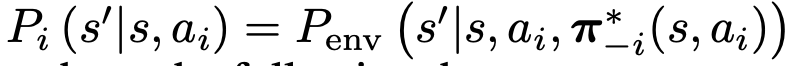
Theorem 1
- 만약 agent i가 ideal transition probabilities(under conditioned with i`s action) 에서 Q-learning을 수행한다면, agent i의 policy는 optimal individual policy로 수렴합니다.
- 만약 모든 agents가 개별적으로 ideal transition probabilities에서 Q-learning을 수행한다면,
- 모든 agents들은 각각의 optimal individual policies로 수렴할 것이고 -> optimal joint policy에 도달합니다
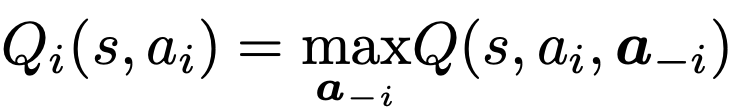
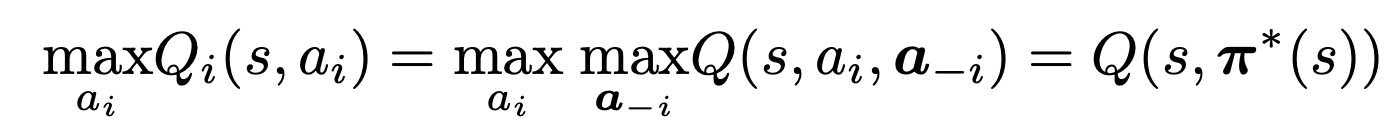
- 해석
- 1.
- 내가 집에서 비디오를 보면서, 내 행동을 학습할 때,
- next frame 기반 학습이 아니라, 주변 동료들이 메시라고 가정하고 next frame을 상상하여 학습한다면,
- 나는 내 행동을 매우 잘 평가할 수 있게 됩니다.
- 2.
- 만약 우리팀원 모두가 집에가서 자신의 비디오를 보면서 위 학습을 진행한다면,
- 우리는 경기를 치뤘을 때 최고의 팀에 도달합니다.
I2Q
각 agent를 위한 non-stationary replay buffer로부터, 어떻게 ideal transition probabilities를 얻을 것인가?
1~5번째 경기 비디오로 부터, 어떻게 ```내 행동에 일관되게 반응하는 환경```을 얻을 수 있을까?
- 가정
- QSS-learning [6] 기반
- https://proceedings.mlr.press/v119/edwards20a.html
- https://velog.io/@jk01019/Estimating-Qs-s-with-Deep-Deterministic-Dynamics-Gradients
- 2020 / 16 인용
- 각 agent i는 value function을 자신만의 replay buffer의 경험으로부터 아래와 같이 학습함.
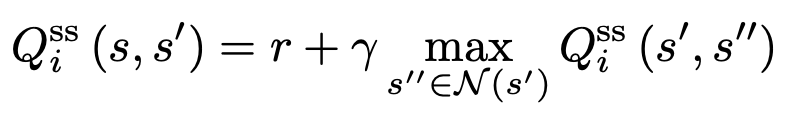
- N (s′) is the neighboring state set of the state s′ (the set of all next states of s′).
- 이 value function 기반 학습 방법의 장점들 (
모든 agents들이 독립적으로 Q_i^ss를 학습하여도 -> agents의 학습된 policies간 optimal consensus를 형성할 수 있는 이유)
- 장점 1
- max QSS를 학습하는 것과, 일반적 max Q(s,a)를 학습하는것은, 같다는 것이 증명됨
- 이 뜻은, optimal joint policy 상황에서, agent i는 (위 식의 좌변을 따라서)
독립적으로 next state를 추론할 수 있다는 뜻
- 장점 2
- Q_i^ss는 (다른 agent의 정보 없이) 각각의 replay buffer만을 사용함에도, 아래의 이유로 optimal value로 수렴할 수 있다.
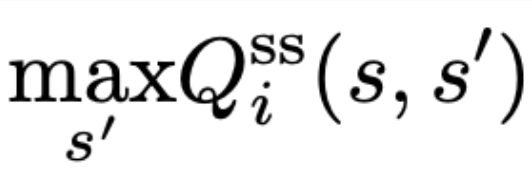 가 action i와 value가 분리시켜주기 때문에,
가 action i와 value가 분리시켜주기 때문에,- implied transition probability
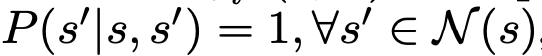 가 항상 stationary 하기 때문에
가 항상 stationary 하기 때문에
- 장점 3
- 모든 agent가 같은 환경에서 움직이므로, 그들은 (각각의 replay buffer에) 같은 state set과 next state set을 모읍니다.
Q_i^ss로부터, 어떻게 ideal transition function을 build하나?
- 환경과
다른 agents의 optimal conditional joint policy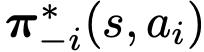 가 determinisitic 하기 때문에,
가 determinisitic 하기 때문에,
- ideal transition probabilities 내에서,
- agent i는 (모든 neighboring states given ai 중에서,) 가장 높은 Q_i^ss의 next state로 deterministic하게 transition한다.
Theorem2
- deterministic 환경에서,
각 agent i가 아래의 transition function 내에서 Q-learning 을 수행한다면, 모든 agent는 optimal policies로 수렴합니다.
Main algorithm
2가지 가정
- 하나의 optimal joint policy 뿐이다. (하지만, I2Q는 multiple optimal joint policies를 지닌 tasks에도 쉽게 적용가능하다.)
- 환경이 deterministic 하다.
알고리즘
stationary ideal transition function(fi) 모델 / Qi(s,a) network / Qi(s, s') network 를 가지고 있습니다.- target 네트워크도 존재합니다.

- 해석
- 내 행동으로 인해 -> 메시들의 움직임이 어떻게 되는지 학습 (fi)
- 목표: 내 행동에 대한 반응으로, 주변 메시들은 어떻게 움직일지 잘 상상하고 싶어.
- 내 현재 상황에서 다음 상황으로 왔을 때의 가치 평가를 잘 하도록 학습(Qiss)
- 목표: 현재 frame에서 다음 frame로 바뀌었을 때, 그 상황이 얼마나 좋은 것인지 잘 판단하고 싶다!
- 내 행동에 대한 평가를 잘 하도록 학습 (Qi) -> 이게 잘 되면, 나는 경기 잘 뛸 수 있음.
- 목표: 내 행동이 얼마나 잘한 것인지 잘 판단하는 능력을 키우고 싶다!
stationary ideal transition function 모델 학습
s'* = argmax_s'[Q_i^ss(s, s')] = f_i(s, a_i)
- (ideal next state를 도출하는 transition function)
- 우리는
f_i(s, a_i) 를 아래의 방식으로 학습합니다.
- 아래 식을 최대화하는 것이 목표!
현실적으로 가능한 next state 범위 중, 가장 큰 Qi_ss 값을 가진 next ideal state를 예측하도록!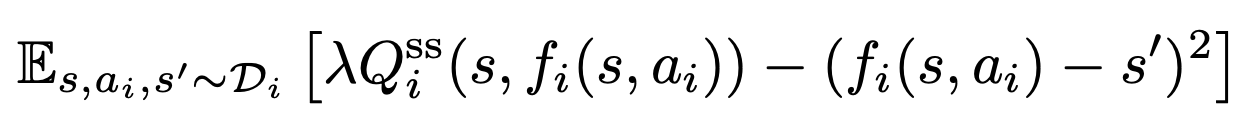 (12)
(12)
- 좌항은 최대화: 모델링의 결과(예측된 next ideal state)가 높은 Q_i^ss 값을 가지도록
- 우항은 최소화: 모델링의 결과(예측된 next ideal state)가 N(s, ai) set 범위 내에서 출력되도록
- 해석
- 목표: 내 행동에 대한 반응으로, 주변 메시들은 어떻게 움직일지 잘 상상하고 싶어.
- 데이터: 풋살 비디오를 멈추고, 현재 scene과 내 행동, 그리고 다음 scene을 가져옵니다.
- 그리고, 내 행동으로 인해 유발될 다음 메시들의 상황(s_i_1^* = fi(s,ai)) 을 상상합니다.
- 1. 내 행동에 따른 메시들 움직임 == ( Q(s, s_i_1^*) 값이 가장 크게 되는 s_i_1^*를 선택하도록) 학습
- 2. 내 행동에 따른 메시들 움직임이, 실제 선수들 움직임(다음 scene)과 차이가 적게 나도록 학습
Qi(s,s') network 학습
- 아래의 TD-error 최소화
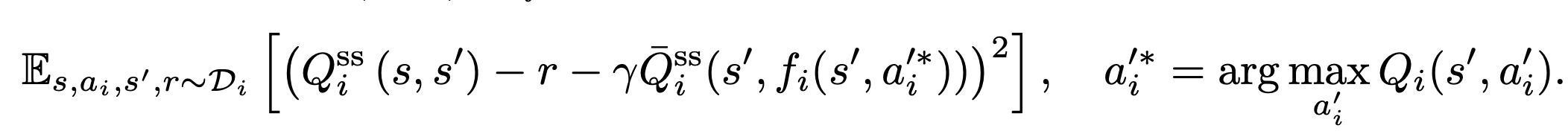 (13)
(13)- 해석
- 목표: 현재 frame에서 다음 frame로 바뀌었을 때, 그 상황이 얼마나 좋은 것인지 잘 판단하고 싶다!
- 데이터: 풋살 비디오를 멈추고, 지금 frame과 내 행동, 보상, 그리고 다음 비디오 frame을 가져옴
- 그리고, 다음 frame에서 내가 생각한 최고의 행동을 했을 때, 메시들이 움직인 결과 상상해보기(s'')
- 지금 frame(s)에서 다음 frame(s')으로 간 상황에 대한 평가 =
- 내 보상 + (다음 frame(s')에서 -> 메시들의 움직임 결과(s``)에 대한 내 평가)
Qi(s,ai) network 학습
- 아래의 TD-error 최소화
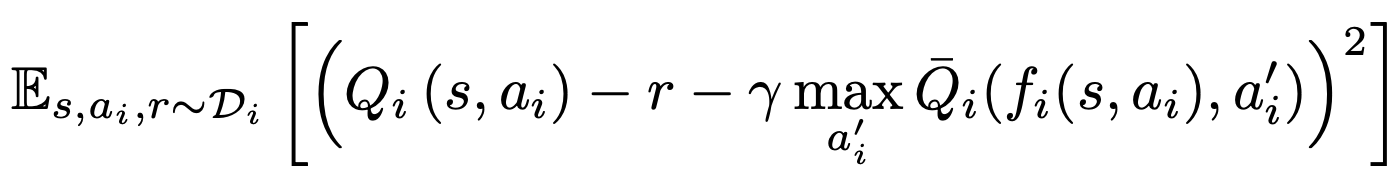 (14)
(14)- 주목할점: replay buffer로부터 s, ai, r 만 쓰인다. (s' 안쓰인다.)
- r(s)라고 가정했는데, r(s, si)이라면,
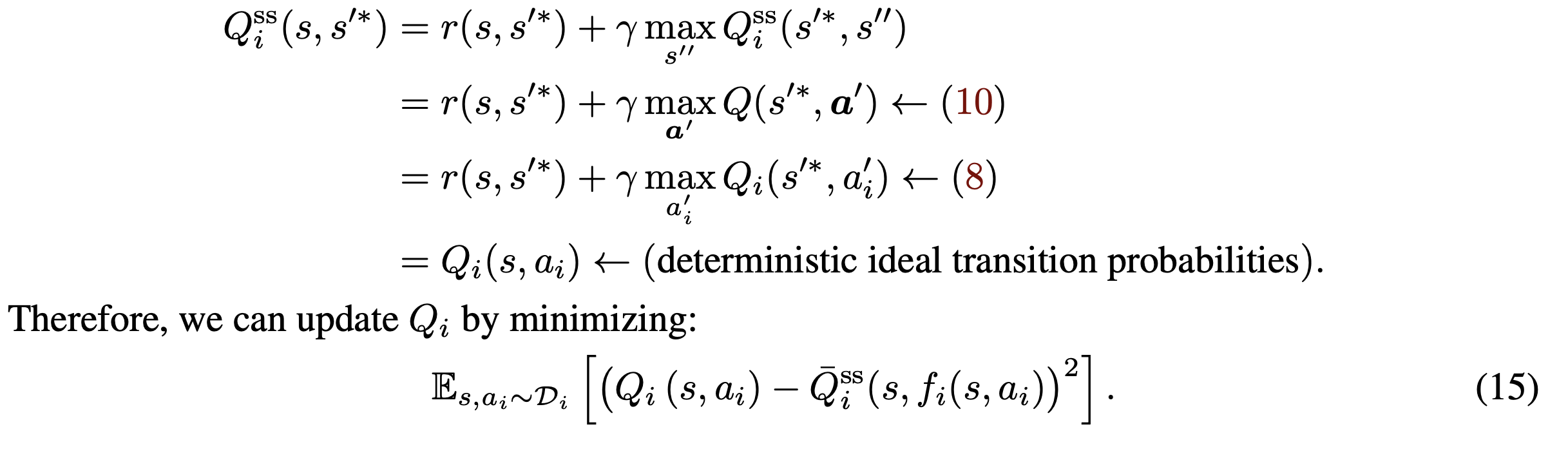
- 식 10 (환경이 deterministic 할 때)
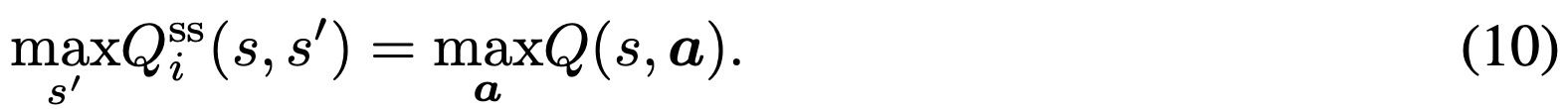
- 식 8 (optimal joint policy는 늘 1개다)
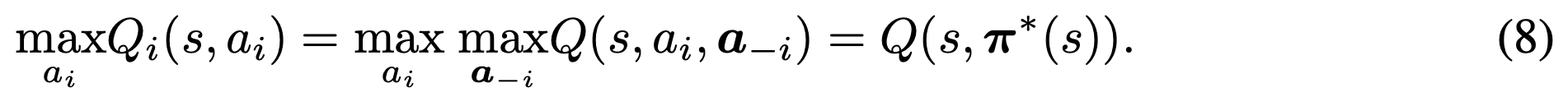
- 14번 식 해석
- 목표: 내 행동이 얼마나 잘한 것인지 잘 판단하는 능력을 키우고 싶다!
- 데이터: 풋살 비디오 멈추고, 현재 frame과 내 행동, 그리고 보상만 가져와.
- 내 행동의 가치는,
- 보상 + (내 행동으로 인한 메시들의 상상 반응 (next state)에서, 내가 생각한 최고 행동의 가치)
- 목표: 현재 frame에서 다음 frame로 바뀌었을 때, 그 상황이 얼마나 좋은 것인지 잘 판단하고 싶다!
- 데이터: 풋살 비디오를 멈추고, 지금 frame과 내 행동만 가져옴
- 그리고, 현재 frame에서 내행동을 했을 때, 메시들이 움직인 결과 상상해보기(fi(s,ai))
- 지금 frame(s)에서 다음 frame(s')으로 간 상황에 대한 평가 =
- 내 보상 + (지금 frame(s)에서 -> 메시들의 움직임 결과(s`*)에 대한 내 평가)
- [현재 frame -> (최고의 next frame) 상황의 가치]
= 얻는 보상 + [(최고의 next frame) -> (최고의 next next frame) 상황의 가치]
= 얻는 보상 + [(최고의 next frame) 에서 다 같이 최고의 행동 할 때의 가치] <- (10)
<- (이유: 환경이 deterministic 하면, 최고의 집단 행동을 하면 무조건 최고의 상황이 옴)
= 얻는 보상 + [(최고의 next frame) 에서 나 혼자 최고의 행동을 할 때의 가치] <- (8)
<- (이유: 최고의 집단 행동이 1개이면, 나만 최고의 행동을 선택하면, 동료들도 최고의 선택을 하기 때문?)
적용
- I2Q는 discrete / continuous state-action space에서 모두 작동한다.


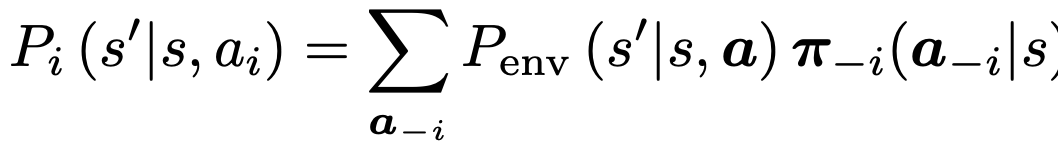
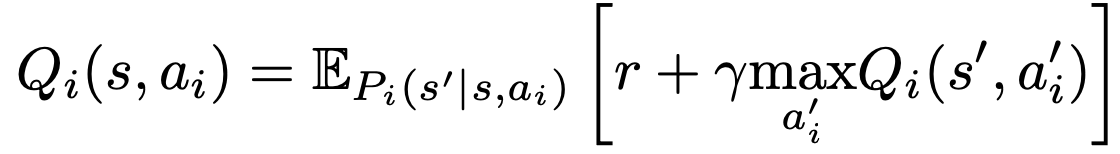
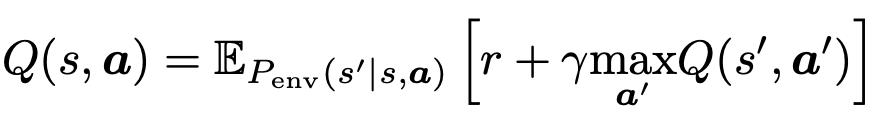
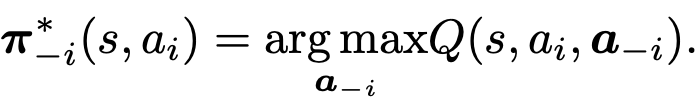
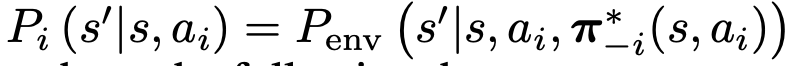
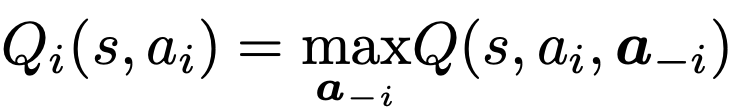
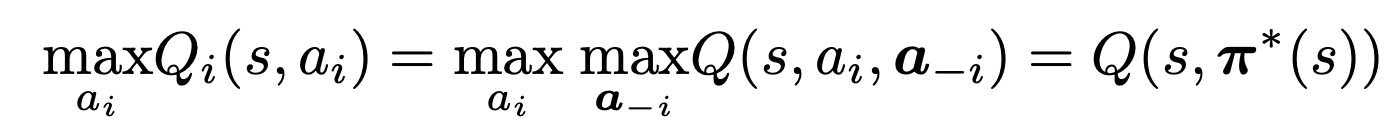
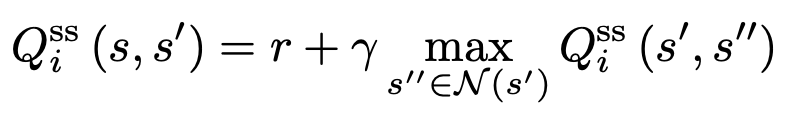
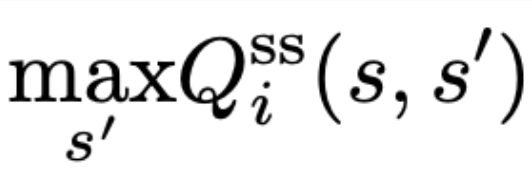 가 action i와 value가 분리시켜주기 때문에,
가 action i와 value가 분리시켜주기 때문에,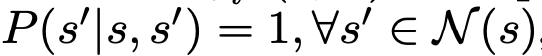 가 항상 stationary 하기 때문에
가 항상 stationary 하기 때문에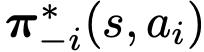 가 determinisitic 하기 때문에,
가 determinisitic 하기 때문에,
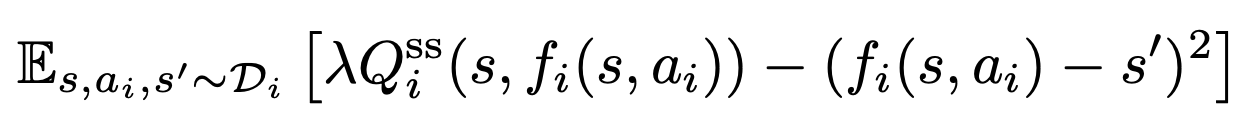 (12)
(12)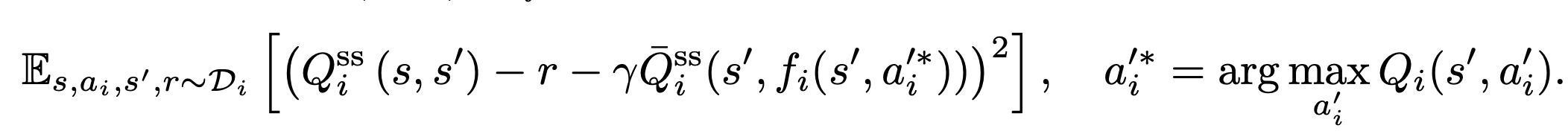 (13)
(13)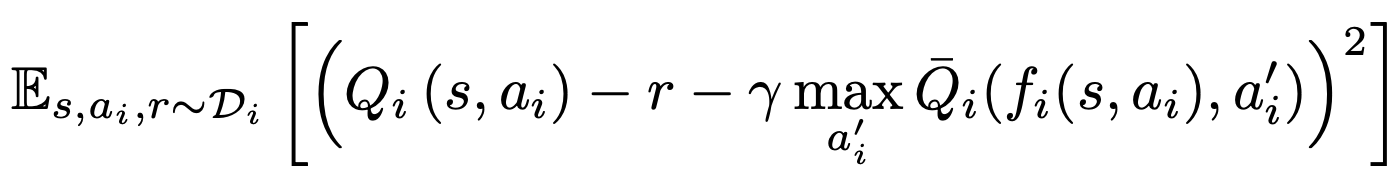 (14)
(14)