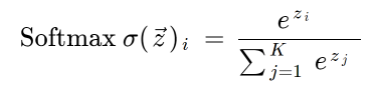[AI Math] 딥러닝 학습 방법

신경망(neural network)

• 선형 모델로는 분류 문제나 복잡한 패턴에서 높은 예측을 구하기 힘듬
• 비선형 모델인 신경망을 고려
• 선형모델과 비선형 함수들의 결합
  
  선형 모델 수식 : $O = X * W + b$
  X (n x d) : 입력 벡터
  W (d x p) : 가중치
  b (n x p) : y절편 들의 행렬
  O (n x p) : 출력 벡터
  $X * W$에서 행렬의 차원이 d에서 p로 바뀜

softmax 연산

모델의 출력을 확률로 해석할 수 있게 변환해주는 연산

$\vec{z}$ 가 출력 벡터 $o$

$softmax(o) = softmax(Wx + b)$

• 주어진 데이터가 어떤 특정한 클래스에 속할 확률이 얼마일지 계산 가능
• 분류 문제를 풀 때 선형 모델과 소프트맥스 함수를 결합하여 예측할 수 있음

import numpy as np

def softmax(vec):
    numerator = np.exp(vec - np.max(vec, axis = -1, keepdims = True)) # 분자
    # max : softmax가 지수함수를 사용하다 보니 너무 큰 벡터가 들어오면 오버플로우가 발생하므로 이를 방지
    denominator = np.sum(numerator, axis = -1, keepdims = True) # 분모
    return numerator / denominator

• 학습할 때는 소프트맥스가 필요하지만 추론 할 때는 원-핫 벡터로 최댓값을 가진 주소만 1로 출력하는 연산을 사용, 굳이 필요하지 않음

활성함수 (activation function)

• 선형 모델의 출력을 비선형으로 바꿔준다
• softmax와 달리 모든 값에 고려하지 않고 해당 주소만 고려하므로 실수 값을 인풋으로 받음
• 선형모델의 출력을 비선형으로 바꿔준 벡터를 잠재 벡터, 히든 벡터 또는 뉴런으로 부름.
  이들로 이루어진 모델이 신경망

sigmoid 함수나 tanh 함수는 많이 쓰이는 활성 함수지만 딥러닝에서는 ReLU 함수를 많이 쓰고 있다.

다층 퍼셉트론 (MLP, multi-layer perceptron) : 선형모델과 활성함수를 반복적으로 사용한 것으로 딥러닝의 기본적인 모형
순전파 (forward propagation) : 다층 퍼셉트론에서 순차적인 신경망 계산, 주어진 입력이 왔을 때 출력물을 내뱉는 과정을 표현한 연산

※ 왜 여러 층을 쌓나

• 이론적으로는 2층 신경망으로도 연속함수를 근사할 수 있음
• 층이 깊을수록 목적함수에 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 줄어들어 효율적인 학습 가능
• 최적화가 쉬운 것은 아님

역전파 알고리즘 (backpropagation)

• 학습에 경사하강법을 적용함, 윗층의 gradient를 계산한 후 점점 밑으로 가면서 역순으로 업데이트하는 방식
• 연쇄법칙 기반의 자동미분(auto-differntiation)을 사용
• 역전파 알고리즘은 순전파 알고리즘보다 더 많은 메모리 사용 → 각 노드의 텐서 값을 컴퓨터가 가지고 있어야함

https://wikidocs.net/150781



[부스트캠프 AI Tech] Week 1 - Day 4