미분
import sympy as sym
x = sym.symbols("x")
sym.diff(sym.poly(x**2 + 2*x + 3), x)경사하강법 알고리즘 (미분)
var = init # init 시작점
grad = gradient(var) # gradient 미분 계산 함수
while(abs(grad) > eps): # eps 알고리즘 종료조건
var = var - lr * grad # lr 학습률, 미분을 통해 업데이트하는 속도 조절
grad = gradient(var)
# 컴퓨터로 계산할 때 미분이 정확히 0이 되지 않으므로 종료조건 필요경사하강법 알고리즘 (벡터)
var = init
grad = gradient(var) # gradient 그레이던트 벡터를 계산하는 함수
while(norm(grad) > eps):
var = var - lr * grad
grad = gradient(var)경사하강법 기반 선형회귀 알고리즘
for t in range(T): # T 학습횟수
error = y - X @ beta
grad = - transpose(X) @ error
beta = beta - lr * grad # lr 학습률- 경사하강법 알고리즘은 정확한 값에 도달할 때까지 수렵하는 것은 아니기 때문에 학습 횟수를 작게 설정하면 목표값에 도달하지 못할 수도 있다.
- 학습률이 작으면 수렴을 늦게 하고 크게 하면 불안정함
- 학습률과 학습횟수를 적절히 조절
비선형회귀의 경우 수렴이 항상 보장되지 않음
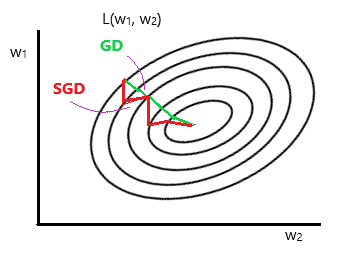
확률적 경사하강법
Stochastic Gradient Descent
- 볼록이 아닌 목적식 최적화 가능
- 경사하강법과 다르게 확률적으로 매번 다른 미니배치를 사용하므로 목적식의 모양이 계속 바뀜
→ 극소, 극대점에 도달해도 탈출 가능
📌 데이터의 일부를 활용하여 업데이트
→ 경사하강법보다 머신러닝 학습에 더 효율적(속도, 메모리 효율, 병렬 연산)
https://wikidocs.net/152765
[부스트캠프 AI Tech] Week 1 - Day 4