📌 재귀(Recursion)

• 자기 자신을 다시 호출하는 것

예시 (별 출력):

def recursion(num):
    if num > 0:
        print('*' * num)
        return recursion(num - 1)  # 자기 자신 호출
    else:
        return 1

실행 결과:

*****
****
***
**
*

📌 실습: 최대공약수 (GCD) - 유클리드 호제법

• 두 자연수 n1, n2 (n1 > n2)에 대해 n1 % n2 = r 이라 하면 n1과 n2의 최대공약수(GCD)는 n2와 r의 최대공약수와 같다.

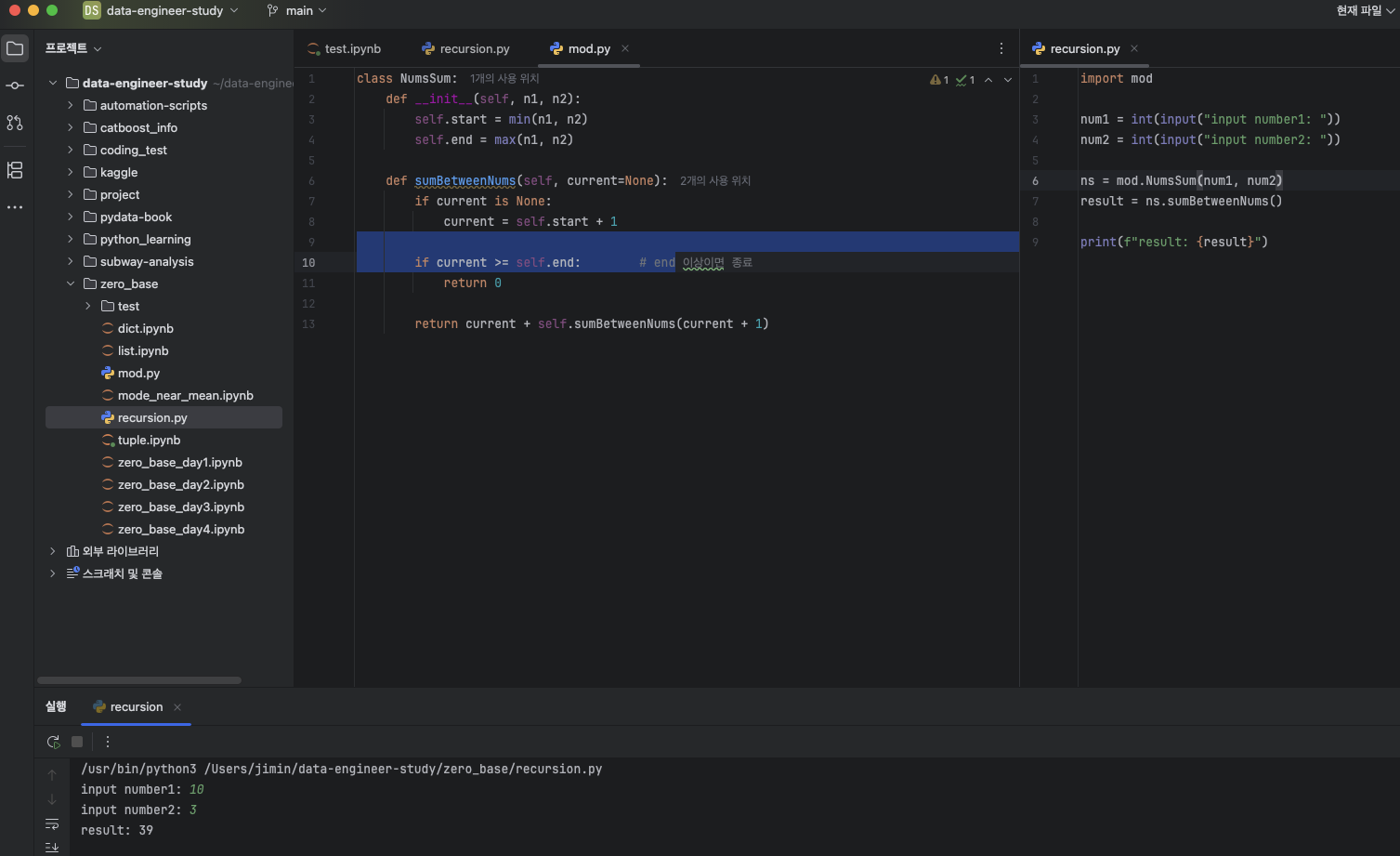
def gcd(n1, n2):
    if n2 == 0:               # 나누어떨어지면
        return n1             # n1이 최대공약수
    else:
        return gcd(n2, n1 % n2)  # 재귀 호출

print(gcd(192, 162))  # 6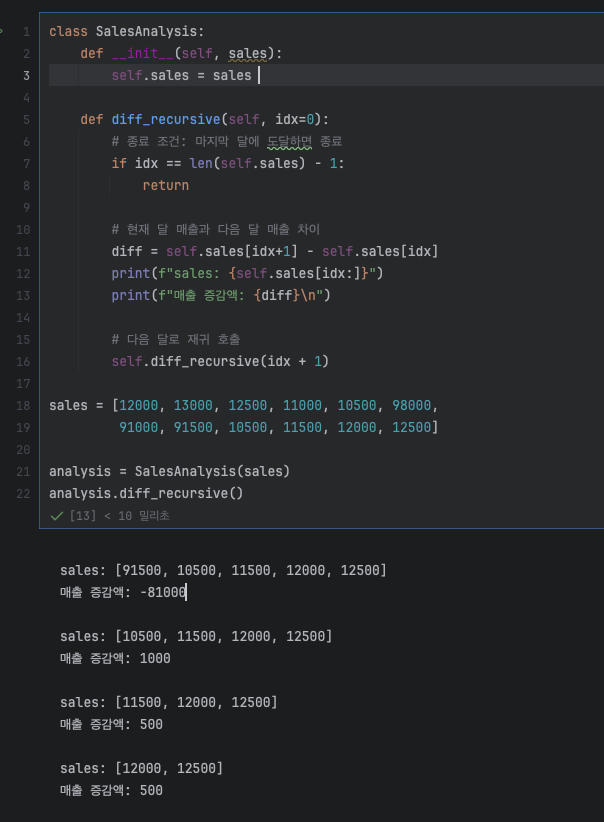

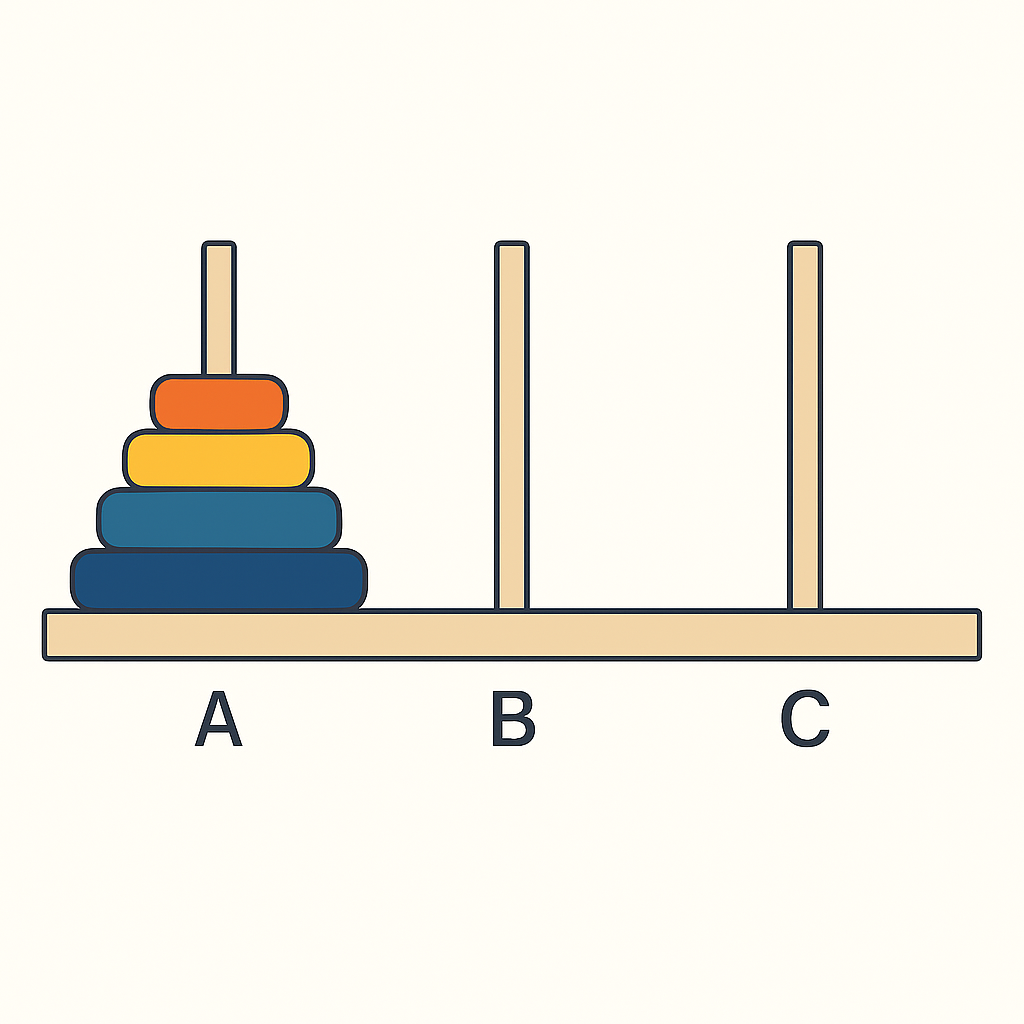
📌 하노이의 탑

• 세 개의 기둥을 이용해 원판을 옮기는 퍼즐
• 규칙:
  1. 한 번에 한 개의 원판만 옮길 수 있다.
  2. 큰 원판은 작은 원판 위에 올려놓을 수 없다.
  

📌 실습: 하노이의 탑 알고리즘

def hanoi(n, start, via, end):
    if n == 1:
        print(f"Move disk 1 from {start} → {end}")
    else:
        hanoi(n-1, start, end, via)                # n-1개를 보조 기둥으로
        print(f"Move disk {n} from {start} → {end}")  # 가장 큰 원판 이동
        hanoi(n-1, via, start, end)                # 보조 기둥 → 목표 기둥

# 실행 예시 (원판 3개)
hanoi(3, 'A', 'B', 'C')

Move disk 1 from A → C
Move disk 2 from A → B
Move disk 1 from C → B
Move disk 3 from A → C
Move disk 1 from B → A
Move disk 2 from B → C
Move disk 1 from A → C

✨ 정리

• 재귀 알고리즘: 자기 자신을 호출해서 문제를 단계적으로 해결
• 최대공약수: 유클리드 호제법으로 재귀 구현 가능
• 하노이의 탑: 분할정복 + 재귀의 대표적 예시