[프로그래머스 / Java] 콜라 문제 #132267

dOcOb·2023년 1월 24일

프로그래머스

목록 보기

1/4

0. 문제 해석

콜라 빈 병 a 개를 가져다주면, 새 콜라 b 개를 돌려주는 가게에, n 개의 콜라를 가져간 후,
그 가게에서 돌려받는 대로 바로 다 마시면서 콜라를 리필할 때, 처음 n 개의 콜라를 제외하고,
가게에서 받은 새 콜라의 개수를 구하는 문제이다.

테스트 케이스

case1: n=20, a=2, b=1
case2: n=20, a=3, b=1
case3: n=50, a=3, b=1

1. My Solution1

이론

아이디어 구상

현실에 가까운 방법으로 문제를 풀어보자.

현재 가지고 있는 콜라를 변수 'currentCoke'로 지정하여 관리한다.
추가로 받은 콜라를 변수 'newCoke'로 지정하고, 입력받은 a,b,n을 이용해서 'newCoke'를 최신화 하며 반복문을 돌린다.

순서

n(currentCoke)을 a로 나누어 몫을 b에 곱한 값을 addCoke로 지정.
addCoke를 이용하여 newCoke, currentCoke를 최신화.
currnetCoke를 사용하여 1,2번을 반복.
currentCoke가 a보다 작아질 때 반복문을 탈출하고, newCoke를 반환.

코드

Solution

public class Coke {

    public int mySolution(int a, int b, int n) {
        int newCoke = 0;
        int currentCoke = n;

        while (true) {

            // 1. n(currentCoke)을 a로 나누어 몫을 b에 곱한 값을 addCoke로 지정.
            int addCoke = currentCoke / a * b;
            int remainder = currentCoke % a;

            // 2. addCoke를 이용하여 newCoke, currentCoke를 최신화.
            newCoke += addCoke;
            currentCoke = addCoke + remainder;

            // 3. currnetCoke를 사용하여 1,2번을 반복.
            if (currentCoke >= a) {
                continue;
            }

            // 4. currentCoke가 a보다 작아질 때 반복문을 탈출하고, newCoke를 반환한다.
            break;
        }

        return newCoke;
    }
}

Test 결과

결과: 성공!

하지만 느낌상 이 문제는 수식 하나로 해결할 수 있는 문제일 것 같다.
곰곰이 생각해보자..😕

2. My Solution2 (실패)

이론

아이디어 구상

콜라가 빈 병이든 새 병이든 새로 얻어지는 콜라의 개수만 구하면 그만이다.
n개의 콜라가 있을 때 다음 새로 얻어지는 콜라의 수는 n * b / a 에 소수점을 버린 정수이다.

아래는, n=20, a=3, b=1 일 때, 정답을 구하는 과정이다.
문제 링크에서 이미지로 제공하는 예시에 새로운 콜라에 노란색으로 표시를 한 그림이다.

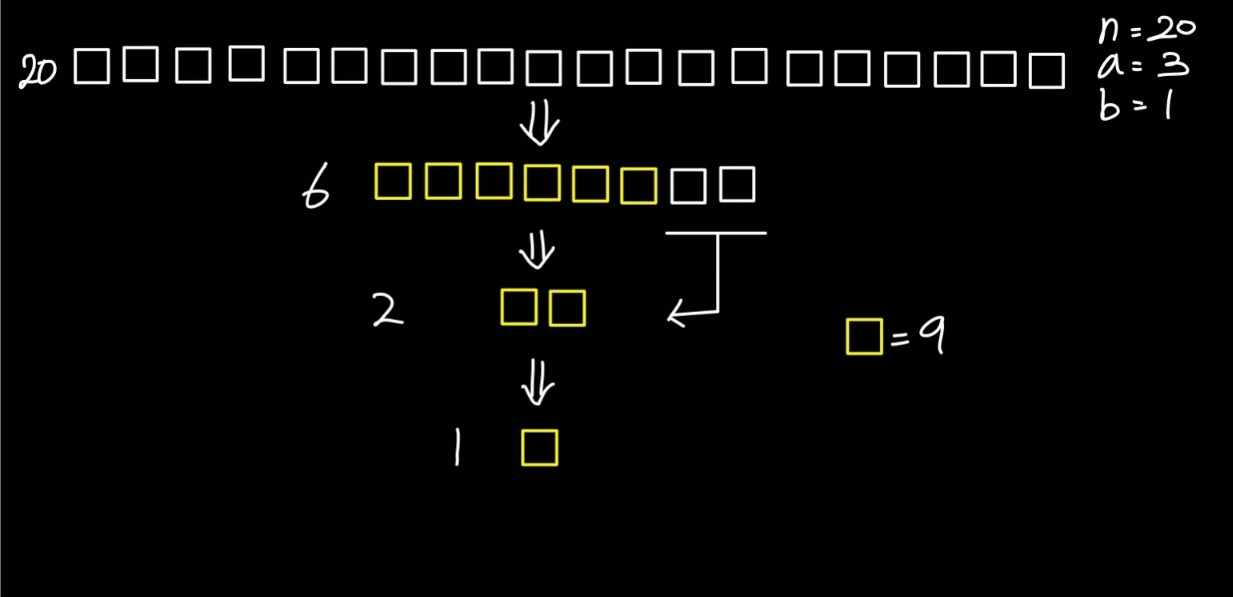
[n=20, a=3, b=1]

그림으로 보니 수학적인 느낌이 안든다. 20을 3으로 나눈 값을 옆에 표시해보자.

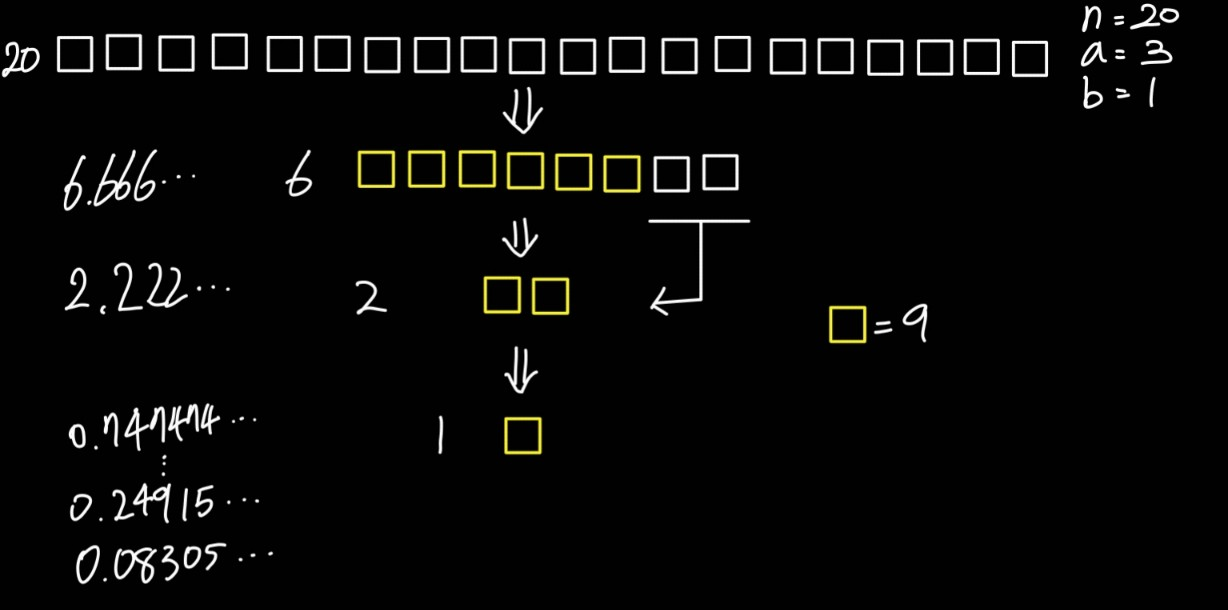
[n=20, a=3, b=1], 숫자 나눈 값 추가

이렇게 보니, 새로운 콜라로 변경되지 못 한 콜라 (흰 네모)에, 새로운 콜라의 가능성을 부여할 수 있을 것 같다.

이번엔 숫자를 50으로 키우고 변하는 숫자만 보자.

아래 그림에 임시 창고는, 새로운 콜라가 되지 못 한 콜라들을 넣어뒀다가, a개가 되면 b개를 main라인에 추가해주기 위한, 콜라 창고이다.

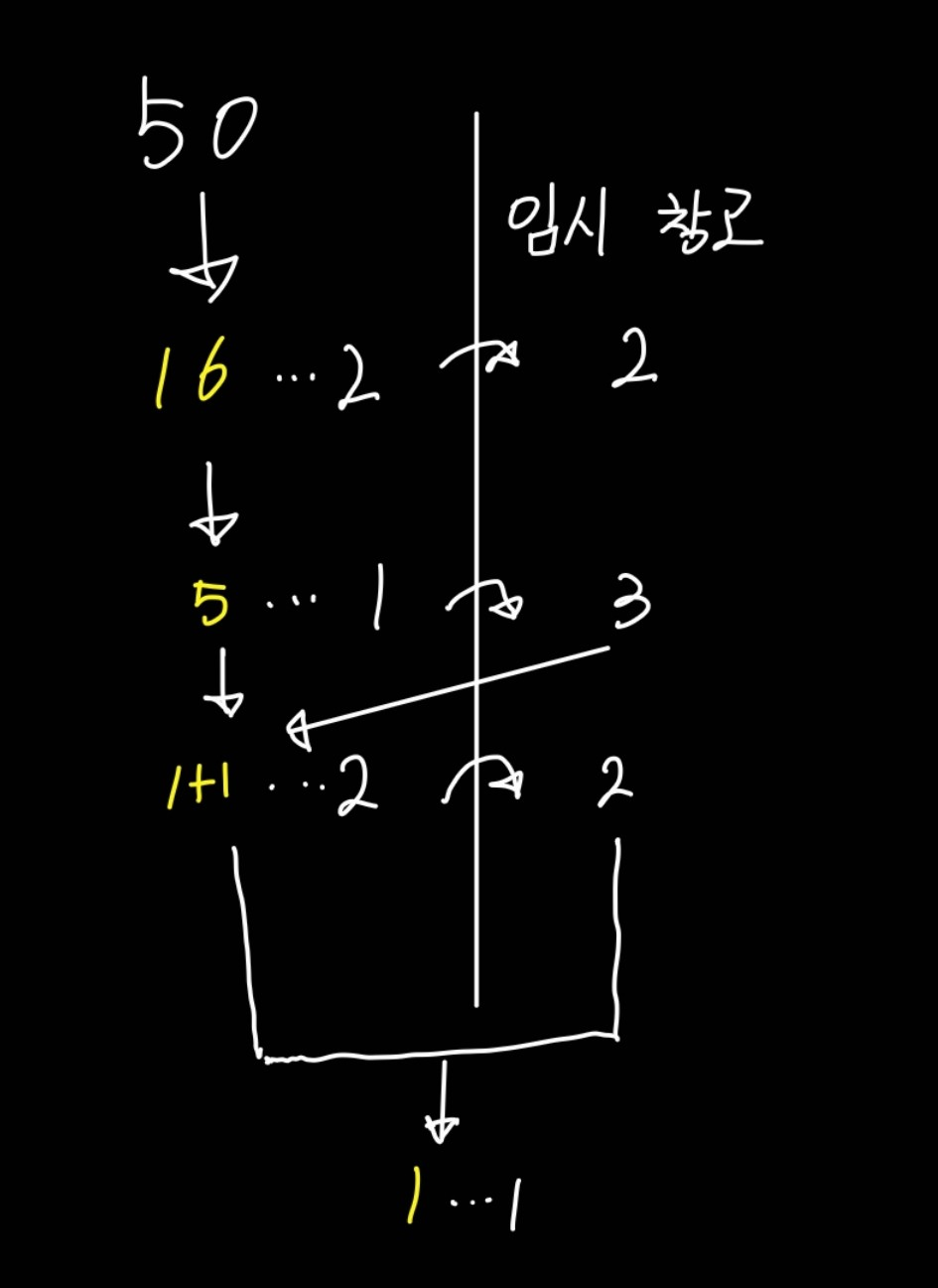
[n=50, a=3, b=1], 정답: 24

'임시 창고'에 있는 콜라들이 잠재적으로 새로운 콜라에 대한 가치가 있음을 알 수 있다.

위 그림에서 50을 3(b/a)으로 나눈 값 16.666...에서 소수점을 버리지 않고, 그대로 콜라의 개수를 포함하여, 모든 콜라에 새로운 콜라의 가치를 부여하고, 그 모든 값을 더하고, 소수점을 버린다면?

짜잔~ 새로운 콜라의 개수가!!

즉, '첫 숫자'가 n * (b / a)이고 '공비'가 b / a 인 무한 등비수열의 합을 구하고,
int로 return해서 소수점을 떨구면 된다!!!

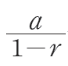
아름다운 무한 등비수열의 합 공식

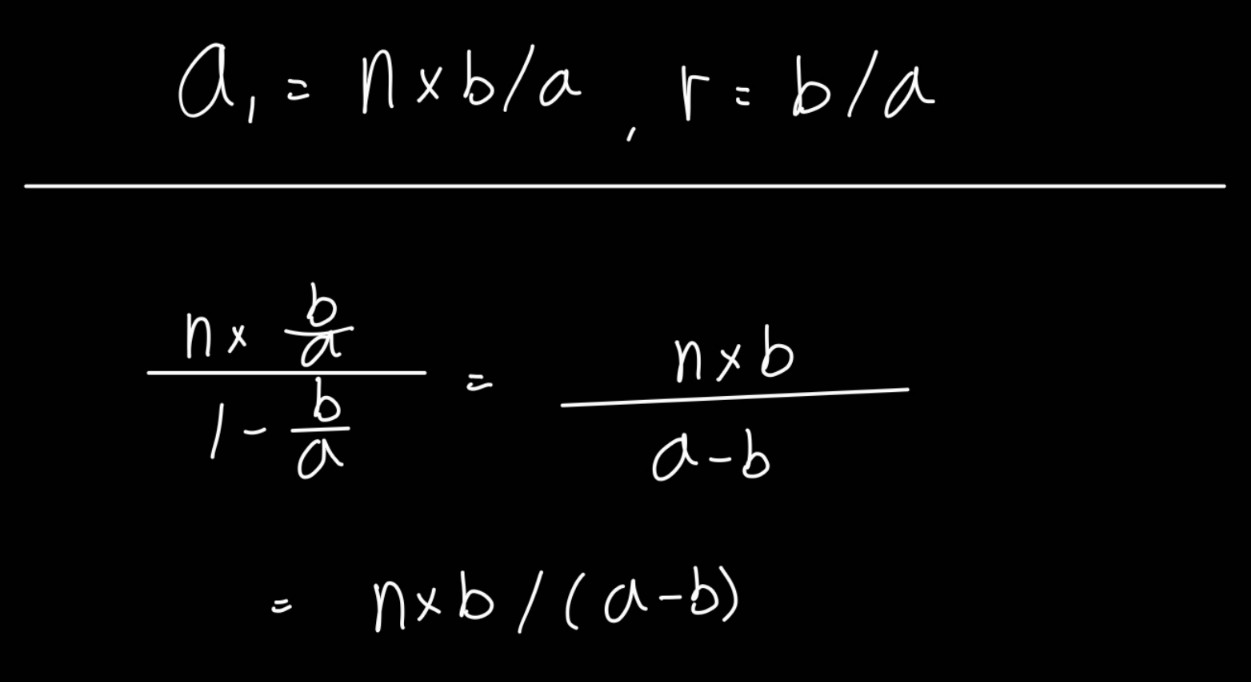
계산

저 식에 n=50, a=3, b=1을 대입해보면 25가 나온다.
정답은 24인데, 어디선가 오차가 있다...

모두 숫자가 1씩 더 크게 나온다.
한숨을 쉬며, 다른 사람의 풀이를 봤더니.. 왠걸 수식으로 푼 해답이 있다.

3. Other Solution

코드

public int otherSolution(int a, int b, int n) {
    return (n - b) / (a - b) * b;
}

감상평

이건 현대미술이다.. 아무리 고민해봐도 이해가 가지 않는다.

dOcOb

반은 해야 시작이다.

다음 포스트

[프로그래머스 / Java] 콜라 문제 #132267