[프로그래머스 / Java] 숫자 변환하기 #154538

dOcOb·2023년 1월 28일

프로그래머스

목록 보기

2/4

0. 문제 해석

x, y, n 3개의 숫자가 입력될 때, x와 n와 제한된 연산을 조합하여 최소한의 연산으로 y를 만들고, 그때 연산 횟수를 return하는 문제이다.(y를 만들 수 없다면 -1을 출력한다)
이때 사용할 수 있는 연산의 종류는 다음과 같다.

x에 n을 더한다.
x에 2를 곱한다.
x에 3을 곱한다.

Test Case

case 1
x=10, y=40, n=5, result=2
-> 10 x 2 x 2
case 2
x=10, y=40, n=30, result=1
-> 10 + 30
case 3
x=2, y=5, n=4, result=-1
-> 불가능
case 4
x=10, y=432, n=13, result=5
-> (10 + 13 + 13) x 2 x 3 x 3
case 5
x=8, y=93, n=15, result=3
-> (8 x 2 + 15) x 3

1. My Solution

이론

방정식처럼 풀 수 있을까 하며 3시간정도 고민하다가, 트리구조를 들여다보니 아이디어가 하나 떠올랐다.

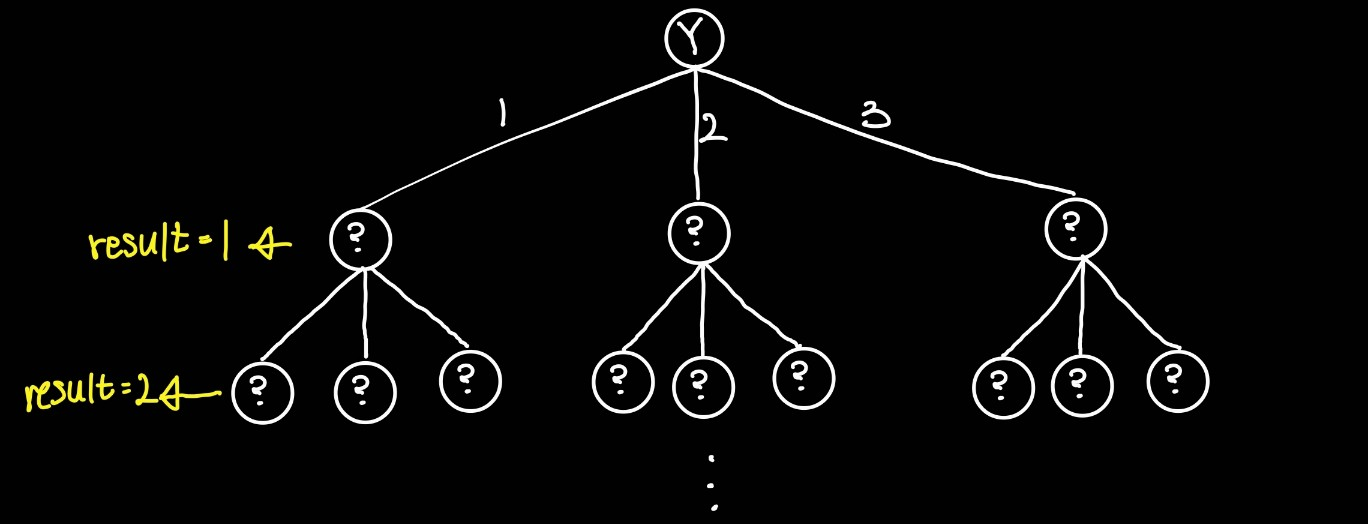
연산 선택지 1, 2, 3을 연산한 값(맞는 표현인지 모르겠지만, 이하 Node)을 모두 저장하면서
Node의 값이 y이면 result 값을 리턴한다.
이때, 저장하는 데이터의 집합체는 중복을 제거하기 위해 Set으로 하며,
Node의 값이 y보다 크면 저장하지 않는다.

코드

Solution

public int mySolution(int x, int y, int n) {

    int result = 1;
    int currentNode = x;
    Set<Integer> nodeSet = new HashSet<>();

    // 처음에 x 가 y랑 같으면 0 리턴
    if (x == y) {
        return 0;
    }

    // 처음 nodeSet 만들기
    // 연산 1
    currentNode = x + n;
    if (currentNode < y) {
        nodeSet.add(currentNode);
    } else if (currentNode == y) {
        return 1;
    }

    // 연산 2
    currentNode = x * 3;
    if (currentNode < y) {
        nodeSet.add(currentNode);
    } else if (currentNode == y) {
        return 1;
    }

    // 연산 3
    currentNode = x * 2;
    if (currentNode < y) {
        nodeSet.add(currentNode);
    } else if (currentNode == y) {
        return 1;
    }

    // nodeSet에서 node확장
    mainLoop:
    while (true) {
        result += 1;

        Set<Integer> newNodeSet = new HashSet<>();

        nodeSetLoop:
        for (int parentNode : nodeSet) {

            // 연산 1
            currentNode = parentNode + n;

            if (currentNode < y) {
                newNodeSet.add(currentNode);
            } else if (currentNode == y) {
                break mainLoop;
            }

            // 연산 2
            currentNode = parentNode * 3;

            if (currentNode < y) {
                newNodeSet.add(currentNode);
            } else if (currentNode == y) {
                break mainLoop;
            }

            // 연산 3
            currentNode = parentNode * 2;

            if (currentNode < y) {
                newNodeSet.add(currentNode);
            } else if (currentNode == y) {
                break mainLoop;
            }

        }

        // 새로 생긴 노드가 없다면 -1을 리턴
        if (newNodeSet.size() == 0) {
            return -1;
        }

        // nodeSet 최신화
        nodeSet = newNodeSet;
    }

    return result;
}