[논문] MAmmoTH: Building Math Generalist Models through Hybrid Instruction Tuning

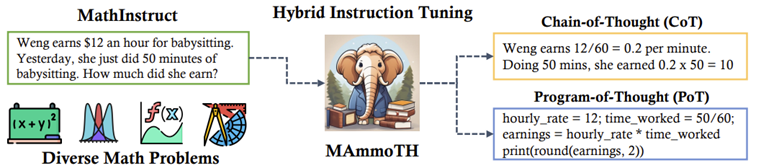
• MAmmoTH: 수학 문제 해결에 특화된 LLM. Instruction tuning dataset인 MathInstruct를 기반으로 학습
• MathInstruct: 13개의 수학 데이터 세트에서 중간 수준의 추론으로 컴파일되며, 이 중 6개는 유니티에서 새롭게 큐레이팅한 추론이 포함
• chain-of-thought(CoT)와 program-of-thought(PoT) hybrid를 제시하며 다양한 분야의 수학 다룸
  <결론>
• MAmmoTH는 9개의 수학적 추론 데이터 세트에서 평균 13%에서 29%의 정확도 향상으로 기존 오픈소스 모델을 크게 능가. MATH에서 MAmmoTH-7B은 35%에 도달하여 WizardMath-7B을 25% 능가, MAmmoTH-34B 모델은 MATH에서 46%의 정확도를 달성하여 GPT4의 CoT 결과를 뛰어넘음.
• 즉, 수학 문제 해결 모델은 다양한 분야의 문제와 hybrid 이론의 사용이 중요

Broad Coverage of Different Math Fields and Complexity Levels

• 널리 채택되고 다양한 수학 분야와 복잡성 수준을 포괄하는 몇 가지 고품질 데이터 세트(예: GSM8K, MATH, AQuA, Camel, TheoremQA)로 선택
• 기존 데이터 세트에는 추상 대수학이나 형식 논리 등 대학 수준의 수학 지식이 부족하다는 사실을 발견
• GPT-4를 사용하여 TheoremQA의 질문에 대한 CoT 근거를 합성하고 온라인에서 찾은 몇 가지 seed를 활용하여 Self-Instruct를 통해 question-CoT 쌍 생성
  Hybrid CoT and PoT Rationales
• CoT와 PoT hybird는 데이터 세트의 다양성을 향상시켜 다양한 수학 문제 해결 접근 방식 충족
• 기존의 데이터에는 CoT와 PoT 데이터 불균형 존재
• GPT-4를 활용하여 MATH, AQuA, GSM8K, TheoremQA 등 일부 데이터 PoT 근거를 보완

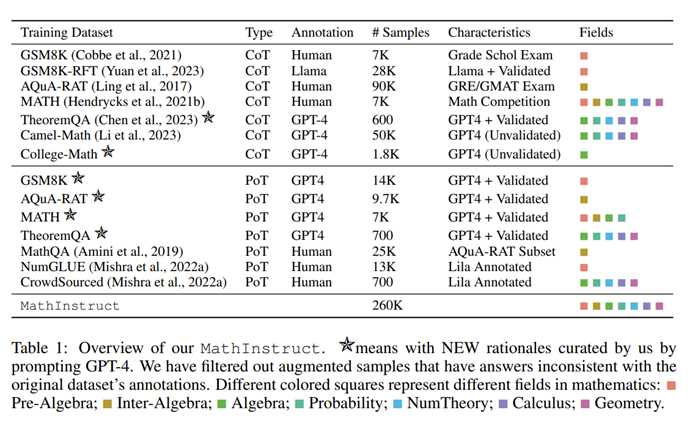
• 실행 결과를 사람이 주석을 단 실측 자료와 비교하여 GPT-4로 합성된 프로그램을 필터링하여 추가된 근거의 높은 품질을 보장.
• CoT 및 PoT이 포함된 다양한 수학 분야 (instruction, response) 260K쌍.
  언어와 난이도에서 데이터의 다양성 제공. 높은 품질과 독특한 특성을 증명.
• 데이터 구조: Alpaca instruction dataset

Llama-2 7B를 기반으로 한 MathInstruct의 다양한 주요 하위 집합의 영향. G: GSM8K, M: MATH, C: Camel, A: AQuA. "기존 데이터": 당사가 큐레이팅한 모든 새로운 근거를 제외한 표 1의 MathInstruct의 하위 집합입니다. 공간을 절약하기 위해 Mathematics는 Mat, SimulEq는 Sim, NumGLUE는 NumG, SVAMP는 SVA로 줄였습니다.

한계

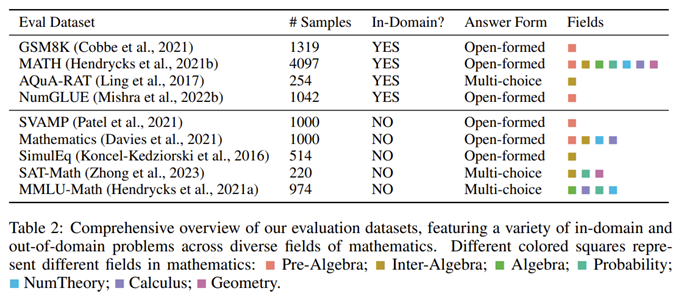
• 수학 분석, 복잡도 분석, 그래프 이론, 수치 분석 등과 같은 주요 전문 영역을 벗어난 문제에 직면했을 때 한계
• 증명형 문제에 대한 학습이 이루어지지 않았기 때문에 정리 증명 능력에도 한계 존재
  => 더 많은 분야와 정리 증명형 문제를 다룰 수 있도록 모델 확장 필요
• 수학 이외의 질문에 대한 답을 요구할 경우, MAmmoTH 모델이 잠재적으로 유해하거나 모욕적이거나 편향된 콘텐츠를 생성할 위험 존재
• 추론에서 “sycophancy”과 “Clever Hans effect”를 확인 → 사용자의 터무니없이 잘못된 주장과 비판에 의해 추론 과제에 대한 진실한 해답을 유지할 수 없다는 것
  => 이를 해결하기 위해 합성 데이터 개입 방법을 탐색 필요