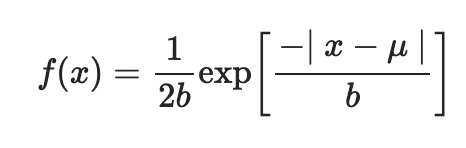1. 라플라스 분포란

- 정규 분포와 매우 흡사하게 생겼지만, 둥근 종 모양이 아니라 뾰족한 산맥처럼 생김

• 가우시안 정규분포와 비교해보면 매우 흡사한 걸 알 수 있다. 범위도 -inf<x<inf로 동일하다.

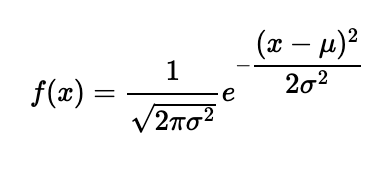
기댓값과 분산

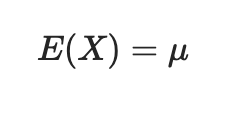
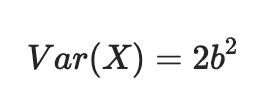
2. 그렇다면 라플라스 변환은?

- 사실 라플라스 분포와는 전혀 상관이 없다.

피에르 시몽 라플라스(Laplace)는 프랑스의 뉴턴이라고 불릴만큼 대단한 학문적 성취를 이루었다. 그는 라플라스 방정식, 라플라스 분포, 구면 조화 함수 등등을 남겼다.

라플라스의 이름을 따서 라플라스 분포와 라플라스 방정식이라고 지었을 뿐, 서로 상관은 없다.

그리고 사실 라플라스 분포보다는 라플라스 방정식이 더 유명하다. 기회가 된다면 수많은 공대생을 절망에 빠뜨린 라플라스 방정식도 포스팅을 해보겠다.

번외

라플라스 정리

중심극한정리(CLT)를 이항분포에 적용시킨 정리다.

• 확률변수 X가 이항분포 B(n,p)를 따르고, n이 충분히 클 때 (n>=50)에는
  변수 X는 근사적으로 정규분포 N(np, npq)를 따른다.
• 수식으로 보면 익숙한 중심극한정리를 발견할 수 있다.
  

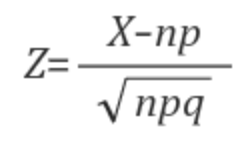
그래도 라플라스 정리는 라플라스 분포와 좀 관련이 있다.