머신러닝이란?

머신러닝이란?

머신러닝(Machine Learning)은 인공지능의 분야의 하나로써 기존 컴퓨터 시스템이 미리 정해 놓은 알고리즘에 따라서 작동하는 것과 다르게 기계 스스로 패턴 및 추론을 거쳐 작업을 할 수 있는 알고리즘 및 통계 모델과 관련한 연구입니다. 예를 들어, 알고리즘을 이용하여 자동적으로 해당 메일이 스팸 메일인지 아닌지 구분 혹은 예측할 수 있게 만드는 것이다.

규칙을 일일이 프로그래밍하지 않아도, 자동으로 데이터에서의 규칙을 학습하는 알고리즘을 연구하는 분야이다. 머신러닝은 통계학과 깊은 관련이 있으며, 대표적인 머신러닝 라이브러리는 사이킷런(scikit-learn)이다.

어떤 생선인지 분류하기

위에서 머신러닝은 기계 스스로 추론을 거쳐 구분 혹은 예측할 수 있다 하였다.
한번 생선의 길이와 무게의 데이터를 이용하여, 해당 생선이 어떤 생선인지 구분하는 법을 만들어 보자.

해당 생선 데이터는 캐글(Kaggle)에 공개된 데이터셋이다.
Kaggle/fish-market

어떤 전문가가 도미의 길이는 30cm이상이라고 알려주었다. 그래서 프로그래밍을 다음과 같이 하였다. if fish_length >= 30: print("도미")
하지만 30cm보다 큰 생선이 무조건 도미라고 말할 수 없다. 물론 고래와 새우처럼 크기의 차이가 명확하게 있다면, 길이를 기준으로 새우인지 고래인지 분류하는 프로그램을 만들 수 있다. 하지만 다음의 가정이 아니라면 무조건적인 기준을 정하기에는 어려움이 있다.

보통 프로그램은 '누군가 정해준 기준대로의 일'을 한다. 하지만 머신러닝은 누구도 알려주지 않는 기준을 자기 스스로 찾아서 일을 한다. 다시 말해 누가 기준을 정해주지 않아도 머신러닝은 30~40cm 길이의 생선은 도미이다. 라는 기준을 본인 스스로 찾을 수 있다. 머신러닝은 이러한 기준을 찾을 뿐만 아니라 해당 생선이 도미인지 아닌지 판별할 수도 있다.

이제 데이터를 이용하여 도미인지 아닌지 머신러닝을 이용하여 판별해보자.

#도미의 길이(cm)
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 31.5, 32.0, 32.0, 32.0, 
33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]

#도미의 무게(g)
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 500.0, 340.0, 600.0, 600.0, 
700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]

다음과 같이 총 35마리의 도미에 대한 데이터셋이 있다. 각 도미의 특징을 길이와 무게로 표현한 것인데, 이런 특징을 피쳐(feature)라 한다.

해당 데이터셋을 matplotlib의 산점도(scatter)을 이용하여 확인하자.

import matplotlib.pyplot as plt

plt.scatter(bream_length, bream_weight)
plt.xlabel('length')
plt.ylabel('weight')

plt.show()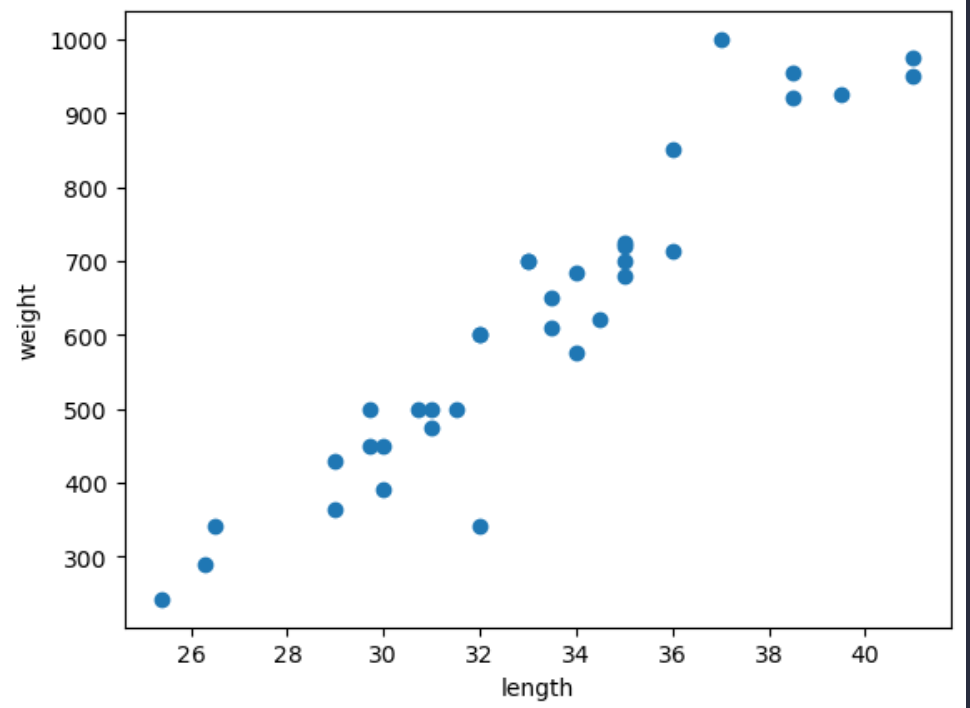

이제 또다른 생선인 빙어가 있다. 총 14마리의 빙어에 대한 데이터셋이다.

#빙어의 길이(cm)
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]

#빙어의 무게(g)
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

데이터를 한 눈에 봐도 도미와 비교했을 때 길이와 무게가 상당히 작은 것으로 보인다.
위의 도미와 비교하기 위해 두 개의 데이터를 산점도(scatter)에 한 번에 띄워보자.

plt.scatter(bream_length, bream_weight)
plt.scatter(smelt_length, smelt_weight)
plt.xlabel('length')
plt.ylabel('weight')

plt.show()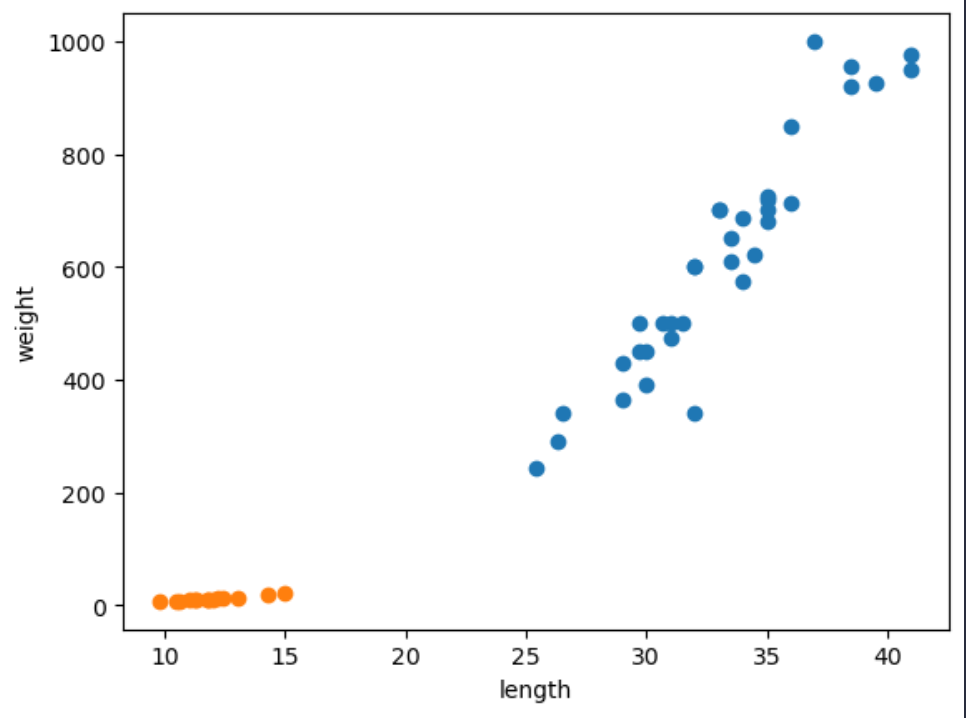

주황색 점이 빙어이고, 파란색점이 도미이다.
빙어는 길이가 늘어나도 무게의 변화가 거의 없는 것으로 보이고
도미는 길이가 늘어남에 무게도 비례하여 늘어나는 것으로 보인다.

데이터셋 준비는 완료가 됐고, 이제 이 데이터셋을 분류하기 위한 알고리즘을 정해야 한다.
가장 간단하고 이해하기 쉬운 k-최근접 이웃 알고리즘을 사용하여 어떤 생선인지 구분해볼 것이다.

k-최근접 이웃 알고리즘이란?

• K-최근접 이웃 (K-Nearest Neighbor) 알고리즘은 지도학습 알고리즘 중 하나입니다.
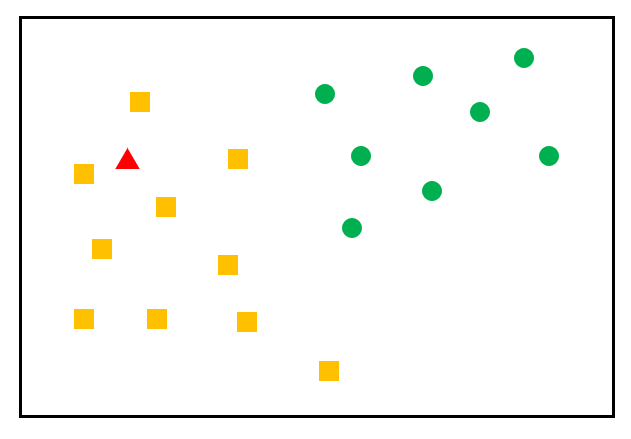
• 새로운 데이터를 입력 받았을 때, 해당 데이터와 가장 가까이에 있는 k개의 데이터를 확인해, 새로운 데이터의 특성을 파악하는 방법입니다.
• 새로운 데이터인 빨간 세모는 노란 네모와 근접해있으므로, 노란 네모가 된다.

우선 도미와 빙어의 데이터를 하나의 데이터로 합쳐준다.

length = bream_length + smelt_length
weight = bream_weight + smelt_weight

우리는 이제 머신러닝의 대표적인 패키지 사이킷런을 사용할 것이다. 이 패키지를 사용하기 위해서는 2차원 리스트로 만들어야 한다.

도미와 빙어를 합친 데이터 length, weight를 합쳐 2차원 리스트로 생성하자.

fish_data = [[l,w] for l,w in zip(length, weight)]

총 생선 49마리의 길이와 무게의 데이터를 모두 준비했다. 마지막으로 준비할 데이터는 정답 데이터이다. 즉 첫 번째 생선은 도미, 두 번째 생선은 빙어라는 식으로 해당 데이터가 어떤 생선의 데이터인지 답을 만드는 것이다.

정답 데이터를 만드는 이유는?
머신러닝 알고리즘은 생선의 길이와 무게를 보고 도미와 빙어인지 구분하는 규칙을 찾아야 한다. 그렇게 하려면 해당 길이와 무게를 가진 생선이 도미인지 빙어인지 알려주어야 한다.
머신러닝은 물론, 컴퓨터 프로그램은 우리가 쓰는 문자(자연어)를 직접 이해하지 못한다. 그렇기 때문에 대신해서 도미와 방어를 1과 0으로 표현을 한다.

49개의 데이터 중 앞의 35개의 데이터는 도미, 뒤에 14개의 데이터는 빙어에 대한 데이터이다. 이에 대한 정답 데이터를 곱셈 연산자를 이용하여 만들어주자.

#도미는 1, 빙어는 0으로

fish_target = [1] * 35 + [0] * 14
print(fish_target)

출력 결과물 => [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

이제 사이킷런 패키지의 k-최근접 이웃 알고리즘의 클래스 KKNeighborsClassifer를 import 후 객체를 생성한다.

from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()

현재 우리가 구한 데이터셋은 총 2개가 있다.

• 생선의 길이와 무게에 대한 2차원 리스트
• 생선이 도미인지 빙어인지 알려주는 리스트

이 2개의 데이터를 해당 객체에 전달하여 데이터에 대한 규칙을 학습시킨다.
이 과정을 머신러닝에서는 훈련(training)이라 한다.

kn.fit(fish_data, fish_target)

이제 kn이라는 모델은 49개의 데이터 fish_data와 fish_target으로 학습이 되었다.
이제 이 학습된 객체가 얼마나 잘 훈련이 되었는지 평가해보겠다.

kn.score(fish_data, fish_target)
#출력 결과: 1.0

해당 값은 0과 1사이의 값을 반환한다. 1은 모든 데이터를 정확하게 맞췄단 뜻이며 0.5는 절반만 맞췄다는 뜻이다. 해당 결과는 1.0이 나왔으며 이는 모든 답을 정확하게 맞췄단 뜻이다. 이 값을 정확도(Accuracy)라 한다.

이제 새로운 생선에 대한 데이터를 직접 만들어 도미인지 빙어인지 분류를 해볼까요?

길이가 30cm, 무게가 600g인 생선이 있다. 이 생선을 산점도에 띄어보면 녹색 세모점과 같다.

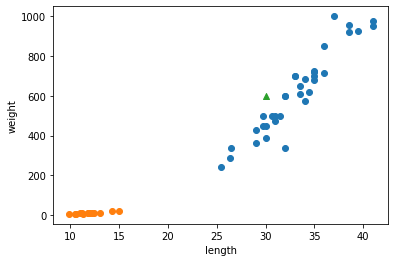
녹색 세모점에 해당하는 생선은 도미와 빙어 중 무엇일까?
아마 직관적으로는 이 삼각형은 도미라고 판단할 것이다. 왜냐하면 삼각형 주변에 다른 도미의 데이터가 많기 때문이다. k-최근접 이웃 알고리즘도 마찬가지이다. 한번 실제로 확인해보자.

kn.predict([[30, 600]])
#출력 결과물: array([1])

predict()라는 메서드는 새로운 데이터에 대한 정답을 예측한다. 앞에서의 메서드 fit()과 마찬가지로 2차원 리스트로 전달해야 한다.
반환값은 1이며 우리는 도미를 1, 빙어는 0으로 가정하였다. 즉 녹색 삼각형에 대한 생선은 도미이다.

k-최근점 이웃 알고리즘은 근접해있는 데이터를 참고하여 해당 데이터가 도미인지 빙어인지 구분한다고 하였다. 그렇다면 몇개의 데이터를 참고할까?

사이킷런의 KNeighborsClassifier의 Default값은 5이다. 이 기준은 n_neighbors라는 매개변수로 바꿀 수 있다. 예를 들어 다음과 같이 하면 어떤 결과가 나올까?

kn49 = KNeighborsClassifier(n_neighbors=49)

이 의미는 가장 가까운 49개의 데이터를 참고한다는 뜻이다. 즉 우리는 49개의 데이터 fish_data를 가지고 학습을 시켰으므로 fish_data에 있는 모든 생선을 참고하여 예측하게 된다.

다시 말하면 fish_data에 있는 49개의 데이터 중 35개의 도미가 대다수를 차지하고 있기 때문에 어떤 데이터를 넣어도 무조건 도미로 예측을 할 것이다.

이렇기 때문에 적절한 n_neighbors의 수를 이용해야 한다.

k-최근접 이웃 알고리즘에 대한 장단점
장점:

• 단순하기 때문에 다른 알고리즘에 비해 구현하기가 쉽다
• 훈련 데이터를 그대로 가지고 있어 특별한 훈련을 하지 않기 때문에 훈련 단계가 매우 빠르게 수행된다.

단점:

• 모델을 생성하지 않기 때문에 특징과 클래스 간 관계를 이해하는데 제한적이다. 모델의 결과를 가지고 해석하는 것이 아니라, 미리 변수와 클래스 간의 관계를 파악하여 이를 알고리즘에 적용해야 원하는 결과를 얻을 수 있기 때문이다
• 훈련 단계가 빠른 대신 데이터가 많아지면 분류 단계가 느리다.