데브코스 34일차 - 데이터 모델링 (1)

kiki·2024년 4월 4일

데브코스 데이터분석

데브코스

목록 보기

10/17

키워드

데이터 모델링, 회귀분석

데이터 모델링이란?

주어진 데이터에서 사용하고자 하는 x(feature, input, 독립변수), 알고싶은 값 y(label, output, 종속변수)이 있을 때 y=f(x)라는 함수를 통해서 x와 y의 관계를 설명할 수 있다면?
y와 x의 관계를 효과적으로 설명하는 f() 함수를 만드는 일
- y 값이 존재할 때 → supervised learning
- y 값이 존재하지 않는 경우 unsupervised learning
- y값이 연속형인 경우 regression task
- y 값이 categorical 값인 경우 classification task
Bayes theorem의 관점
- 조건부 확률: 어떤 사건이 일어났다는 ‘전제 하에’ 다른 사건이 일어날 확률
  - P(B|A) = P(A∩B)/P(A), P(A|B) = P(B∩A)/P(B) ⇒ P(B|A) = P(A|B)P(B) / P(A)
  - 데이터 모델링 관점에선 P(세타|X) = P(X|세타)P(세타)/P(X)
    - X는 관측된 데이터, 세타는 데이터에 대한 가설, 즉 모델의 파라미터 값을 의미한다.
    - P(세타)는 데이터 관측 이전의 파라미터의 확률 분포를 의미. 보통 모든 값에 대한 확률이 동일하다고 가정
    - P(X|세타)는 likelihood, 즉 파라미터가 주어졌을 때 X데이터가 관측될 확률 분포
    - P(세타|X)는 X가 주어졌을 때 파라미터의 확률 분포
  - 궁극적인 목적은 P(세타|X)를 최대화하는 세타를 찾는 것
    - P(세타)가 일정하다는 가정 하에 P(X|세타)(likelihood)를 최대화하는 세타를 추정(MLE)
    - 그렇지 않을 때는 P(X|세타)P(세타)를 최대화 하는 세타를 추정(MAP)
    
    ⇒ 이게 데이터 모델링이다..
데이터 모델링 과정
- 데이터 전처리 및 간단한 분석(통계적 분석, 시각화 등)
- training set/test set으로 분리 (validation set도 나누기도 함)
- training set으로 사용할 모델을 학습 (model.fit(training_set))
- 학습된 모델의 test set에 대한 예측값을 통해 모델의 성능을 평가 (실제값과 예측값의 비교)
- 새로운 데이터에 대해 학습된 모델을 이용해 y 값을 예측 (추론)

선형회귀 (Linear Regression)

x와 y 간에 선형의 관계가 있다고 가정할 때 주로 사용됨 (y=wx + b)
- 예측값 y와 실제 y가 최대한 가까워지는 w와 b 값을 찾도록 학습됨

선형회귀의 가정
- 오차항(엡실론)의 기대치는 0이다
- 오차항은 일정한 분산을 가진다
- i≠j일 때, 엡실론 i와 엡실론 j는 서로 독립이다.
- 독립변수 X와 엡실론은 서로 독립이다.
- 엡실론은 정규분포 N(0, 시그마^2)를 따른다.
가정
- 회귀 모형은 선형성을 가진다.
  - E(Y) = E(b+wX+엡실론) = b+wX+E(엡실론) ⇒ b+wX
- 종속변수 Y의 분산은 일정한 값을 갖는다.
- 엡실론 i와 엡실론 j는 서로 독립이며, 엡실론은 자기상관성이 없다.
  - 시계열 데이터의 경우는 자기상관성이 존재할 수 있다.
- Y는 정규분포를 따른다.
  - E(Y) = b+wX, Var(Y) = 시그마^2
  - Y~N(b+wX, 시그마^2)
비용함수
- 실제 Y와 Ypred의 오차를 계산하는 식을 세우고, 이 오차를 최소화하는 w,b를 찾아야함
- 오차에 대한 식을 손실함수, 비용함수, 목적함수 라고 한다. (조금씩 차이가 있음)
- 선형회귀에선 Residual sum of squares(RSS), 혹은 Mean squared error(MSE)를 사용
  - mse: 오차(예측-실제) 제곱의 합의 평균
- 비용함수가 미분가능하고 아래로 볼록할 때, cost의 최저점은 비용함수를 w와 b로 각각 편미분 했을 때 0이 되는 지점
Ordinary Least Squares (최소제곱법)
- 오차 엡실론을 최소화하는 w,b를 추정하는 방법
Gradient descent (경사하강법)
- 최적화(정답과 예측값의 차이를 최소화하는 네트워크 구조의 파라미터를 찾는 과정) 방법
- 변수가 많아지거나 비용함수가 복잡해지는 경우 최소 제곱법을 통해 한번에 loss가 최소인 파라미터를 추정하기 어려워짐
- 이 경우, 파라미터에 대해서 비용함수를 편미분한 값(gradient)을 learning rate만큼 여러번 업데이트 해주는 것을 경사하강법이라고 한다.
  - 모든 학습 데이터에 대해 한번에 gradient descent step을 계산하는 batch gradient descent보다는 매 스텝에서 미니배치만큼의 데이터를 샘플링 해서 학습하는 mini-batch stochastic gradient descent(SGD) 방식으로 학습한다.

Ridge, Lasso

overfitting (과적합)
- 학습 데이터에 과하게 fitting 되는 경우를 의미
- 테스트 셋에서의 로스가 증가. 즉 일반화되지 못한 상태를 의미
- 데이터에 내재된 복잡도보다 모델의 복잡도가 더 과한 경우, 데이터셋 사이즈가 작은 경우
- 선형 회귀에선, 고려하는 변수가 많아질수록 과적합이 발생할 가능성이 높아짐
Generalization (일반화)
- 학습할 때와 추론할 때의 성능 차이가 많이 나지 않는 경우. 즉 모델이 여러 추론 상황에서 잘 쓰일 수 있음을 의미
오버피팅 해결 방법
- 모델의 복잡도 줄이기
  - 모델이 가질 수 있는 파라미터를 줄이기
  - 모델이 고려하는 피쳐 중 상대적으로 중요한 피쳐들만 모델의 인풋으로 사용해볼 수 있다.
- 정규화
  - 모델이 가지는 복잡도를 제한하는 방법
  - 모델의 파라미터가 가지는 값의 크기를 cost function에 추가해주는 방식으로 파라미터 값의 크기를 제한한다. (파라미터를 cost function에 추가해 해당 파라미터를 조절하도록)
Ridge regression
- 선형 최귀 모델에 L2 loss를 추가해서 파라미터를 정규화해줌
- 람다(하이퍼파라미터) 값을 조절해 패널티를 조절
- sklearn.linear_model에서 ridge를 import해서 linearRegression과 동일하게 사용
Lasso
- 위의 ridge 식에서 패널티의 sum에 베타의 절댓값을 사용

로지스틱 회귀, SVM

로지스틱 회귀
- 회귀가 아닌 분류 task에서 사용되는 모델
- y에 시그모이드를 적용해 y의 값이 0~1 사이 값이 되도록 만든다.
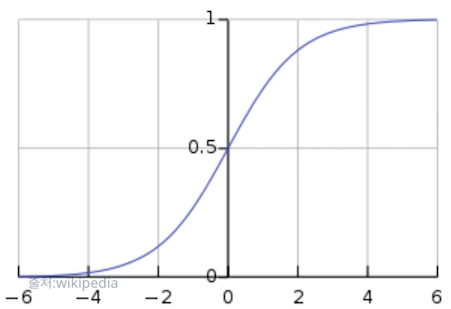
- 0 이상의 인풋에 대해 0.5 이상의 값을 내고, 0 이하의 인풋에 대해선 0.5 이하의 값을 반환
SVM (Support Vector Machine)
- 어느정도 허용 오차(C) 안에 있는 오차값은 허용해준다! (+-엡실론 범위 안에 있는 값에 대해선 loss를 계산하지 않는다.)
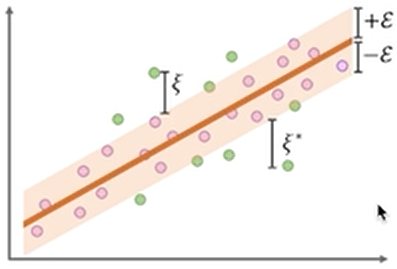
- 허용오차 값 C를 잘 설정해야 모델이 좋은 성능을 낼 수 있다.
- SVR은 regression task, SVC는 classification task에서 사용

Random forest

decision tree
- x를 기준삼아, ‘해당 기준을 만족/불만족시 y 값이 ~값일 것이다’라는 조건(x)-결과(y)를 나무처럼 발전시킴
- classification에선 y가 클래스, regression에선 y값이 평균값
랜덤 포레스트
- decision tree를 무작위로 여러개를 만든 후 각 트리마다 나온 decision들을 voting(ensemble)해 최종적인 y 값을 예측
- 파라미터
  - n_estimators(트리 개수)
  - max_depth(각 트리의 길이)
  - 무조건 트리 개수나 길이 값이 크다고 성능이 좋아지진 않으며, 학습 시간이나 차지하는 메모리가 지나치게 커질 수 있다.
- 데이터셋이 작은 경우엔, 최적화가 잘 된 랜덤포레스트 모델이 성능이 좋음

모르는 것

손실함수(비용함수)를 편미분한 값이 뭐더라
- 기울기
  - 미분 가능한 N개의 다변수 함수 f를 각 축이 가리키는 방향마다 편미분한 것
  - 즉 축이 x,y로 두개라면 x로 편미분한 값, y로 편미분한 값
- 즉 기울기가 0이되는(낮아지는) 지점을 찾아 감
편미분한 값에 learning rate를 곱한 만큼 파라미터를 조정하는건가?
- 가중치의 경우, Wn = Wn-1 - lr*(손실함수 편미분 값)으로 계산됨
- 즉 학습률로 가중치를 얼마나 변경할지(step size, 가중치를 업데이트 하는 과정을 step이라고 함) 선택할 수 있는거다. 이렇게 수정하면서, 손실함수의 값이 거의 변하지 않을 때까지 가중치를 업데이트하는 과정을 반복
- 그래서 편미분값에 -를 붙여 기울기가 양수면 왼쪽(-)으로, 기울기가 음수면 오른쪽(+)이 되는쪽으로 가중치를 업데이트해 손실함수가 최소값을 갖도록 하는 것
- 그러면 손실함수를 각 파라미터로 편미분한 값으로 각 파라미터를 업데이트하는건가?
  - 어 맞음… 그니까 여기선 가중치 W를 갖고 설명한 것 처럼, 만약 내가 업데이트하고자 하는 파라미터 X가 있을 때 손실함수를 X에 대해 편미분한 값을 파라미터 X를 업데이트하는 데 사용하고자 하는거지
    $θnew=θold−α∇L(θold)$
  - 근데 그럴려면 손실함수에 세타(파라미터)가 포함되어있어야하는거 아니야?
    - 아 파라미터가 가중치랑 편향이잖슴. 근데 손실함수에 예측값이 들어가는 데 그 예측값이 wx+b니까 파라미터가 손실함수에도 포함되는 거임
모든 학습 데이터에 대해 한번에 gradient descent step을 계산하는 batch gradient descent보다는 매 스텝에서 미니배치만큼의 데이터를 샘플링 해서 학습하는 mini-batch stochastic gradient descent(SGD) 방식으로 학습한다.
- 배치마다 하지 않고 배치 내에서 쪼개서 한다는 말인가?
  - 그니까, 경사하강법(BGD)은 한 번의 가중치 업데이트에 모든 데이터를 사용하므로 1 batch의 사이즈가 전체 데이터 크기라고 할 수 있음
    - 하지만 배치 경사하강법을 사용하면, 가중치 업데이트에 연산량이 많아지고 메모리 소비가 심해 시간이 오래 걸린다는 단점이 있음 ⇒ 결국 성능 저하로 이어짐
  - 그래서 SGD는 전체 데이터 대신 랜덤하게 하나의 데이터를 뽑아 한 번의 반복당 한개의 데이터를 이용해 가중치를 업데이트하는 방법이다.
    - 하지만 이는 하나의 데이터만 사용하기 때문에 최적값에 수렴하지 않을 가능성이 있어 수렴 안정성이 낮고 진폭이 매우 크다.
  - 그래서 나온 절충안이 미니배치 경사하강법(MSGD)임, 배치의 크기를 사용자가 정해 업데이트에 사용하는 방법. 즉 전체 데이터를 미리 정한 배치 사이즈만큼씩 묶어 각 묶음에 대해 경사 하강법을 적용대신 일부 데이터 모음(mini-batch)를 사용해 loss를 계산한다는 것
    - BGD보다는 연산량이 적고, SGD보다는 안정적으로 수렴한다는 장점이 있다.
  - 참조
- 스텝이랑 배치랑 무슨 차이였지
  - 배치는 데이터를 배치 사이즈로 묶은 그룹을 의미하는 말
  - 스텝은 그 배치 내의 데이터에 대해 기울기를 계산해 파라미터를 업데이트 하는 과정을 말한다. (텐서플로우에서는 이를 iteration이라고 하기도 함)
SVM이 그래서 무슨 역할을 하는거지?
- 주로 2개의 값 분류(이진 분류)를 위해 사용 (확률(Y)을 1,0으로 변환해 사용, threshold를 지정)
- x가 0보다 크면 긍정, 0보다 작으면 부정을 의미
- 나의 경우 모델 output을 0~1사이 값으로 변경해 확률로 사용했었다.
- 선형으로 나타낼 때보다 유한 결정?을 낼 수 있음
- 근데 이걸 분류모델로 사용한다고?
  - 만약에 분류하는 직선인 선형 모델의 경우 좀더 retricted한 분류가 될 것이다. 이를 SVM을 사용해 해결하고자 하고, 학습을 통해 그래프의 feature들을 조정해 높은 정확도의 분류 라인을 만들어내는 것이다. 참고
SVM 이미지에서 초록색이 서포트 벡터래, 뭐지?
- support vector가 선과 가장 가까운 포인트를 말한다고 함. SVM은 오차 범위의 포인트까지 포함이니 오차범위 바깥의 가장 가까운 포인트를 의미하는 거겠지.
- 즉 서포트벡터와의 거리, 즉 Margin이 최대화(분리를 명확하게) 되는 것이 robustness를 최대화할 수 있는 것이라고 한다.